-
1、如图,线段的垂直平分线相交于点O.求证: .

-
2、如图,在中,是斜边的垂直平分线,连接 , 若 , 则度.

-
3、如图,已知是等边三角形,于点 , 于点 , 若 , 则 .

-
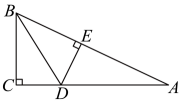
4、如图,在中, , , 点为边上一点,连接 , 过点作于点 , 且 , 则的度数为 .
-
5、如图,已知 , 补充一个条件 , 则可使得

-
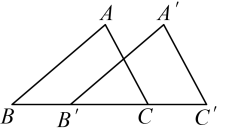
6、如图所示,将沿所在的直线平移到的位置,则 , 图中与 , 与 , 与是对应角.
-
7、已知是的中线,若与的周长分别为 , , 则 .
-
8、在中, , 则的度数为( )A、 B、 C、 D、
-
9、如图,在中, , , 则的长为( )
 A、4 B、6 C、3 D、5
A、4 B、6 C、3 D、5 -
10、在中, , 以为圆心,适当长为半径画弧,交于两点,再分别以为圆心,大于的长为半径画弧,两弧交于点 . 作射线交于点 , 若 , 则点到的距离为( )
 A、3 B、4 C、 D、5
A、3 B、4 C、 D、5 -
11、如图,在中, , 线段的垂直平分线交于点E,交于点D,则的周长为( )
 A、21 B、14 C、13 D、9
A、21 B、14 C、13 D、9 -
12、如图,在中,于点D,E是上一点,若 , , , 则的周长为( )
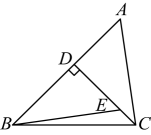 A、24 B、23 C、22 D、26
A、24 B、23 C、22 D、26 -
13、已知图中的两个三角形全等,则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、某校准备在如图所示的三角形空地上种植花卉,需将其分成面积相等的两块分别种植牡丹和芍药,小敏作出线段来划分,那么是的( )
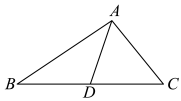 A、角平分线 B、中线 C、高线 D、以上都不是
A、角平分线 B、中线 C、高线 D、以上都不是 -
15、下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
16、“滴滴”司机李师傅周日上午在南北方向的江门大道上营运,共连续运载十批乘客,若规定向北为正,李师傅营运十批乘客里程如下:(单位:千米)(1)、将最后一批乘客送到目的地时,李师傅距离第一批乘客出发地的南面还是北面?距离出发地多少千米?(2)、若汽车每千米耗油升,则汽车共耗油多少升?(3)、若“滴滴”的收费标准为:起步价11元(不超过3千米),超过3千米,超过部分每千米2元.则李师傅在上午一共收入多少元?
-
17、我市旅游局发布统计报告:国庆期间,瘦西湖风景区在7天假期中每天接待游客的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数).
日期
10月1日
10月2日
10月3日
10月4日
10月5日
10月6日
10月7日
人数变化单位:万人
若9月30日的游客人数为万人,
(1)、国庆期间瘦西湖风景区一共接待游客多少万人?(2)、若门票为每人100元,那么国庆期间瘦西湖风景区门票收入是多少万元? -
18、在计算两个数减法: , 由于不小心,减数被墨水污染;(1)、嘉淇误将后面的“”看成了“”,从而算得结果为 , 请求出被墨水污染的减数;(2)、请你正确计算此道题.
-
19、根据题意计算求值(1)、若 , , 且 ,求的值.(2)、若 , 求的值.
-
20、一只蚂蚁从某点P出发在一条直线上来回爬行,假定向右爬行的路程为主,向左爬行的路程记为负,爬行的各段路程一次为(单位:厘米): , , , , , ,(1)、蚂蚁共爬行了多少厘米?(2)、若蚂蚁共用了9分钟完成上面的路程,蚂蚁的速度是多少?