-
1、下列各组数中,互为倒数的是( )A、5与 B、与 C、与 D、与
-
2、下列整式中,是单项式且次数是8的是( )A、 B、 C、 D、
-
3、下列有理数中,绝对值最小的是( )A、9 B、 C、7 D、
-
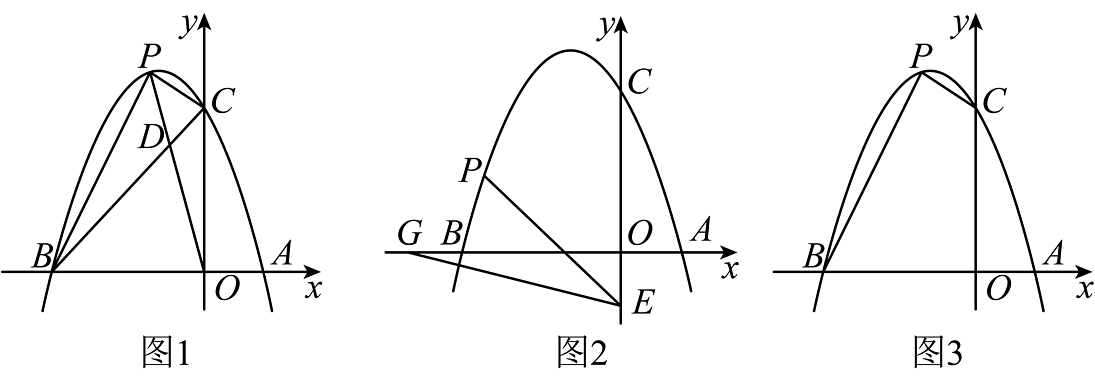
4、已知抛物线y=ax2+bx+3经过点A(1,0)和点B(﹣3,0),与y轴交于点C,点P为第二象限内抛物线上的动点.
(1)抛物线的解析式为 , 抛物线的顶点坐标为 ;
(2)如图1,连接OP交BC于点D,当S△CPD:S△BPD=1:2时,请求出点D的坐标;
(3)如图2,点E的坐标为(0,﹣1),点G为x轴负半轴上的一点,∠OGE=15°,连接PE,若∠PEG=2∠OGE,请求出点P的坐标;
(4)如图3,是否存在点P,使四边形BOCP的面积为8?若存在,请求出点P的坐标;若不存在,请说明理由.
-
5、如图,四边形是正方形,点O为对角线的中点.
 (1)、问题解决:如图①,连接 , 分别取的中点P,Q,连接 , 则与的数量关系是_____,位置关系是_____;(2)、问题探究:如图②,是将图①中的绕点A按顺时针方向旋转得到的三角形,连接 , 点P为的中点,连接并延长交于F, , . 证明;(3)、拓展延伸:如图③,是将图①中的绕点按逆时针方向旋转得到的三角形,连接 , 点 , 分别为 , 的中点,连接 , . 若正方形的边长为1,求的面积.
(1)、问题解决:如图①,连接 , 分别取的中点P,Q,连接 , 则与的数量关系是_____,位置关系是_____;(2)、问题探究:如图②,是将图①中的绕点A按顺时针方向旋转得到的三角形,连接 , 点P为的中点,连接并延长交于F, , . 证明;(3)、拓展延伸:如图③,是将图①中的绕点按逆时针方向旋转得到的三角形,连接 , 点 , 分别为 , 的中点,连接 , . 若正方形的边长为1,求的面积. -
6、阅读以下材料,并解决相应问题:
小明在课外学习时遇到这样一个问题:
定义:如果二次函数( , , 是常数)与( , , , 是常数)满足 , , , 则这两个函数互为“旋转函数”.求函数的旋转函数.小明是这样思考的,由函数可知, , , , 根据 , , , 求出 , , 就能确定这个函数的旋转函数.
请思考小明的方法解决下面问题:
(1)写出函数的旋转函数
(2)若函数与互为旋转函数,求的值.
(3)已知函数的图象与x轴交于A,B两点(点A在点B的右边),与y轴交于点C,点A,B,C关于原点的对称点分别是 , , , 试求证:经过点 , , 的二次函数与互为“旋转函数”.
-
7、两段相互垂直的墙AB和AC的长分别为12m和3m,用一段长为23m的篱笆成一个矩形菜园(篱笆全部使用完),如图所示,矩形菜园的一边AD由墙AC和一节篱笆CD构成,一边AF靠在墙AB上,一边EF上有一个2m的门.假设篱笆CD的长为xm,矩形菜园的面积为 , 回答下面的问题:
 (1)、用含x的式子表示篱笆DE的长为m,x的取值范围是;(2)、菜园的最大面积是多少?求出此时x的值是多少?
(1)、用含x的式子表示篱笆DE的长为m,x的取值范围是;(2)、菜园的最大面积是多少?求出此时x的值是多少? -
8、已知关于x的一元二次方程x2+(2m﹣1)x+m2﹣3=0有实数根.(1)、求实数m的取值范围;(2)、当m=2时,方程的根为x1 , x2 , 求代数式(x12+2x1)(x22+4x2+2)的值.
-
9、如图,在平面直角坐标系中,的顶点坐标为 . (画图时字母应标注清楚)
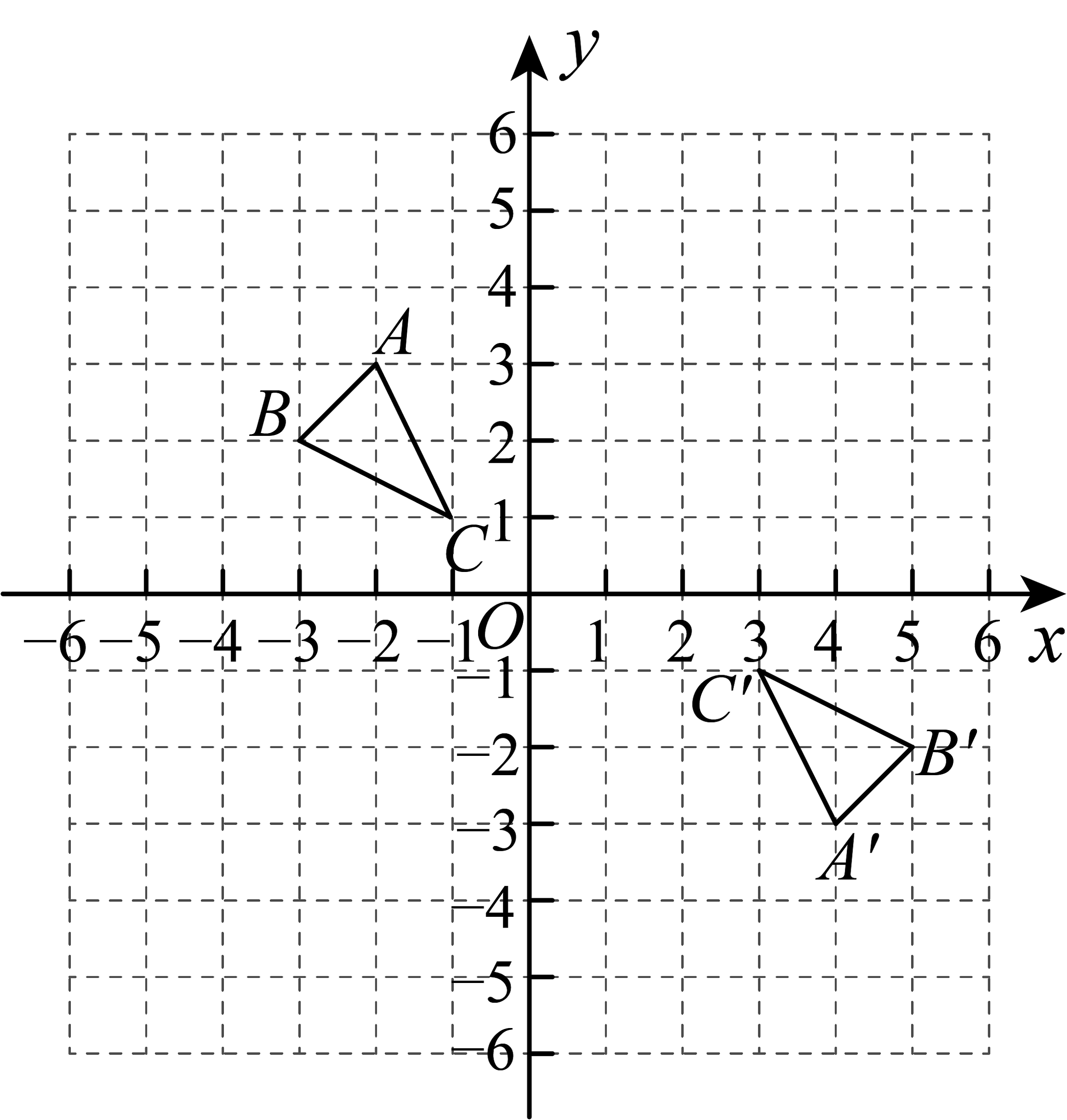 (1)、将绕原点O顺时针旋转 , 请画出旋转后的;(2)、画出绕原点O旋转后得到的;(3)、若与关于某点中心对称,则对称中心的坐标为_______.
(1)、将绕原点O顺时针旋转 , 请画出旋转后的;(2)、画出绕原点O旋转后得到的;(3)、若与关于某点中心对称,则对称中心的坐标为_______. -
10、如图,点A是抛物线对称轴上的一点,连接OA,以A为旋转中心将AO逆时针旋转90°得到AO' , 当O'恰好落在抛物线上时,点A的坐标为 .

-
11、函数与的图象如图所示,有以下结论:①;②;③;④当时, . 其中正确的是( )
 A、①④ B、③④ C、①②③ D、②④
A、①④ B、③④ C、①②③ D、②④ -
12、如图,在平面直角坐标系中,将边长为1的正方形绕点O顺时针旋转后得到正方形 , 依此方式,绕点O连续旋转次得到正方形 , 那么点的坐标是( )
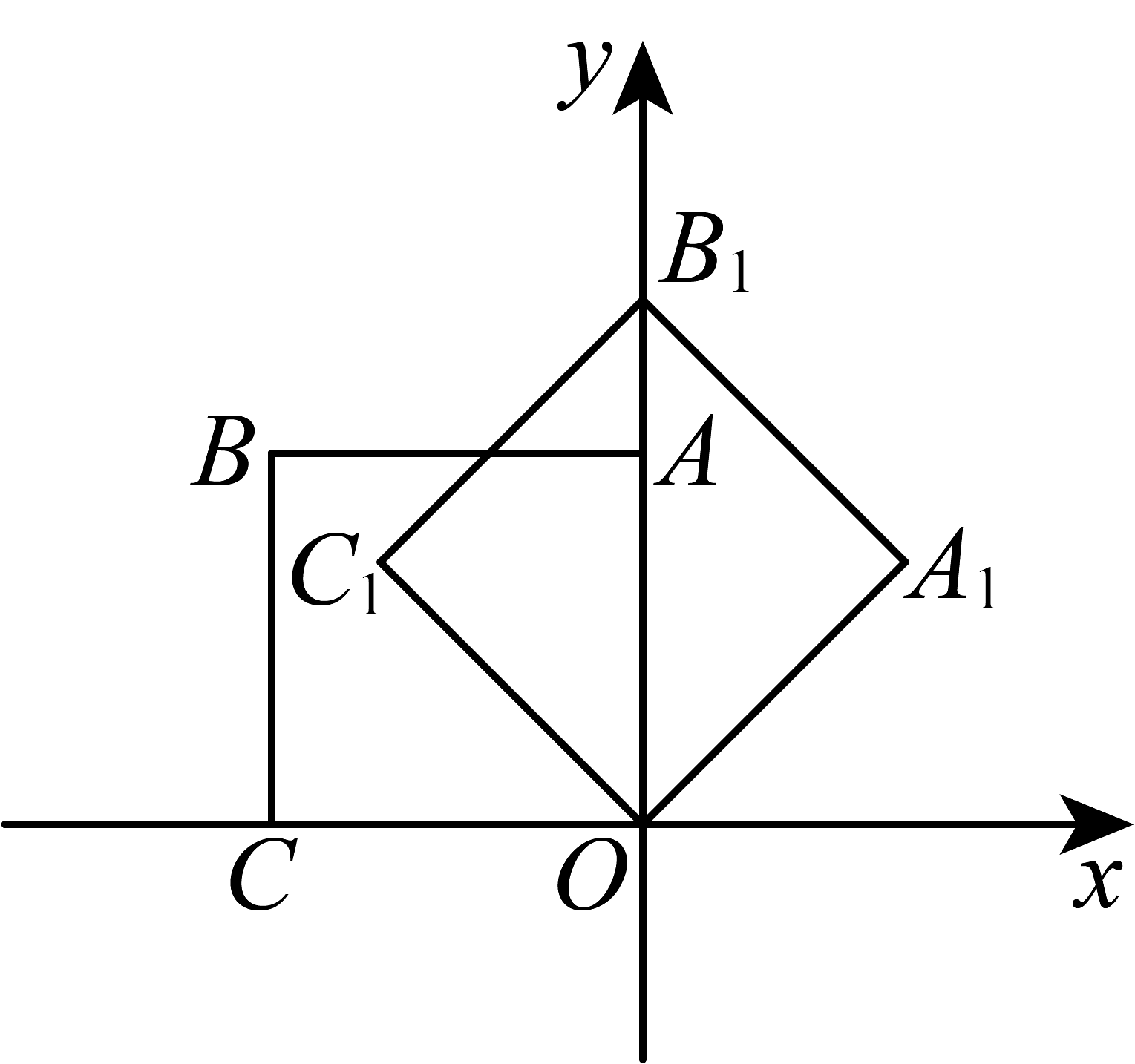 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,P是等边三角形ABC内的一点,且PA=3,PB=4,PC=5,将△ABP绕点B顺时针旋转60°到△CBQ位置.连接PQ,则以下结论错误的是( )
 A、∠QPB=60° B、∠PQC=90° C、∠APB=150° D、∠APC=135°
A、∠QPB=60° B、∠PQC=90° C、∠APB=150° D、∠APC=135° -
14、如图,在中, , 将绕点A顺时针旋转旋转后的对应点分别是和 , 连接 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
15、已知点A(1,y1),B(4,y2),C(﹣3,y3)均在抛物线y=2x2﹣4x+m上,下列说法中正确的是( )A、y3<y2<y1 B、y2<y1<y3 C、y3<y1<y2 D、y1<y2<y3
-
16、方程的一个实数根为 , 则的值是( )A、2022 B、2021 C、2020 D、2019
-
17、抛物线的顶点坐标是( )A、 B、 C、 D、
-
18、掷实心球是某地区中考体育考试的选考项目,已知一名男生第一次投实心球行进路线是一条抛物线,行进高度与水平距离之间的函数关系如图所示,掷出时起点处高度为 , 当水平距离为时实心球行进至最高点处.
 (1)、求这名男生第一次投实心球的抛物线的解析式;(2)、根据该地区2023年中考体育考试评分标准(男生),投掷过程中,实心球从起点到落地点的水平距离不小于 , 此项目考试满分为15分.按此评分标准,该生在此项考试中是否得满分,请说明理由.(3)、该男生第二次投掷时,实心球运动的竖直高度与水平距离近似满足函数关系 . 则第二次投掷时出手点与着陆点的水平距离为多少?
(1)、求这名男生第一次投实心球的抛物线的解析式;(2)、根据该地区2023年中考体育考试评分标准(男生),投掷过程中,实心球从起点到落地点的水平距离不小于 , 此项目考试满分为15分.按此评分标准,该生在此项考试中是否得满分,请说明理由.(3)、该男生第二次投掷时,实心球运动的竖直高度与水平距离近似满足函数关系 . 则第二次投掷时出手点与着陆点的水平距离为多少? -
19、我国水资源比较缺乏,人均水量约为世界人均水量的四分之一,其中西北地区缺水尤为严重.一村民为了蓄水,他把一块矩形白铁皮四个角各切去一个同样大小的小正方形后制作一个无盖水箱用于接雨水.已知白铁皮的长为280cm,宽为160cm(如图).
(1)若水箱的底面积为16000cm2 , 请求出切去的小正方形边长;
(2)对(1)中的水箱,若盛满水,这时水量是多少升?(注:1升水=1000cm3水)

-
20、如图,在平面直角坐标系中,三个顶点的坐标分别为 , , .
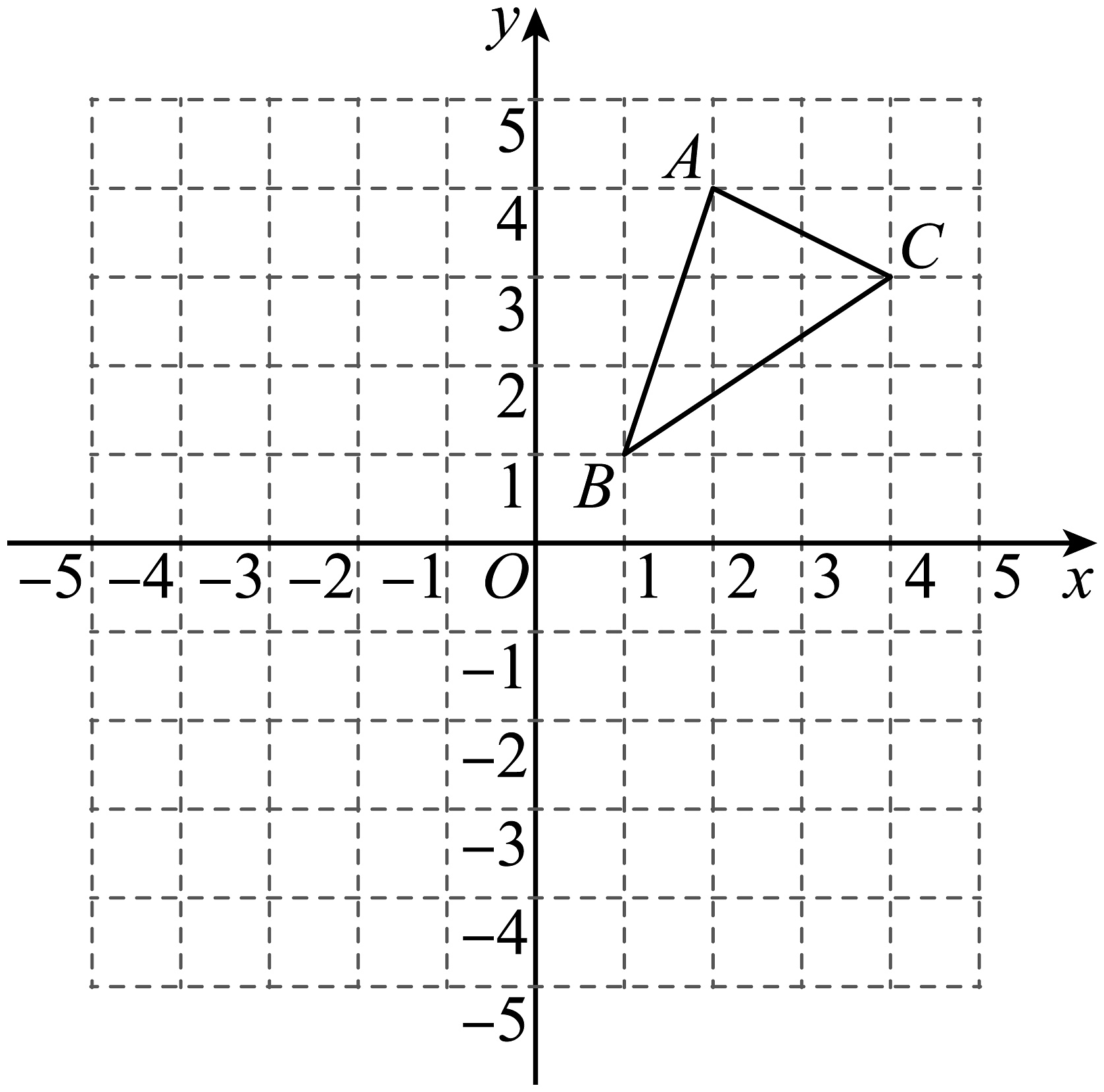 (1)、请画出与关于原点成中心对称的图形(、、的对应点分别为、、),并写出、、的坐标;(2)、若以点为旋转中心逆时针旋转后得到的图形为(、、的对应点分别为、、),在网格中画出旋转后的图形,并写出、、的坐标.
(1)、请画出与关于原点成中心对称的图形(、、的对应点分别为、、),并写出、、的坐标;(2)、若以点为旋转中心逆时针旋转后得到的图形为(、、的对应点分别为、、),在网格中画出旋转后的图形,并写出、、的坐标.