-
1、如图,为的直径,过圆上一点D作的切线交的延长线于点C,过点O作交于点E,连接 .
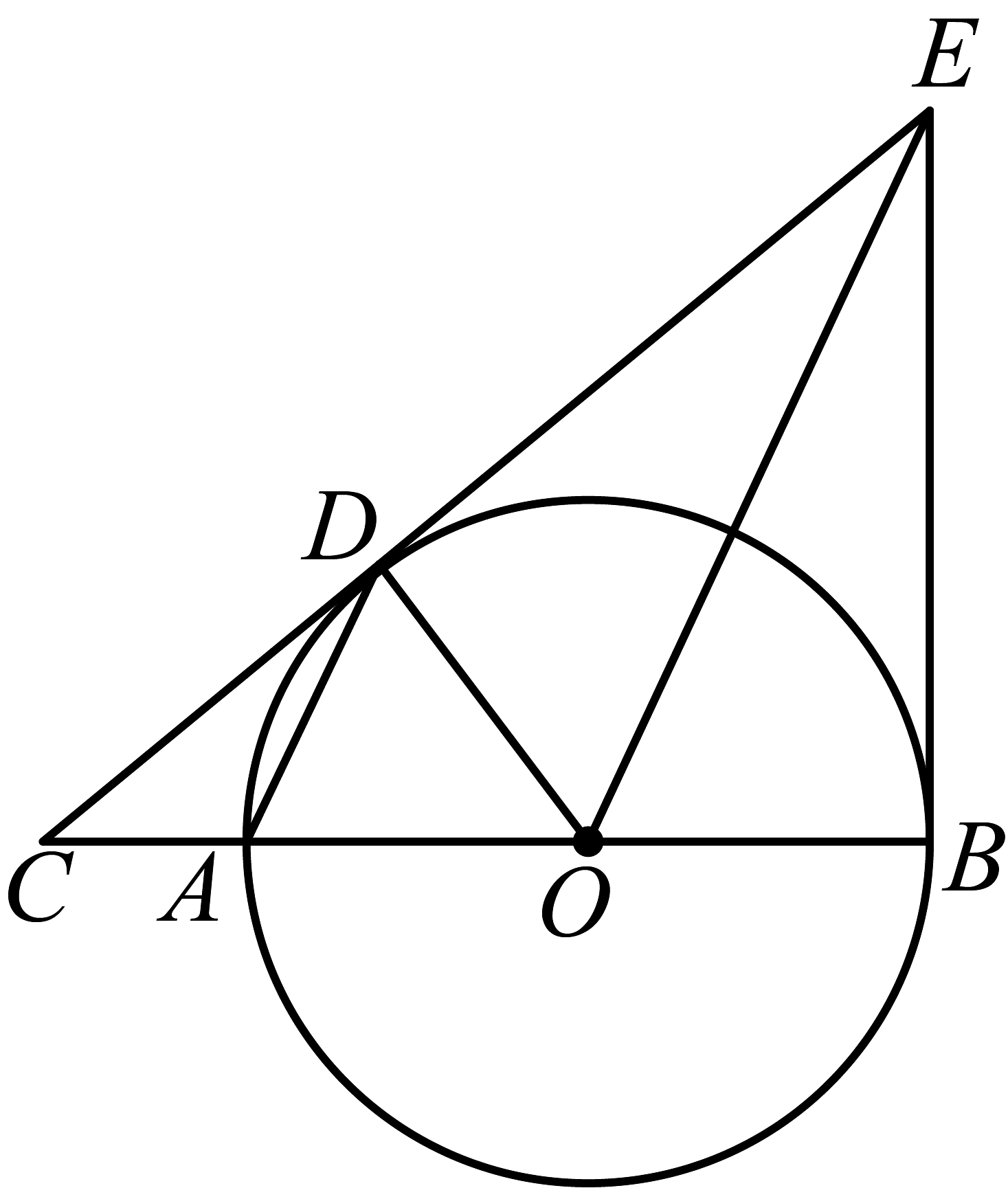 (1)、求证:直线是的切线;(2)、若 , , 求的半径及的长.
(1)、求证:直线是的切线;(2)、若 , , 求的半径及的长. -
2、解下列方程:(1)、(2)、
-
3、若抛物线向左平移1个单位长度,向下平移2个单位长度,则所得的抛物线的解析式是 .
-
4、如图,将绕点逆时针旋转得到 , 若点在线段的延长线上, , 则旋转角的度数为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、如图,一个底部呈球形的烧瓶,球的半径 , 瓶内液体的最大深度 , 则截面圆中弦的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如图所示,A是上一点,且 , , , 则与的位置关系是( )
 A、相离 B、相切 C、相交 D、相割
A、相离 B、相切 C、相交 D、相割 -
7、对于二次函数的图象,下列说法正确的是( )A、开口向上 B、对称轴是直线 C、当时,y随x的增大而增大 D、顶点坐标为
-
8、已知抛物线的顶点为D,与轴交于A,B两点(A在B左边),与y轴交于点C
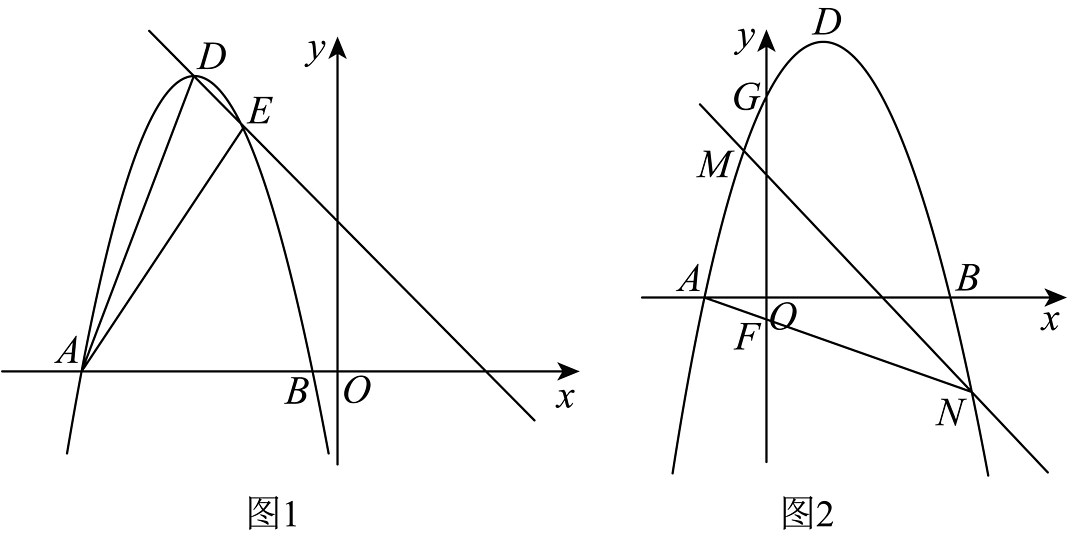 (1)、若点A坐标为 , 点C坐标为求其解析式;(2)、如图(1),已知抛物线的顶点D在直线:上滑动,且与直线交于另一点E,若的面积为 , 求此时点A的坐标;(3)、如图(2),在(1)的条件下,直线交抛物线于M,N两个不同的点,直线分别交y轴于点G、F,求与满足的数量关系.
(1)、若点A坐标为 , 点C坐标为求其解析式;(2)、如图(1),已知抛物线的顶点D在直线:上滑动,且与直线交于另一点E,若的面积为 , 求此时点A的坐标;(3)、如图(2),在(1)的条件下,直线交抛物线于M,N两个不同的点,直线分别交y轴于点G、F,求与满足的数量关系. -
9、如图,在平面内将绕点逆时针旋转至 , 使 , 如果 , 那么旋转角度.

-
10、不透明袋子中有红球10个,黄球20个,还有一些蓝球,这些球除颜色外无其他差别,从袋子里随机摸出一个恰好是黄球的概率为 , 则蓝球有( )A、30个 B、60个 C、40个 D、20个
-
11、点关于原点对称的点的坐标是( )A、 B、 C、 D、
-
12、计算:(1)、;(2)、 .
-
13、已知 , 则 .
-
14、已知:在中,为的平分线.求证: .

-
15、已知二次函数(是常数).(1)、若该二次函数图象与轴没有交点,求的取值范围;(2)、若该二次函数图象与轴的其中一个交点坐标为 , 求一元二次方程的解.
-
16、如图,D是的边上的一点, , , , 求证: .

-
17、如图,已知二次函数的图像分别经过点 , , 求该函数的解析式.

-
18、如图,抛物线过点A、、 , 点为抛物线在第四象限部分上的一点,则面积的最大值为

-
19、已知 , 且 , 则
-
20、二次函数的顶点坐标为