-
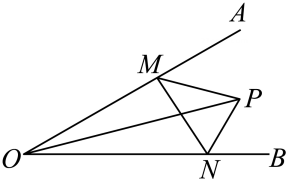
1、如图所示,∠AOB=30°,点M,N分别是射线OB,OA上的动点,点P为∠AOB内一点,且OP=4,则△PMN周长的最小值为.
-
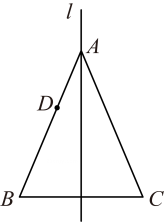
2、如图所示,在等腰三角形ABC中,AB=AC=10,S△ABC=24,l是△ABC的对称轴,D是AB上一动点,在l上存在一点P,能使PB+PD的值最小,这个最小值为.
-
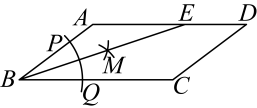
3、如图所示,在四边形ABCD中,AD∥BC,AB=6,AD=10.以点B为圆心,任意长为半径作弧,分别交BA,BC于点P,Q;再分别以P,Q为圆心,大于PQ的长为半径作弧,两弧在∠ABC内交于点M.连接BM并延长,交AD于点E,则DE的长为.
-
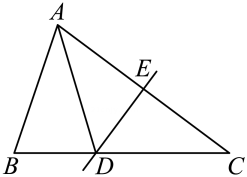
4、如图所示,在△ABC中,AC的垂直平分线交BC于点D,交AC于点E,∠B=∠ADB.若AB=4,则DC的长是.
-
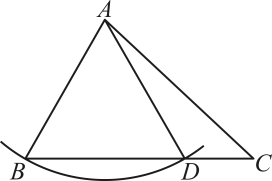
5、如图所示,在△ABC中,以点A为圆心,线段AB的长为半径画弧,交BC于点D,连接AD.若AB=5,则AD的长为.
-
6、小明在纸上画了一个边长为5 cm的等边三角形ABC,并将一把宽为2 cm的直尺按如图所示方式放在所画的△ABC上,使得直尺一条边与△ABC的边BC在同一条直线上,另一条边交边AB于点E,则AE=cm.

-
7、等腰三角形的一个内角是120°,则它的底角是.
-
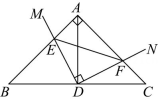
8、如图所示,在Rt△ABC中,∠B=45°,AB=AC,D为BC中点,直角∠MDN绕点D旋转,DM,DN分别与边AB,AC交于E,F两点,有下列结论:
①△DEF是等腰直角三角形;②AE=CF;③△BDE≌△ADF;④BE+CF=EF.其中正确结论的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
9、如图所示,在△ABC中,∠ACB=90°,AC<BC.分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于D,E两点,直线DE交BC于点F,连接AF.以点A为圆心,AF长为半径画弧,交BC延长线于点H,连接AH.若BC=3,则△AFH的周长为( )
 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6 -
10、如图所示,在Rt△ABC中,∠ACB=90°,根据尺规作图的痕迹判断,以下结论错误的是( )
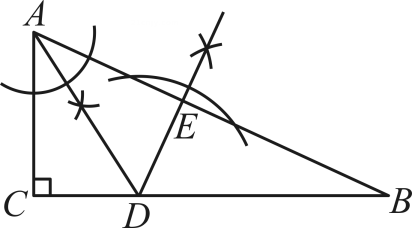 A、∠BDE=∠BAC B、∠BAD=∠B C、DE=DC D、AE=AC
A、∠BDE=∠BAC B、∠BAD=∠B C、DE=DC D、AE=AC -
11、如图所示,在△ABC中,∠C=90°,DE是AB的垂直平分线,DE=4,∠B=30°,则BC等于( )
 A、12 B、10 C、8 D、6
A、12 B、10 C、8 D、6 -
12、在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的位置是△ABC的( )A、三边中线的交点处 B、三条角平分线的交点处 C、三边垂直平分线的交点处 D、三边上高所在直线的交点处
-
13、如图所示,AD平分∠BAC,交BC于点D,DE⊥AB于点E,DF⊥AC于点F.若S△ABC=12,DF=2,AC=3,则AB的长是( )
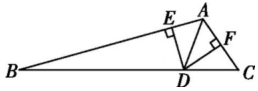 A、2 B、4 C、7 D、9
A、2 B、4 C、7 D、9 -
14、四边形ABCD的边长如图所示,∠BAD=90°,∠ABC=120°,E为边AD上一动点(不与A,D两点重合),连接BE,将△ABE沿直线BE折叠,点A的对应点为点F,则点C与点F之间的距离不可能是( )
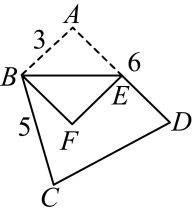
A、3 B、4 C、5 D、8 -
15、将一张正方形纸片按如图所示的步骤,通过折叠得到图④,在CA,CB上各取一点连成虚线,沿该虚线剪去一个角,剩余部分展开铺平后得到的图形可能是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
16、下列说法正确的是( )A、等腰三角形的对称轴是底边的中线 B、等腰三角形顶角的平分线是它的一条对称轴 C、等腰三角形任意两个角相等 D、三角形的三条高所在的直线一定交于一点
-
17、下列四种图案中,可以看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、一个小立方体的六个面分别标有字母A,B,C,D,E,F,从三个不同方向看到的情形如图所示.
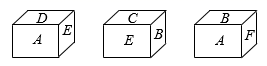 (1)、A对面的字母是 , B对面的字母是 , E对面的字母是.(请直接填写答案)(2)、若A=2x-1,B=-3x+9,C=-7,D=1,E=2x+5,F= -9,且字母E与它对面的字母表示的数互为相反数,求A,B的值.
(1)、A对面的字母是 , B对面的字母是 , E对面的字母是.(请直接填写答案)(2)、若A=2x-1,B=-3x+9,C=-7,D=1,E=2x+5,F= -9,且字母E与它对面的字母表示的数互为相反数,求A,B的值. -
19、若一个棱柱有18个顶点,且所有侧棱长的和为45cm,则每条侧棱长为cm.
-
20、爱乐实水果超市以每箱元的价格从水果批发市场购进箱橘子,若以每箱净重为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准质量的差值/kg
0
箱数
3
3
7
5
2
(1)、这箱橘子的总质量是多少?(2)、需要将橘子从批发市场送到水果超市,现有两种取货方式:方式一:批发市场送货上门,需另交元送货费;
方式二:超市雇车自取,需支付租车费和装卸费:
租车费:元
装卸费:以内(包括)元, 超出的部分元 .
请你根据计算说明超市应选择哪种取货方式,并求出箱橘子的成本.
(3)、在(2)的条件下,若水果店按获利计算出零售价,并以零售价售出一部分收回成本后,剩余的橘子全部七折销售,请计算该水果店在销售这批橘子过程中共盈利多少元?(利润率)