-
1、当三角形中一个内角β是另外一个内角α的0.5倍时，我们称此三角形为“友好三角形”，其中α是这个“友好三角形”的“友好角”.如果一个“友好三角形”中有一个内角为54°，那么这个“友好三角形”的“友好角”的度数为.
-
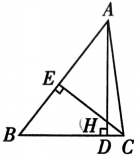
2、如图，在 中， 垂足分别是点 D，E，AD，CE 交于点 H，已知 则 .
-
3、 如图，已知∠ABC=∠DCB，添加下列条件中的一个：①∠A=∠D ②AC=DB ③AB=DC.其中不能确定的是.(填序号)
-
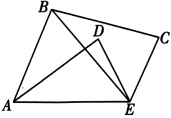
4、如图，已知 连接AB，∠ABE = 65°，∠BAD = 30°，则∠CBE 的度数为.
-
5、如图，把△ABC沿DE 折叠，当点 A 落在四边形 BCDE 内部时，则∠A 与∠1+∠2 之间有一种数量关系始终保持不变，请试着找一找这个规律，你发现的规律是 ( )
A、 B、 C、 D、 -
6、如图，四边形 ABCD 是正方形，BE⊥EF，DF⊥EF，BE=2.5cm ，DF=4 cm，那么 EF 的长为 ( )
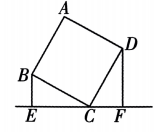A、6.5 cm B、6 cm C、5.5 cm D、4 cm -
7、如图，在△ABC和△BDE中，点C在边BD上，边AC交边BE于点F，若 AC=BD，AB=ED，BC=BE，则∠ACB等于( )
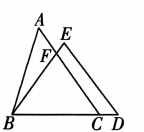A、∠EDB B、∠BED C、∠EBD D、2∠ABF -
8、如图，图1中有3个以MN为高的三角形，图2中有10个以MN为高的三角形，图3 中有21个以MN为高的三角形，…，以此类推，则图6中以MN为高的三角形的个数为 ( )
A、55 B、78 C、96 D、105 -
9、中国古代数学家刘徽在《九章算术注》中，给出了证明三角形面积公式的出入相补法.如图，在△ABC 中，分别取AB，AC的中点D，E，连接DE，过点 A 作AF⊥DE，垂足为 F，将△ABC分割后拼接成长方形 BCHG.若DE=5，AF=3，则△ABC的面积是 ( )
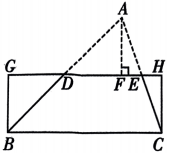A、20 B、25 C、30 D、35 -
10、如图所示，将含 45°角的直角三角板与含角的直角三角板叠放在一起，若∠1=70°，则∠2的度数为( )
A、85° B、60° C、50° D、 -
11、如图，点 D，E分别在线段AB，AC上，CD 与BE 相交于O点，已知AB=AC，添加下列条件，不能证明△ABE≌△ACD的是 ( )
A、∠B=∠C B、BE=CD C、BD=CE D、∠BDO=∠CEO -
12、如图，在△ABC 中，∠C=90°，点D在AC上，DE∥AB，若∠CDE=160°，则∠B的度数为 ( )
A、40° B、50° C、60° D、70° -
13、下列长度的3 根小木棒不能搭成三角形的是 ( )A、 B、 C、 D、
-
14、在△ABC中，∠A=36°，∠B=72°，则△ABC是 ( )A、钝角三角形 B、等腰三角形 C、等边三角形 D、等腰直角三角形
-
15、如图所示，在Rt△ABC中，∠ACB=90°，CD⊥AB于点D，∠BAC的平分线分别交BC，CD于点E，F.
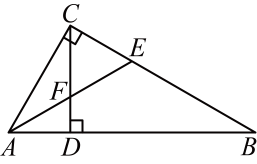
(1)、试说明：△CEF是等腰三角形；(2)、若点E恰好在线段AB的垂直平分线上，猜想线段AC与线段AB的数量关系，并说明理由；(3)、在(2)的条件下，若CE=2，AC=2.5，求△ABE的面积. -
16、观察发现：劳动人民在生产、生活中创造了很多取材简单又便于操作的方法，正如木匠师傅的“木条画直角法”.如图①所示，他用木条能快速画出一个以点A为顶点的直角，具体作法如下：
①木条的两端分别记为点M，N，先将木条的端点M与点A重合，任意摆放木条后，另一个端点N的位置记为点B，连接AB；
②木条的端点N固定在点B处，将木条绕点B顺时针旋转一定的角度，端点M的落点记为点C(点A，B，C不在同一条直线上)；
③连接CB并延长，将木条沿点C到点B的方向平移，使得端点M与点B重合，端点N在CB延长线上的落点记为点D；
④用另一根足够长的木条画线，连接AD，AC，则画出的∠DAC是直角.
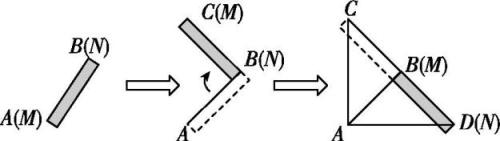
①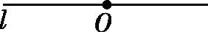
②
(1)、推理论证：如图①所示，小亮尝试揭示此操作的数学原理，请你补全横线上的依据：因为AB=BC=BD，
所以△ABC与△ABD是等腰三角形.
所以∠BCA=∠BAC，∠BDA=∠BAD.(依据1)
所以∠BCA+∠BDA=∠BAC+∠BAD=∠DAC.
因为∠DAC+∠BCA+∠BDA=180°，(依据2)
所以2∠DAC=180°.
所以∠DAC=90°.
依据1：；依据2：.
(2)、拓展探究：小亮进一步研究发现，用这种方法作直角存在一定的误差，用平时学习的尺规作图的方法可以减少误差.如图②所示，点O在直线l上，请用无刻度的直尺和圆规在图②中作出一个以O为顶点的直角，记作∠POQ，使得直角边OP在直线l上，P在O左侧，Q在直线l上方.(保留作图痕迹，不写作法) -
17、如图所示，已知在等边三角形ABC中，D是AC的中点，E是BC延长线上的一点，且CE=CD，DM⊥BC，垂足为M，试说明：M是BE的中点.
-
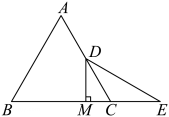
18、如图所示的是由16个小正方形组成的正方形网格图，现已将其中的两个涂黑.请你用四种不同的方法分别在下图中再涂黑三个空白的小正方形，使整个图形成为轴对称图形.
-
19、如图所示，已知∠ADC+∠ABC=180°，DC=BC.
试说明：点C在∠DAB的平分线上.
-
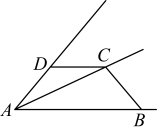
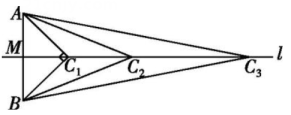
20、如图所示，直线l为线段AB的垂直平分线，交AB于点M，在直线l上取一点C1 ， 使得MC1=MB，且AC1⊥BC1 ， 得到第一个三角形ABC1；在射线MC1上取一点C2 ， 使得C1C2=BC1 ， 得到第二个三角形ABC2；在射线MC1上取一点C3 ， 使得C2C3=BC2 ， 得到第三个三角形ABC3……依次这样进行下去，则第2 024个三角形ABC2 024中，∠AC2 024B的度数为.
