-
1、已知多项式是关于x,y的六次三项式,且单项式的次数与该多项式的次数相同.(1)、求m,n的值(2)、当 , 时,求多项式的值.
-
2、已知:a,b互为相反数,c,d互为倒数,m的绝对值是3.求代数式的值.
-
3、巴中,作为一座拥有优美的自然风光、文化底蕴深厚的城市,境内有众多著名的旅游景点,吸引了众多游客慕名而来.如表是某社会实践小组统计的2024年10月1日~7日七天内巴中某景点每天旅游人数变化表(正号表示人数比前一天多,负号表示比前一天少)
日期
1日
2日
3日
4日
5日
6日
7日
人数变化单位:万人
已知该景点9月30日的游客人数为万人,根据图表,可求出10月1日的游客人数是(万人).结合以上信息解决下列问题:
(1)、10月7日该景点的旅客人数为多少万人?(2)、10月1日到7日该景点旅客人数最多的一天比最少的一天多多少万人?(3)、如果每万人带来的经济收入约为400万元,则10月1日到7日该景点的旅游总收入约为多少万元? -
4、计算(1)、;(2)、;(3)、;(4)、 .
-
5、把下列各数填入相应集合的括号内: .
整数集合:{ }
分数集合:{ }
非负数集合:{ }
-
6、如果 , 请求出的值为 .
-
7、如图是某种细胞分裂示意图,这种细胞经过1次分裂便由1个分裂成2个.根据此规律,一个细胞经过6次分裂后可分裂成个细胞.

-
8、定义一种新运算 , 求的值 .
-
9、单项式系数是 , 次数是 .
-
10、中国最早采用负数的记载可以追溯到公元前200年的《九章算术》,在《九章算术》中,负数被称为“负数”或“盈不足”,并被用于解决一些代数问题.如果把收入6元记作元,那么支出8元记作 .
-
11、下列说法中,错误的个数( )
①若 , 则;
②若 , 则有是正数;
③A、B、C三点在数轴上对应的数分别是、6、x,若相邻两点的距离相等,则;
④若代数式的值与x无关,则该代数式的值为2021;
⑤如果a、b、c是非零有理数,那么所有可能的值为 .
A、1个 B、2个 C、3个 D、4个 -
12、当时,代数式的值是10,则当时,这个代数式的值是( )A、 B、10 C、 D、12
-
13、若 , 且 , 则( )A、5或7 B、或 C、或5 D、或7
-
14、数轴上点P表示的数为 , 与点距离为4个单位长度的点表示的数为( )A、1 B、 C、1或 D、1或
-
15、某面粉厂加工的面粉袋上,标有标准质量为的字样,从中产品中任意拿出一袋称重,质量不符合标准重量的要求的是( ).A、 B、 C、 D、
-
16、若 , 则的值是( )A、 B、4 C、0 D、1
-
17、下列说法错误的是( )A、是一次三项式 B、是二次三项式 C、是五次二项式 D、是二次二项式
-
18、如图1, , 为中点,点在上方,连接 , .
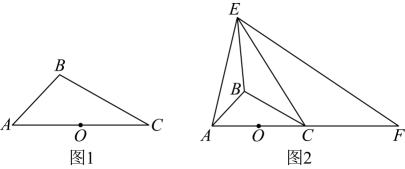 (1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .
(1)、尺规作图:作点关于点的对称点(保留作图痕迹,不写作法),连接 , , 并证明:四边形为平行四边形;(2)、如图2,延长至点 , 使得 , 当点在直线的上方运动,直线的上方有异于点的动点 , 连接 , , , , 若 , 且 .①求证:;
②的长是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
-
19、某玩转数学小组发现隧道前通常设有涉水线和限高架等安全警示,为探究其内在的数学原理,该小组考察了如图1所示的双向通行隧道.以下为该小组研究报告的部分记录,请认真阅读,解决问题.

发现问题确定目标
涉水线设置
限高架设置
数学抽象绘制图形
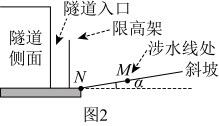
隧道及斜坡的侧面示意图,可近似如图2所示.
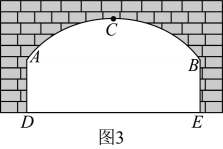
图3为隧道横截面示意图,由抛物线的一部分和矩形的三边构成.
信息收集资料整理
当隧道内积水的水深为0.27米时,(即积水达到涉水线处),车辆应避免通行.
车辆进入隧道,应在行驶车道内通行(禁止压线),且必须保证车辆顶部与隧道顶部在竖直方向的空隙不小于0.3米.
实地考察数据采集
斜坡的坡角为 , 并查得: ,
,
.
隧道的最高点C到地面距离为5.4米,两侧墙面高米,地面跨度米.车辆行驶方向的右侧车道线(宽度忽略不计)与墙面的距离为1米.
问题解决:
(1)、如图2,求涉水线离坡底的距离(精确到0.01米);(2)、在图3中建立适当的平面直角坐标系,求抛物线的解析式;(3)、限高架上标有警示语“车辆限高h米”(即最大安全限高),求h的值(精确到米). -
20、宽与长的比是(约为)的矩形叫做黄金矩形.现有一张黄金矩形纸片 , 长 . 如图1,折叠纸片 , 点B落在上的点E处,折痕为 , 连接 , 然后将纸片展开.
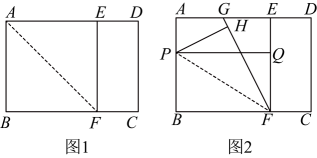 (1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由.
(1)、求的长;(2)、求证:四边形是黄金矩形;(3)、如图2,点G为的中点,连接 , 折叠纸片 , 点B落在上的点H处,折痕为 , 过点P作于点Q . 四边形是否为黄金矩形?如果是,请证明:如果不是,请说明理由.