-
1、智能机器人广泛应用于智慧农业.为了降低成本和提高采摘效率,某果园引进一台智能采摘机器人进行某种水果采摘.(1)、若用人工采摘的成本为a元,相比人工采摘,用智能机器人采摘的成本可降低 . 求用智能机器人采换的成本是多少元;(用含a的代数式表示)(2)、若要采摘4000千克该种水果,用这台智能采摘机器人采摘比4个工人同时采摘所需的天数还少1天,已知这台智能采摘机器人采摘的效率是一个工人的5倍,求这台智能采摘机器人每天可采摘该种水果多少千克.
-
2、如图,曲线过点 .
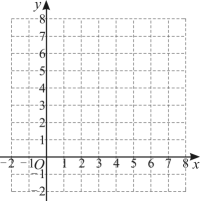 (1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率.
(1)、求t的值;(2)、直线也经过点P , 求l与y轴交点的坐标,并在图中画出直线l;(3)、在(2)的条件下,若在l与两坐标轴围成的三角形内部(不包含边界)随机取一个格点(横、纵坐标都是整数的点),求该格点在曲线G上的概率. -
3、为了弘扬中华优秀传统文化,某校开展主题为“多彩非遗,国韵传扬”的演讲比赛.评委从演讲的内容、能力、效果三个方面为选手打分,各项成绩均按百分制计.进入决赛的前两名选手需要确定名次(不能并列),他们的单项成绩如下表所示:
选手
内容
能力
效果
甲
乙
(1)、分别计算甲、乙两名选手的平均成绩(百分制),能否以此确定两人的名次?(2)、如果评委认为“内容”这一项最重要,内容、能力、效果的成绩按照的比确定,以此计算两名选手的平均成绩(百分制),并确定两人的名次;(3)、如果你是评委,请按你认为各项的“重要程度”设计三项成绩的比,并解释设计的理由. -
4、求代数式的值,其中 .
-
5、如图, , , . 求证: .
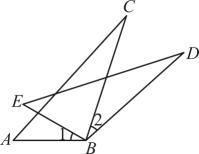
-
6、解不等式组 , 并在数轴上表示解集.
-
7、已知的半径为 , 所在平面内有一动点 , 过点可以引的两条切线 , , 切点分别为 , . 点与圆心的距离为 , 则的取值范围是;若过点作交直线于点(点不与点重合),线段与交于点 . 设 , , 则关于的函数解析式为 .
-
8、若抛物线的顶点在直线上,则m的值为 .
-
9、如图,在中, , 平分 , 已知 , , 则点B到的距离为 .

-
10、要使代数式有意义,则x的取值范围是 .
-
11、如图,在中,点 , 分别在 , 上, , 若 , 则 .
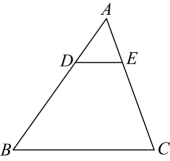
-
12、如图,直线 , 相交于点O . 若 , 则的度数为 .
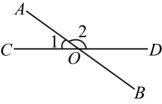
-
13、在平面直角坐标系中,两点 , 在抛物线 , 则下列结论中正确的是( )A、当且时,则 B、当时,则 C、当且时,则 D、当时,则
-
14、如图,的直径 , C为中点,点D在弧上, , 点P是上的一个动点,则周长的最小值是( )
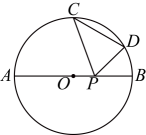 A、 B、 C、 D、
A、 B、 C、 D、 -
15、如图,菱形的面积为10,点E , F , G , H分别为 , , , 的中点,则四边形的面积为( )
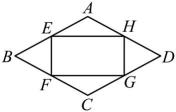 A、 B、5 C、4 D、8
A、 B、5 C、4 D、8 -
16、若 , 反比例函数的图象在( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限
-
17、如图,在平面直角坐标系中,点 , 点 , 若将直线向上平移d个单位长度后与线段有交点,则d的取值范围是( )
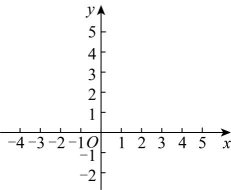 A、 B、 C、 D、
A、 B、 C、 D、 -
18、某地一周的每天最高气温如下表,利用这些数据绘制了下列四个统计图,最适合描述气温变化趋势的是( )
星期
一
二
三
四
五
六
日
最高气温/℃
25
25
28
30
33
30
29
A、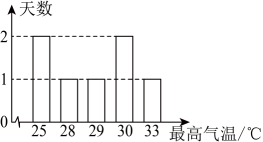 B、
B、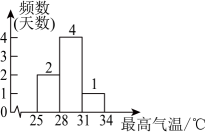 C、
C、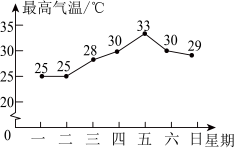 D、
D、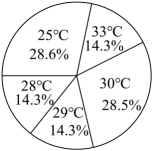
-
19、关于x的方程根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根
-
20、下列运算正确的是( )A、 B、 C、 D、