-
1、在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A'B'C' , 其中△A'B'C'与△ABC的位似比为2;
(2)写出△A'B'C'的各顶点坐标.
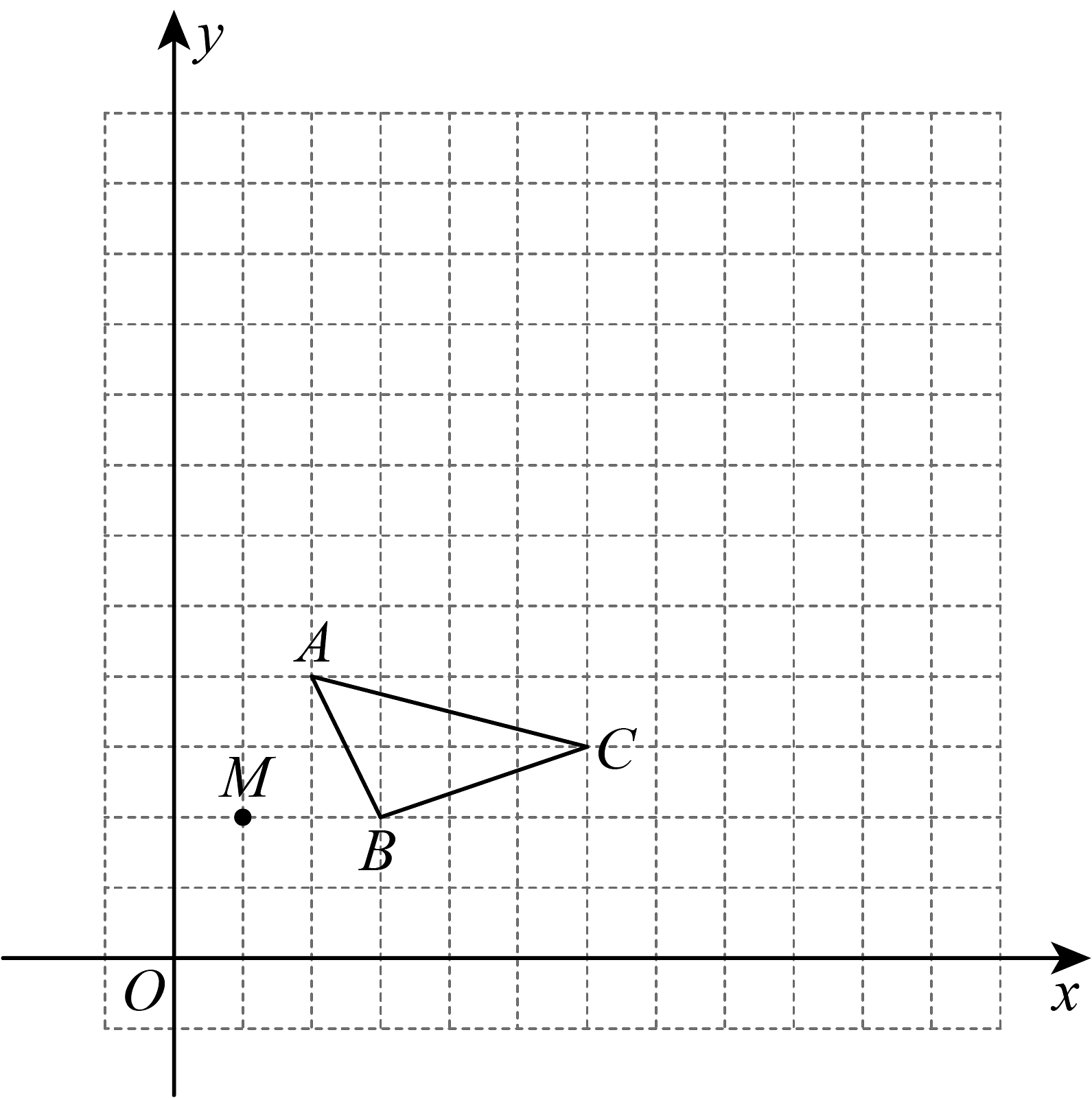
-
2、已知抛物线 .(1)、将化成的形式;(2)、在坐标系中利用描点法画出此抛物线.
x
…
…
y
…
…
 (3)、取何值时,
(3)、取何值时, -
3、已知实数x,y,满足 , 试求的值.
-
4、已知抛物线在坐标系中的位置如图所示,它与x、y轴的交点分别为A、B,P是其对称轴上的动点,根据图中提供的信息,求的最小值( )
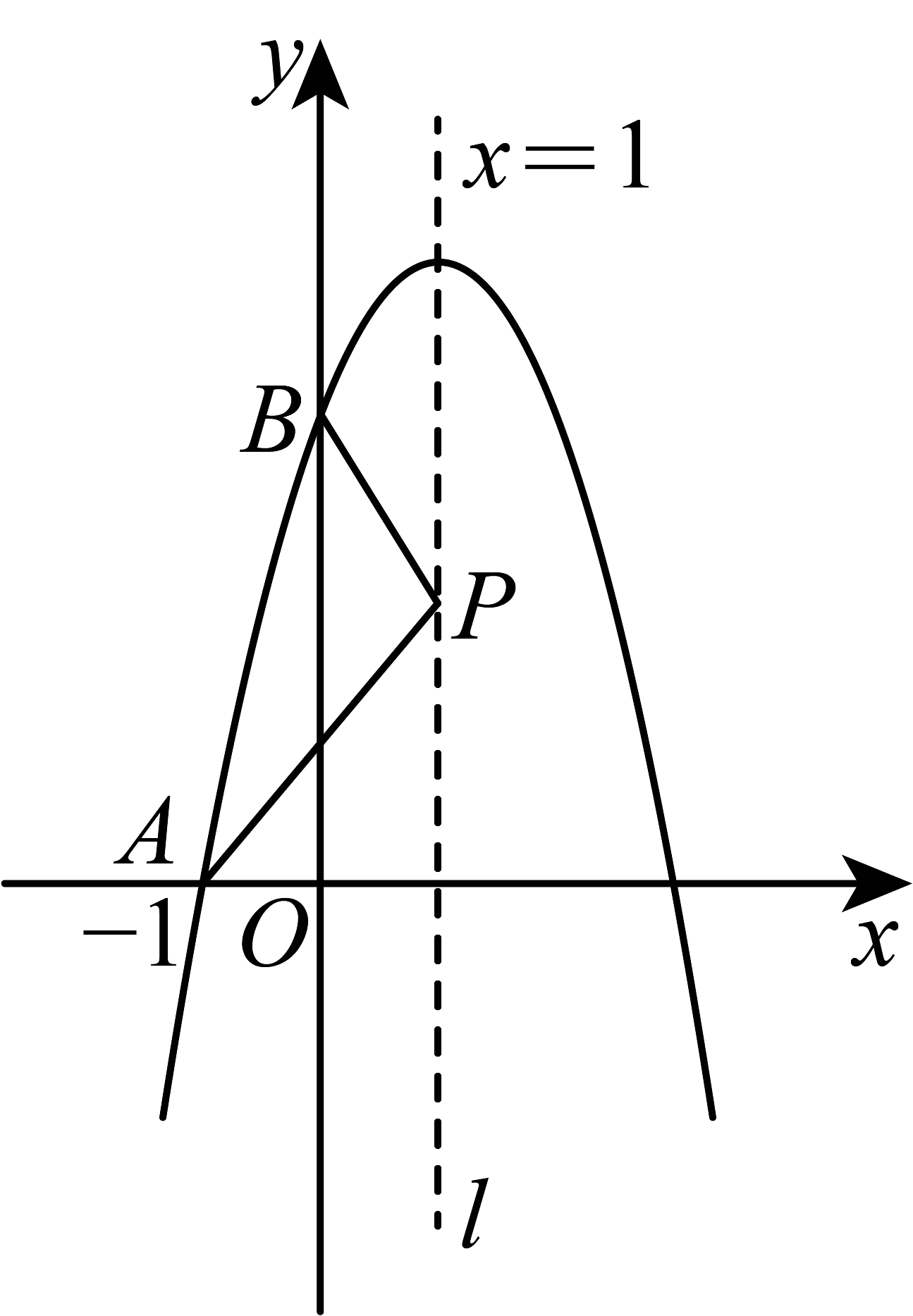 A、 B、 C、5 D、
A、 B、 C、5 D、 -
5、二次函数(a,b,c是常数)的图象如图,则双曲线和直线的位置可能为( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
6、关于反比例函数的说法正确的是( )A、 B、随的增大而减小 C、其图象关于轴对称 D、若点在其图象上,则
-
7、关于二次函数的图象,下列说法错误的是( )A、开口向下 B、对称轴是直线 C、当时,y随x的增大而增大 D、抛物线和x轴交于、
-
8、下列说法正确的是( )A、所有的矩形都是相似形 B、所有的等腰直角三角形都相似 C、对应角相等的两个多边形相似 D、对应边成比例的两个多边形相似
-
9、已知 , 那么下列等式中,不一定正确的是( )A、 B、 C、 D、
-
10、关于二次函数的图象,下列说法正确的是( )A、顶点坐标为 B、顶点坐标为 C、顶点坐标为 D、顶点坐标为
-
11、已知单项式与是同类项,那么的值是( )A、 B、 C、 D、
-
12、综合与实践
折纸是一项有趣的活动,折纸活动也伴随着我们初中数学的学习.在折纸过程中,我们可以研究图形的运动和性质,也可以在思考问题的过程中,初步建立几何直观,现在就让我们带着数学的眼光来折纸吧.定义:将纸片折叠,若折叠后的图形恰能拼合成一个无缝隙、无重叠的长方形,这样的长方形称为完美长方形.
 (1)、操作发现:
(1)、操作发现:如图1,将纸片按所示折叠成完美长方形 , 若的面积为18, , 则此完美长方形的边长_____,面积为_____.
(2)、类比探究:如图2,将纸片按所示折叠成完美长方形 , 若的面积为40, , 求完美长方形的周长.
(3)、拓展延伸:如图3,将纸片按所示折叠成完美长方形 , 若 , , 求此完美长方形的周长与面积.
-
13、如图,()是一张周长为36厘米的长方形纸片,设长方形纸片的长为x厘米,将纸片的四个角各剪下一个边长为2厘米的正方形.
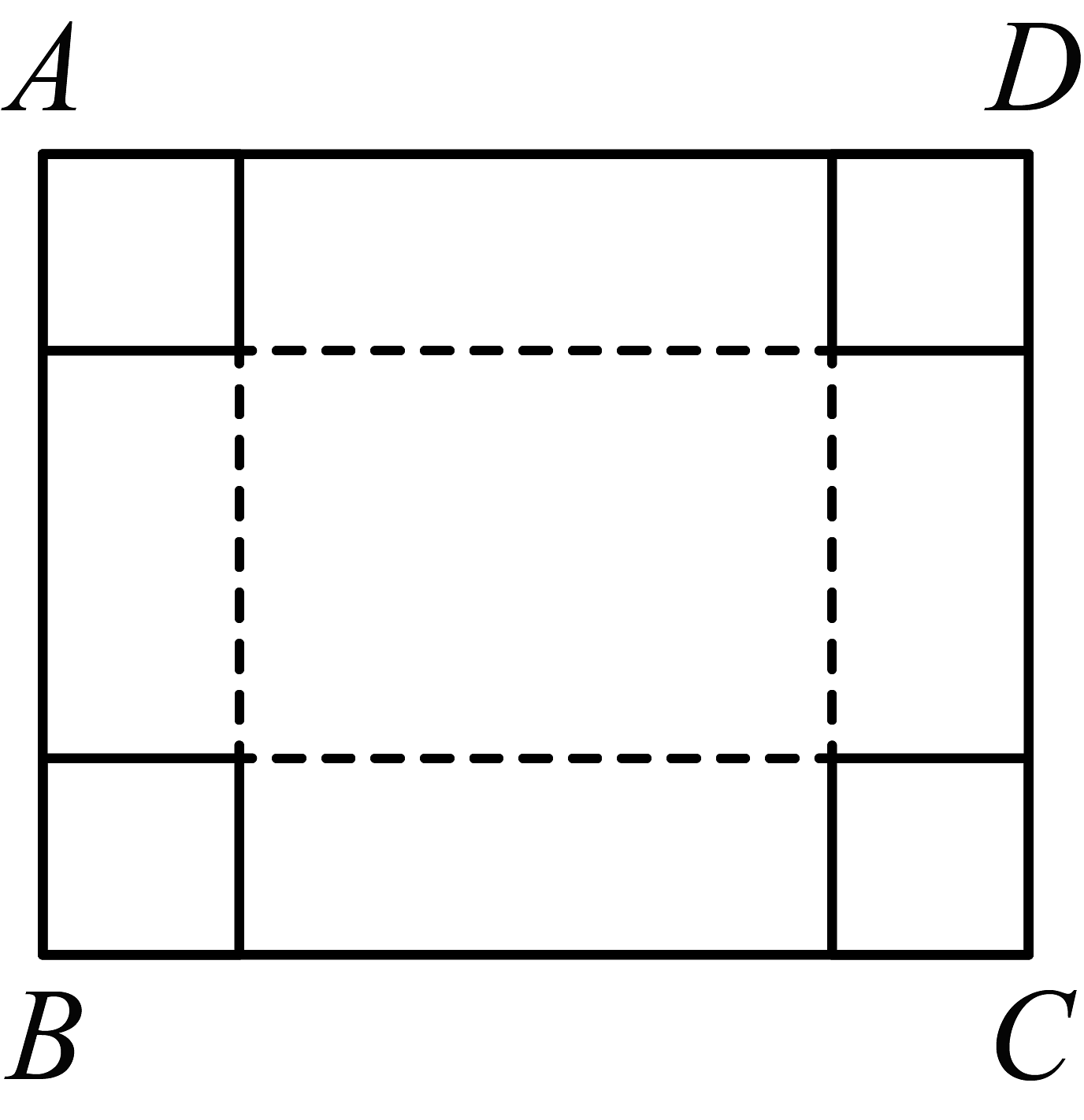 (1)、如果剪去四个角剩下的纸片的面积为 , 请用含有x的式子表示(结果要求化简);(2)、如图,沿虚线将剪去四个角剩下的纸片折成一个无盖的长方体纸盒,如果所得的长方体纸盒的体积是48立方厘米,求的长.
(1)、如果剪去四个角剩下的纸片的面积为 , 请用含有x的式子表示(结果要求化简);(2)、如图,沿虚线将剪去四个角剩下的纸片折成一个无盖的长方体纸盒,如果所得的长方体纸盒的体积是48立方厘米,求的长. -
14、如图,线段 , 与交于点E.
 (1)、求证:;(2)、过点E作 , 交于点F,如果 , , 求的长.
(1)、求证:;(2)、过点E作 , 交于点F,如果 , , 求的长. -
15、中国古代有着辉煌的数学成就,:《周髀算经》,:《九章算术》,:《海岛算经》,:《孙子算经》等是我国古代数学的重要文献.(1)、小聪想从这4部数学名著中随机选择1部阅读,则他选中《九章算术》的概率为___________;(2)、某中学拟从这4部数学名著中选择2部作为“数学文化”校本课程学习内容,求恰好选中:《周髀算经》和:《海岛算经》的概率.(用树状图或列表的方法)
-
16、如图,在平面直角坐标系中,的顶点坐标分别为 .
 (1)、以原点为位似中心,在第一象限内画出的位似图形 , 使它与的相似比为 .(2)、在(1)的条件下,若为内部的一点,则点在内部的对应点的坐标为 .
(1)、以原点为位似中心,在第一象限内画出的位似图形 , 使它与的相似比为 .(2)、在(1)的条件下,若为内部的一点,则点在内部的对应点的坐标为 . -
17、如图,在中,C、E 和 D、F 分别是、的三等分点,且 , 则 .

-
18、已知点是线段的黄金分割点,若 , 则线段的长为 .
-
19、已知是方程的一个根,则的值是( )A、 B、6 C、4 D、
-
20、任意抛掷一枚均匀的骰子两次,记两次朝上的点数的和为m,则下列m的值中,概率最大的是( )A、6 B、7 C、8 D、9