相关试卷

1、已知二次函数 $y = - \frac{3}{4} x^{2} + 3 x - 2,$ 当0≤x≤m时，函数的最小值为-2，最大值为1，则m的取值范围是（）

A、-1≤m≤0 B、 $2 \leq m < \frac{7}{2}$ C、2≤m≤4 D、m≥2

查看解析
2、已知抛物线 $y = x^{2} + (2 a - 1) x - 3,$ 当--1≤x≤3时，函数的最大值为1，则a的值为（）

A、 $- \frac{1}{2}$ B、 $- \frac{1}{3}$ C、 $- \frac{1}{2}$ 或 $- \frac{1}{3}$ D、-1或 $- \frac{1}{3}$

查看解析
3、已知二次函数 $y = a x^{2} + 4 a x + 3 a (a⟩ 0 ）,$ 若-3≤x≤1，则函数 y的最大值为（用含a的代数式表示）.

查看解析
4、已知二次函数 $y = 2 x^{2} - 4 x - 1,$ 在0≤x≤a时，y的最大值为15，则a的值为（）

A、1 B、2 C、3 D、4

查看解析
5、已知二次函数： $y = {(x - 2)}^{2} + 3,$ ，则当1≤x≤4时，该函数（）

A、有最大值7，有最小值4 B、只有最大值7，无最小值 C、只有最小值3，无最大值 D、有最小值3，有最大值7

查看解析
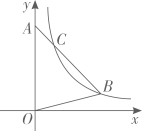
6、如图，在△OAB 中，边 OA 在 y 轴上.反比例函数 $y = \frac{k}{x} (x⟩ 0 ）$ 的图象恰好经过点 B，与边AB交于点 C.若BC=3AC，S_△OAB=10，则k的值为

查看解析
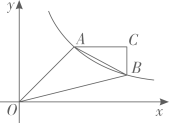
7、如图，在平面直角坐标系xOy中，函数 $y = \frac{k}{x}$ （k为大于0的常数，x>0）图象上的两点 A（x₁ ， y₁），B（x₂ ， y₂），满足x₂=2x₁ ， △ABC 的边 AC∥x 轴，边 BC∥y轴.若△OAB 的面积为 6，则△ABC 的面积是.

查看解析
8、如图， P 是函数 $y = \frac{k_{1}}{x}$ （k₁>0，x>0）的图象上一点，过点 P 分别作x轴和 y轴的垂线，垂足分别为 A，B，交函数 $y = \frac{k_{2}}{x} (k_{2} ＞ 0 ， x ＞ 0)$ 的图象于点 C，D，连结OC，OD，CD，AB，其中 $k_{1} > k_{2} .$ 有下列结论：①CD∥AB；②S_△OCD = $\frac{k_{1} - k_{2}}{2}$ ；③S_△DCP = $\frac{{(k_{1} - k_{2})}^{2}}{2 k_{1}},$ 其中正确的是（）

A、①② B、①③ C、②③ D、①

查看解析
9、如图，D为矩形ABCO的边AB 的中点，反比例函数 $y = \frac{k}{x} (k⟩ 0 ）$ 的图象经过点 D，交 BC边于点 E.若△BDE 的面积为2，则k的值为（）

A、6 B、7 C、8 D、9

查看解析
10、反比例函数 $y = \frac{k}{x}$ 和 $y = \frac{2}{x}$ 在第一象限内的图象如图所示，点P 在 $y = \frac{k}{x}$ 的图象上，过点 P 作 PA⊥x轴于点 A，交 $y = \frac{2}{x}$ 的图象于点 C，PB⊥y轴于点 B，交 $y = \frac{2}{x}$ 的图象于点 D.当点 P 的横坐标逐渐变大时，四边形OCPD的面积（）

A、逐渐变大 B、逐渐变小 C、不变 D、无法确定

查看解析
11、如图，反比例函数 $y = \frac{k}{x} （ k \neq 0, x < 0 ）$ 的图象经过A，B两点，分别过点A，B作x轴的垂线 AC，BD，垂足分别为 C，D，连结AO，连结BO交AC 于点 E.若△AEO 的面积为3，则四边形 BDCE 的面积是（）

A、2 B、 $\frac{3}{2}$ C、3 D、1

查看解析
12、如图，点 A 在反比例函数. $y = \frac{4}{x} (x⟩ 0 ）$ 的图象上，点B 在反比例函数 $y = \frac{k}{x} （ x < 0 ）$ 的图象上，AB∥x轴，点C在x 轴上，△ABC的面积为3，则k的值为（）

A、1 B、-1 C、2 D、-2

查看解析
13、如图，P 为反比例函数 $y = \frac{k}{x} (k⟩ 0 ）$ 图象上一点，作PA⊥x轴于点A，Q为该反比例函数图象上不同于点 P 的另一个点，作QC⊥y轴于点C，延长CQ，AP 交于点E，连结OP，OQ.

(1)、求证： $\frac{E Q}{C Q} = \frac{E P}{A P};$

(2)、连结PQ，AC，则 PQ与AC 的位置关系是.

查看解析
14、如图，反比例函数 $y = \frac{m}{x} (m⟩ 0, x > 0 ）$ 与一次函数y=kx+b的图象交于A（x_A ， y_A），B（x_B ， y_B）两点，求△AOB 的面积（用点A，B的坐标表示）.

查看解析
15、已知反比例函数 $y = \frac{k}{x} (k⟩ 0 ）,$ 请用含k的代数式表示下列阴影部分的面积：

(1)、
S_阴影 =

(2)、
S_阴影=

(3)、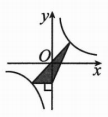
S_阴影=

(4)、
S_阴影═

(5)、
S_阴影═

(6)、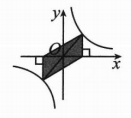
S_阴影═

查看解析
16、某学校为美化学校环境，打造绿色校园，决定用篱笆围成一个一面靠墙（墙足够长）的矩形花园，用一道篱笆把花园分为A，B两块（如图所示），花园里种满牡丹和芍药.学校已定购篱笆120米.

(1)、设计一个使花园面积最大的方案，并求出其最大面积；

(2)、在花园面积最大的条件下，A，B两块内分别种植牡丹和芍药，每平方米种植2株.已知牡丹每株售价25 元，芍药每株售价15元，学校计划购买费用不超过5万元，求最多可以购买多少株牡丹.

查看解析
17、某小区在一块矩形ABCD的空地上划一块四边形 MNPQ进行绿化.如图，已知矩形的边 BC=200 m，边AB=160m，四边形MNPQ的顶点在矩形的边上，且 DQ=BN=2AM= 2CP=2x m.设四边形MNPQ的面积为 S m².

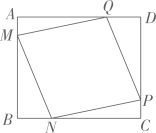(1)、S关于x 的函数关系式为，自变量x的取值范围为；

(2)、若为了小区老人有足够的运动区域，要求AQ不少于 80 m，求此时S的最小值及相应的x的值；

(3)、若每平方米绿化费用需5元，求绿化的最低费用为多少万元.

查看解析
18、某市农副产品销售公司的某农副产品的年产量不超过100万件，该产品的生产费用y（万元）与年产量x（万件）之间的函数图象是顶点为原点的抛物线的一部分（如图①所示）；该产品的售价z（元/件）与年产量x（万件）之间的函数图象是如图②所示的一条线段.生产出的产品都能在当年销售完，达到产销平衡，所获毛利润为ω 万元.（毛利润=销售额一生产费用）

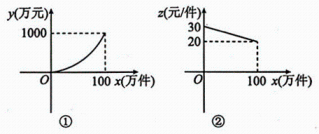(1)、求出 y 与x 以及z与x 之间的函数关系式；

(2)、求ω与x之间的函数关系式；

(3)、由于受资金的影响，今年投入生产的费用不会超过490万元，求今年可获得的最大毛利润.

查看解析
19、综合与实践
问题情境
小莹妈妈的花卉超市以 15 元/盆的价格新购进了某种盆栽花卉，为了确定售价，小莹帮妈妈调查了附近 A，B，C，D，E五家花卉店近期该种盆栽花卉的售价与日销售量情况，记录如下表：
数据整理

(1)、请将以上调查数据按照一定顺序重新整理，填写在下表中：
售价（元/盆）
日销售量（盆）

(2)、模型建立
分析数据的变化规律，找出日销售量与售价间的关系.

(3)、拓广应用
根据以上信息，小莹妈妈在销售该种花卉中，
①要想每天获得400元的利润，应如何定价?
②售价定为多少时，每天能够获得最大利润?

查看解析
20、任务驱动：2024 年世界泳联跳水世界杯第三站暨超级总决赛于 4 月 19 日至 21 日在中国陕西省西安市成功举办，中国国家跳水队以8金1银总奖牌 9枚完美收官，进一步激发各地跳水运动员训练的热情.数学小组对跳水运动员跳水训练进行实践调查.
研究步骤：如图，某跳水运动员在 10 米跳台上进行跳水训练，水面与 y 轴交于点E（0，-10），运动员（将运动员看成一点）在空中运动的路线是经过原点O的抛物线，在跳某个规定动作时，运动员在空中最高处点 A的坐标为 $(\frac{3}{4}, \frac{9}{16}) .$ 正常情况下，运动员在距水面高度5米之前，必须完成规定的翻腾、打开动作，并调整好入水姿势，否则就会失误，运动员入水后，运动路线为另一条抛物线.
问题解决：请根据上述研究步骤与相关数据，完成下列任务.

(1)、求运动员在空中运动时对应抛物线的表达式及入水处点 B的坐标；

(2)、若运动员在空中调整好入水姿势时，恰好与y轴的水平距离为3米，则该运动员此次跳水会不会失误?说明理由；

(3)、在该运动员入水处点 B的正前方有M，N两点，且EM=6，EN=8，该运动员入水后运动路线对应抛物线的表达式为 $y = {(x - h)}^{2} +$ k.若该运动员出水处点 D 在点M，N之间（包括M，N两点），请求出k的取值范围.

查看解析

上一页 202 203 204 205 206 下一页跳转

售价（元/盆）
日销售量（盆）