-
1、如图,在4×5的网格中,每个小正方形的边长均为1.若△ABC的顶点都在格点上,则 sin C 的值为.

-
2、 如图是一架人字梯,已知AB=AC=2米,AC与地面 BC的夹角为α,则两梯脚之间的距离 BC为( )
 A、4cosα米 B、4sinα米 C、4tanα米 D、米
A、4cosα米 B、4sinα米 C、4tanα米 D、米 -
3、学校开放日即将来临,负责布置的林老师打算从学校图书馆的顶楼拉出一条彩旗绳AB到地面,如图所示.已知彩旗绳与地面形成25°角(即∠BAC=25°),彩旗绳固定在地面的位置与图书馆相距32 米(即AC=32米),则彩旗绳AB 的长度为( )
 A、32sin 25°米 B、32cos 25°米 C、米 D、米
A、32sin 25°米 B、32cos 25°米 C、米 D、米 -
4、 如图,某游乐场一山顶滑梯的坡角为α,高为h,则滑梯的长l为( )
 A、hsinα B、htanα C、 D、
A、hsinα B、htanα C、 D、 -
5、
仰角和俯角
仰角:在视线与水平线所成的角中,视线在水平线上方的叫仰角.

俯角:视线在水平线下方的叫俯角
坡比和坡角
坡比:坡面的铅直高度 h 和水平宽度l的比叫做坡面的坡比,记作i=
坡角:坡面与水平面的夹角叫做坡角,记作α,i=tanα
坡比越大,坡角α越大,坡面
方向角
指北或指南方向线与目标方向线所成的小于90°的角叫做方向角

-
6、 如图,已知△ABC.
 (1)、如图①,在△ABC中,∠C=90°,BC=6, , 则AB= , AC= , sin B= , tan B=;(2)、如图②,在△ABC中,∠B=45°,∠C=60°,AC=8,则AB=;(3)、如图③,在△ABC中,∠B=30°,BC=10,∠ACB=135°,则 BC边上的高线长为.
(1)、如图①,在△ABC中,∠C=90°,BC=6, , 则AB= , AC= , sin B= , tan B=;(2)、如图②,在△ABC中,∠B=45°,∠C=60°,AC=8,则AB=;(3)、如图③,在△ABC中,∠B=30°,BC=10,∠ACB=135°,则 BC边上的高线长为. -
7、
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b
三边关系
a2+b2=
两锐角关系
∠A+∠B=°
边与角关系
sin A = cos B= , cos A=sin B= , tan A = , tan B=
-
8、 在△ABC中,若锐角∠A,∠B 满足| sin A— 则∠C=.
-
9、
α
sinα
cosα
tanα
30°
45°
60°
-
10、如图,在Rt△ABC中,∠C=90°,若 则 sin A 的值为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
11、
在Rt△ABC中,∠C=90°,AB=c,BC=a,AC=b
正弦
余弦
正切
∠A 的正弦、余弦、正切统称为∠A 的锐角三角函数.由定义可知,∠A为锐角时,0< sin A<1,0< cos A<1
-
12、如图,△ABC 是⊙O的内接三角形,AB 是⊙O的直径, 2 , 点 F 在 AB 上,连结 CF 并延长,交⊙O于点 D,连结 BD,作 BE⊥CD,垂足为点 E.
 (1)、求证:△DBE∽△ABC;(2)、若AF=2,求 ED的长.
(1)、求证:△DBE∽△ABC;(2)、若AF=2,求 ED的长. -
13、四个边长均为1的正方形如图摆放,其中三个顶点位于坐标轴上,一个顶点在反比例函数 0)的图象上,则k的值为 ( )
 A、5 B、6 C、7 D、8
A、5 B、6 C、7 D、8 -
14、李阿姨要装修自己带阁楼的新居(如图为新居剖面图),在建造客厅到阁楼的楼梯AC时,为避免上楼时墙角 F 碰头,设计墙角F到楼梯的竖直距离 FG 为1.75 m.已知客厅高AB=2.8 m,楼梯洞口宽 AF=2m ,阁楼阳台宽 EF=3m.如果要使墙角 F 到楼梯的竖直距离 FG 为 1.75 m,那么楼梯底端 C到墙角D 的距离CD 是多少米?

-
15、 如图,矩形 OABC 各顶点的坐标分别为O(0,0),A(3,0),B(3,2),C(0,2),以原点O为位似中心,将这个矩形按相似比 缩小,则顶点 B在第一象限内的对应点的坐标是.

-
16、如图,在平面直角坐标系中,△ABC 与△A'B'C'是位似图形,位似中心为点O.若点A(-3,1)的对应点为 A'(-6,2),则点B(-2,4)的对应点 B'的坐标为( )
 A、(-4,8) B、(8,-4) C、(-8,4) D、(4,-8)
A、(-4,8) B、(8,-4) C、(-8,4) D、(4,-8) -
17、如图,O为四边形ABCD 内一点,连结OA,OB,OC,OD.若 则四边形A'B'C'D'的面积与四边形 ABCD 的面积之比为( )
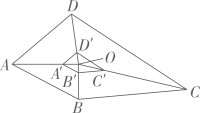 A、1:2 B、1:4 C、1:8 D、1:16
A、1:2 B、1:4 C、1:8 D、1:16 -
18、手工制作课上,小红利用一些花布的边角料,剪裁后装饰手工画.下面四个图案(图)是她剪裁出的空心不等边三角形、等边三角形、正方形和矩形花边,其中每个图案花边的宽度都相同,那么图案中花边的内外边缘所围成的几何图形不一定相似的是( )A、
 B、
B、 C、
C、 D、
D、
-
19、 如图,小明在 A时测得某树的影长为8 m,B 时又测得该树的影长为2m,若两次日照的光线互相垂直,则树的高度为( )
 A、2m B、4m C、6m D、8m
A、2m B、4m C、6m D、8m -
20、如图
 (1)、【基础巩固】如图①,在△ABC 中,D 是AB 上.的一点,且∠ACD = ∠B,求证:. AB·AD;(2)、【尝试应用】
(1)、【基础巩固】如图①,在△ABC 中,D 是AB 上.的一点,且∠ACD = ∠B,求证:. AB·AD;(2)、【尝试应用】如图②,在(1)的条件下,过点 D 作 DE∥AC,交 BC于点E.若AD: DB=1:3,BC=8,求 CD的长;
(3)、【拓展提高】如图③,在▱ABCD中,E是CD 的中点,连结 BE,AE 交 BD 于点 F,且∠DFA=∠EBA.若 求 tan C 的值.