-
1、
定义
有一组的平行四边形叫做菱形
性质
菱形的四条边都
菱形的对角线互相平分，并且每条对角线平分
菱形是轴对称图形，所在的直线是它的对称轴
菱形是中心对称图形，它的对称中心是
判定
定义法
四条边相等的四边形是菱形
对角线互相垂直的平行四边形是菱形
结论
菱形的面积=底×高
菱形的面积等于乘积的一半
菱形的两条对角线将其分成四个直角三角形，且四个直角三角形的面积相等
-
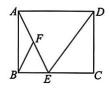
2、 如图，在矩形ABCD 中，点E在边 BC 上，F 是 AE 的中点，AB=8，AD=DE=10，则 BF 的长为.
-
3、 如图，在矩形ABCD中，对角线AC，BD 相交于点O，∠ABD=60°，AB=2，则AC的长为（ ）
A、6 B、5 C、4 D、3 -
4、已知四边形 ABCD 是平行四边形，下列条件中，不能判定▱ABCD为矩形的是（ ）A、∠A=90° B、∠B=∠C C、AC=BD D、AC⊥BD
-
5、
定义
有一个角是的平行四边形叫做矩形
性质
矩形的四个角都是
矩形的对角线互相平分并且
矩形是轴对称图形，它（非正方形）有条对称轴
矩形是中心对称图形，它的对称中心是
判定
定义法
有个角是直角的四边形是矩形
对角线的平行四边形是矩形
结论
矩形的面积等于两邻边的积
矩形的两条对角线把矩形分成四个三角形，且四个三角形的面积相等
-
6、如图，在□ABCD 中，AC，BD 相交于点 O，AC=2，BD=2过点A 作AE⊥BC于点E，记BE的长为x，BC的长为y.当x，y的值发生变化时，下列代数式的值不变的是 （ ）
A、x+y B、x-y C、xy D、 -
7、如图1，▱ABCD 中，AD>AB，∠ABC为锐角.要在对角线 BD上找点N，M，使四边形ANCM为平行四边形，现有图2中的甲、乙、丙三种方案，则正确的方案 （ ）
图1
图2A、甲、乙、丙都是 B、只有甲、乙才是 C、只有甲、丙才是 D、只有乙、丙才是 -
8、如图，E 为□ABCD的对角线AC上一点，AC=5，CE=1，连结 DE并延长至点 F，使得 EF=DE，连结 BF，则BF的长为 （ ）
A、 B、3 C、 D、4 -
9、如图，在▱ABCD中， 连结 BE，交 AC 于点 F，AC=5，则CF的长为.
-
10、如图，在▱ABCD中，AB=8，∠ABC=60°，BE 平分∠ABC，交边 AD 于点E，连结CE，若AE=2ED，则CE的长为 （ ）
A、6 B、4 C、4 D、2 -
11、如图，在▱ABCD 中， AB=2，∠ABC的平分线与∠BCD 的平分线交于点E.若点 E 恰好在边 AD 上，则. 的值为.
-
12、如图，在□ABCD 中， ∠ABC 的平分线相交于点 G，且分别交CD于点E，F.若 DF=3，EF=2，AG=kGE，则k=（ ）
A、2 B、3 C、4 D、5 -
13、 下面是嘉嘉作业本上的一道习题及解答过程：
已知：如图，在△ABC中，AB=AC，AE平分△ABC的外角∠CAN，M是AC 的中点，连结BM并延长交AE 于点D，连结CD.
求证：四边形 ABCD 是平行四边形.
证明：∵AB=AC，
∴∠ABC=∠3.
∵∠CAN=∠ABC+∠3，∠CAN=∠1+∠2，∠1=∠2，∴① ▲ .
又∵∠4=∠5，MA=MC，
∴△MAD≌△MCB（② ），
∴MD=MB，∴四边形ABCD 是平行四边形.
若以上解答过程正确，则①，②应分别为（ ）
A、∠1=∠3，AAS B、∠1=∠3，ASA C、∠2=∠3，AAS D、∠2=∠3，ASA -
14、
判定
两组对边
两组对边的四边形是平行四边形
两组对边的四边形是平行四边形
一组对边
一组对边的四边形是平行四边形
两条
对角线
对角线的四边形是平行四边形
-
15、 如图，在▱ABCD 中，AB=3cm，BC=5cm，AB⊥AC，则 BD的长度为 cm.
-
16、 如图，在□ABCD中，AB=5，BC=8，∠ABC的平分线 BE 交边 AD 于点 E，则 DE 的长为.
-
17、 如图， □ABCD 的对角线 AC与 BD相交于点O，则下列结论一定正确的是（ ）
A、AB=BC B、AD=BC C、OA=OB D、AC⊥BD -
18、
定义
两组对边分别平行的四边形叫做平行四边形
性质
（1）边：对边；
（2）角：对角 ， 邻角；
（3）对角线：对角线；
（4）对称性：平行四边形是中心对称图形，对称中心是；
（5）四边形具有不稳定性
-
19、 如图，由六个正九边形可以拼接成一个美丽的梅花形图案，则图中∠ABC的度数为 （ ）
A、60° B、70° C、80° D、90° -
20、 若正多边形的一个外角是60°，则这个正多边形的边数是（ ）A、4 B、5 C、6 D、7