相关试卷

1、阅读下面的材料：
因为 $\frac{1}{1 \times 3} = \frac{1}{2} \times (1 - \frac{1}{3})$ ， $\frac{1}{3 \times 5} = \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5})$ ， $\frac{1}{5 \times 7} = \frac{1}{2} \times (\frac{1}{5} - \frac{1}{7})$ ， $\dots$ ， $\frac{1}{17 \times 19} = \frac{1}{2} \times (\frac{1}{17} - \frac{1}{19})$ ，
所以 $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{17 \times 19} = \frac{1}{2} \times (1 - \frac{1}{3}) + \frac{1}{2} \times (\frac{1}{3} - \frac{1}{5}) + \frac{1}{2} \times (\frac{1}{5} - \frac{1}{7}) + \dots + \frac{1}{2} \times (\frac{1}{17} - \frac{1}{19}) = \frac{1}{2} \times (1 - \frac{1}{3} + \frac{1}{3} - \frac{1}{5} + \frac{1}{5} - \frac{1}{7} + \dots + \frac{1}{17} - \frac{1}{19}) = \frac{1}{2} \times (1 - \frac{1}{19}) = \frac{9}{19}$ .
根据上面的方法，解方程： $\frac{1}{x (x + 3)} + \frac{1}{(x + 3) (x + 6)} + \frac{1}{(x + 6) (x + 9)} = \frac{3}{2 x + 18}$ .

查看解析
2、博物院是一座城市重要的公共文化窗口.十一假期，某学习小组计划到河北省博物院参观学习，该小组原计划花360元请讲解人员进行解说，后来临时增加3名同学，总讲解费增加了60元，但人均费用变为原来的 $\frac{14}{15}$ .

(1)、求该学习小组的实际参观人数；

(2)、参观结束后，同学们到文创店购买“长信宫灯”和“错金铜博山炉”纪念卡，已知每套“长信宫灯”和“错金铜博山炉”的单价分别为10元和8元，若该小组每名参观的同学都购买了一套纪念卡，且该小组购买纪念卡的总费用不超过140元，求最多购买了多少套“长信宫灯”纪念卡.

查看解析
3、嘉嘉和琪琪在争论这样一个问题：
嘉嘉说：“分式 $\frac{x}{x - 1}$ 比 $\frac{3}{(x - 1) (x + 2)}$ 多1时， $x$ 的值是1.”
琪琪说：“分式 $\frac{x}{x - 1}$ 比 $\frac{3}{(x - 1) (x + 2)}$ 多1的情况根本不存在.”
你同意谁的观点呢？请说明理由.

查看解析
4、先化简： $(1 - \frac{1}{x - 1}) \div \frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，然后从 $0 \leq x \leq 2$ 的范围内选取一个合适的整数作为 $x$ 的值代入求值.

查看解析
5、计算：

(1)、 $\frac{3}{x - 3} - \frac{x}{x - 3}$ ；

(2)、 $(\frac{1}{x^{2} - 4} + \frac{4}{x + 2}) \div \frac{1}{x - 2}$ .

查看解析
6、有依次排列的不为零的代数式 $a_{1} = x + 1$ ， $a_{2} = x^{2} - 1$ ，且 $a_{3} = \frac{a_{2}}{a_{1}}$ ， $a_{4} = \frac{a_{3}}{a_{2}}$ ， $a_{5} = \frac{a_{4}}{a_{3}}$ ， $\dots$ ，依次类推，若 $a_{n} = \frac{1}{x - 1}$ ，请用含 $k (k$ 为正整数 $)$ 的式子表示 $n :$ .

查看解析
7、2024年12月4日，“春节——中国人庆祝传统新年的社会实践”成功列入联合国教科文组织人类非物质文化遗产代表作名录.为了迎接2025年春节的到来，盼盼家里开始准备年货，购买了 $A$ ， $B$ 两种糖果，其中 $A$ 类糖果的价格比 $B$ 类糖果的价格每千克多2元，花100元购买 $A$ 类糖果的质量与花90元购买 $B$ 类糖果的质量相同，则 $A$ 类糖果的价格为元/千克.

查看解析
8、若关于 $x$ 的不等式组 $\{\begin{array}{l} 3 x + 5 \leq 2 x + 6, \\ x + 1 > a \end{array}$ 无解，且关于 $y$ 的分式方程 $\frac{5 - a y}{2 - y} - 1 = \frac{3}{y - 2}$ 的解为整数，则满足条件的整数 $a$ 的值为（）

A、2或3 B、2或7 C、3 或4或7 D、2 或3或7

查看解析
9、下列说法：①解分式方程一定会产生增根；②方程 $\frac{x - 2}{x^{2} - 4 x + 4} = 0$ 的根为 $x = 2$ ；③方程 $\frac{1}{2 x} = \frac{1}{2 x - 4}$ 的最简公分母为 $2 x (2 x - 4)$ .其中正确的个数是（）

A、0 B、1 C、2 D、3

查看解析
10、若沿河两地相距 $m k m$ ，船在静水中的速度为 $b k m / h$ ，水流的速度为 $c k m / h$ ，则船在两地之间往返一次所需的时间是（）

A、 $\frac{2 m}{b + c} h$ B、 $(\frac{m}{b + c} + \frac{m}{b - c}) h$ C、 $\frac{2 m}{b - c} h$ D、 $(\frac{m}{b} + \frac{m}{c}) h$

查看解析
11、化简 $\frac{x^{2}}{y - x} - \frac{x y}{y - x} =$ （）

A、 $- x$ B、 $y - x$ C、 $x - y$ D、 $- x - y$

查看解析
12、下列各式中，不论 $x$ 取何值，分式都有意义的是（）

A、 $\frac{1}{2 x^{2} + 1}$ B、 $\frac{1}{2 x + 1}$ C、 $\frac{1}{3 x - 1}$ D、 $\frac{1}{2 x^{2}}$

查看解析
13、在式子 $\frac{1}{a}$ ， $\frac{2 x y}{π}$ ， $\frac{3 a^{2} b^{3} c}{4}$ ， $\frac{5}{6 + x}$ ， $\frac{x}{7} + \frac{y}{8}$ ， $\frac{x y + 10}{x + y}$ ， $\frac{x^{2}}{x}$ 中，分式的个数是（）

A、2 B、3 C、4 D、5

查看解析
14、如图1，AB=7 cm，AC=5 cm，AC⊥AB，BD⊥AB，垂足分别为A，B.点P在线段AB上以2 cm/s的速度由点A向点B运动，同时，点Q在射线BD上运动.它们运动的时间为t s，当点P运动结束时，点Q运动随之结束.

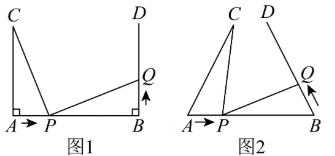(1)、若点Q的运动速度与点P的运动速度相同，当t=1时，△ACP与△BPQ是否全等?并判断此时线段PC和线段PQ的位置关系，请分别说明理由.

(2)、如图2，若“AC⊥AB，BD⊥AB”改为“∠CAB=∠DBA=60°”，点Q的运动速度为x cm/s，其他条件不变，当点P，Q运动到某处时，有△ACP与△BPQ全等，求出相应的x，t的值.

查看解析
15、命题：全等三角形的对应边上的高相等.

(1)、先把这个命题写成“如果……，那么……”的形式，再写出这个命题的逆命题.

(2)、判断原命题的真假，如果是假命题，请举出一个反例；如果是真命题，请写出证明过程.

查看解析
16、如图，∠A=∠B=50°，P为AB的中点，过点P作直线分别交射线AC，BD于点M，N(分别不与点A，B重合)，设∠BPN=α.

(1)、求证：PM=PN.

(2)、当△APM为直角三角形时，求α的度数.

查看解析
17、如图，小明同学拿着老师的等腰直角三角尺，摆放在两摞长方体教具之间，∠ACB=90°，AC=CB，每个小长方体教具高度均为4 cm.

(1)、求证：△ACD≌△CBE.

(2)、求DE的长.

查看解析
18、如图所示，已知线段a及∠α，求作△ABC，使AB=a，AC=2a，∠A=2∠α，写出作法，保留作图痕迹.

查看解析
19、如图，在△ABC中，AD是BC边上的中线，E是AB边上一点，过点C作CF∥AB交ED的延长线于点F.如果AB=10，AE=3，求线段CF的长度.

查看解析
20、如图，AB=AD，∠BAC=∠DAC=25°，∠D=80°.求∠BCA的度数.

查看解析

上一页 15 16 17 18 19 下一页跳转