相关试卷

1、如图，在平面直角坐标系中，第二象限有一点A ，将点A水平向右平移3个单位长度得到点 $A^{'}$ ，过点 $A^{'}$ 分别向x轴、y轴作垂线，垂足分别为B ， C ．若 $A^{'} B = 5, A^{'} C = 2$ ，则点A的坐标为（）

A、 $(- 1, 5)$ B、 $(- 3, 5)$ C、 $(- 1, 2)$ D、 $(2, 5)$

查看解析
2、将点 $P (2, - 5)$ 向右平移3个单位，再向上平移2个单位后的坐标是（）

A、 $(- 1, - 3)$ B、 $(- 1, - 7)$ C、 $(5, - 7)$ D、 $(5, - 3)$

查看解析
3、如图，直角坐标平面 $x O y$ 内，动点 $P$ 按图中箭头所示方向依次运动，第1次从点 $(- 1, 0)$ 运动到点 $(0, 1)$ ，第2次运动到点 $(1, 0)$ ，第3次运动到点 $(2, - 2)$ ．．．按这样的运动规律，动点 $P$ 第2023次运动到点（）

A、 $(2021, - 2)$ B、 $(2021, 1)$ C、 $(2022, 1)$ D、 $(2022, - 2)$

查看解析
4、已知点 $(b, k)$ 在第四象限，则一次函数 $y = k x + b$ 的图象大致是（）

A、 B、 C、 D、

查看解析
5、已知点 $M (x, y)$ 的坐标满足 $x^{2} + | y - 2 | = 0$ ，则点 $M$ 在（）

A、纵轴上 B、横轴上 C、纵轴或横轴上 D、原点处

查看解析
6、若点 $P (a - 3, 1 - a)$ 在第四象限，则a的取值范围是（）

A、 $1 < a < 3$ B、 $a < 1$ C、 $a > 3$ D、无解

查看解析
7、已知二次函数 $y = - x^{2} + 6 x - 5 .$

(1)、求该二次函数图象的顶点坐标.

(2)、当1≤x≤4时，函数的最大值和最小值分别为多少?

(3)、当t≤x≤t+3时，设函数的最大值为m，最小值为n.若m-n=3，求t的值.

查看解析
8、已知抛物线 $y = x^{2} - 2 b x + c .$

(1)、若抛物线的顶点坐标为(2，-3)，求b，c的值.

(2)、若b+c=0，则是否存在实数x，使得对应的y的值为1?请说明理由.

(3)、分类讨论思想若c=b+2，且抛物线在-2≤x≤2上的最小值是-3，求b 的值.

查看解析
9、已知点A(-7，y₁)，B(3，y₂)均在抛物线 $y = a x^{2} + b x + c (a \neq$ 0)上，C(x₀ ， y₀)是该抛物线的顶点，若 $y_{1} >$ $y_{2} \geq y_{0} ，$ ，则x₀的取值范围是.

查看解析
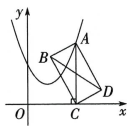
10、如图，点 A 在抛物线 $y = x^{2} - 2 x +$ 2上运动，过点 A 作AC⊥x 轴于点 C，以AC 为对角线作矩形 ABCD，连结 BD，则 BD 长的最小值为

查看解析
11、定义： $m i n {a ， b} = {\begin{matrix} a (a \leq b) ， \\ b (a > b) . \end{matrix}$ 若函数 $y = m i n \{x + 1, - x^{2} + 2 x + 3\}$ ，则该函数的最大值为( )

A、0 B、2 C、3 D、4

查看解析
12、已知二次函数 $y = a x^{2} - 2 a x + 3 (a⟩ 0) ，$ 当0≤x≤m时，3-a≤y≤3，则则 m 的取值范围是( )

A、0≤m≤1 B、0≤m≤2 C、1≤m≤2 D、m≥2

查看解析
13、已知 P₁(x₁ ， y₁)，P₂(x₂ ， y₂)是抛物线 $y = a x^{2} + 4 a x +$ 3(a是常数，且a≠0)上的点，现有下列结论：①该抛物线的对称轴是直线x=-2；② 点(0，3)在抛物线上；③若 $x_{1} > x_{2} >$ -2，则y₁>y₂；④若 $y_{1} = y_{2} ，$ 则 $x_{1} + x_{2} =$ -2.其中，正确的有( )

A、1个 B、2个 C、3个 D、4个

查看解析
14、有一个抛物线形的蔬菜大棚，将其截面放在如图所示的平面直角坐标系中，抛物线对应的函数表达式可以用y= $a x^{2} + b x$ 来表示.已知大棚在地面上的宽度OA 为 8 m，距离点 O 2 m处的棚高 BC 为 $\frac{9}{4}$ m.

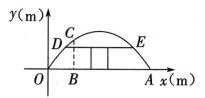(1)、求该抛物线对应的函数表达式.

(2)、求蔬菜大棚离地面的最大高度.

(3)、若借助横梁 DE 建一个门，要求门的高度不低于 1.5m，则横梁 DE 的宽度最大是多少米?

查看解析
15、已知二次函数 $y = 2 x^{2} - 8 x + 11 ，$ 当1≤x≤4时，y的取值范围是.

查看解析
16、已知二次函数 $y = 2 x^{2} - m x + 5 ，$ 当x<-2时，y随x的增大而减小；当x>-2时，y随x 的增大而增大.当x=-1时，y的值是

查看解析
17、已知二次函数 $y = - 2 x^{2} + 12 x - 19 ，$ 当y随x 的增大而增大时，x的取值范围是( )

A、x≥-1 B、x≤-1 C、x≥3 D、x≤3

查看解析
18、已知二次函数y= ${(x - 1)}^{2} + m ，$ 当点(-1，y₁)，(0，y₂)，(4，y₃)在函数图象上时，则y₁ ， y₂ ， y₃的大小关系正确的是( )

A、 $y_{3} < y_{1} < y_{2}$ B、 $y_{2} < y_{1} < y_{3}$ C、 $y_{1} < y_{3} < y_{2}$ D、 $y_{1} < y_{2} < y_{3}$

查看解析
19、关于二次函数 $y = x^{2} + 2 x - 8 ，$ 下列说法中正确的是( )

A、图象的对称轴在 y 轴的右侧 B、图象与 y 轴的交点坐标为(0，8) C、图象与 x 轴的交点坐标为(-2，0)和(4，0) D、y 的最小值为-9

查看解析
20、如图，抛物线 $y = x^{2} + b x + c$ 经过点A(4，—5)，过点 A 分别向 x 轴、y轴作垂线，垂足分别为 B，C，得到矩形ABOC，且抛物线经过点 C.

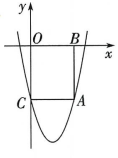(1)、求抛物线对应的函数表达式.

(2)、将抛物线绕直线x=a(0<a<2)翻转，分别交线段 OB，AC 于 D，E 两点.若直线DE 刚好平分矩形ABOC 的面积，求a 的值.

(3)、将抛物线旋转180°，使点 A 的对应点为A₁(m-2，n-4)，其中m≤2.若旋转后的抛物线仍然经过点 A，直接写出旋转后的抛物线的顶点达到最低点时的坐标.

查看解析

上一页 511 512 513 514 515 下一页跳转