-
1、如图,⊙O 的周长为4π,B 是弦CD 上任意一点(不与点 C,D 重合),过点 B 作 OC 的平行线交 OD 于点 E,则 EO+EB 的值为

-
2、在数轴上,点A 所表示的实数为2,点B 所表示的实数为a,⊙A 的半径为 3.若点 B 在⊙A 外,则a 的值可能是( )A、- 1 B、0 C、5 D、6
-
3、在平面直角坐标系中,点P 的坐标为(5,12).若⊙P 的半径为13,则原点与⊙P 的位置关系是( )A、原点在⊙P 内 B、原点在⊙P 上 C、原点在⊙P 外 D、无法确定
-
4、如图,下列说法中,正确的是( )
 A、线段AB,AC,CD 都是⊙O 的弦 B、线段AC 经过圆心O,线段AC 是直径 C、AD=BD D、弦AB 把圆分成两条弧,其中 是劣弧
A、线段AB,AC,CD 都是⊙O 的弦 B、线段AC 经过圆心O,线段AC 是直径 C、AD=BD D、弦AB 把圆分成两条弧,其中 是劣弧 -
5、如图,在平面直角坐标系中,一次函数的图象与轴相交于点 , 与轴相交于点 , 并与直线相交于点 , 其中点的横坐标为3.
 (1)、求点的坐标和的值;(2)、为直线上一动点,当点运动到何位置时,的面积等于?请求出点的坐标.
(1)、求点的坐标和的值;(2)、为直线上一动点,当点运动到何位置时,的面积等于?请求出点的坐标. -
6、在同一平面直角坐标系中,画出正比例函数和的图象.
-
7、随着无人机高科技产业的快速发展,无人机航拍逐渐成为摄影创作的重要形式.某日,学校摄影社团组织汾河冬景无人机航拍活动.如图的平面直角坐标系中,线段 , 分别表示拍摄某镜头时1号、2号无人机飞行高度 , (米)与飞行时间(秒)的函数关系,其中 , 线段与相交于点 , 轴于点 , 点的横坐标为25.
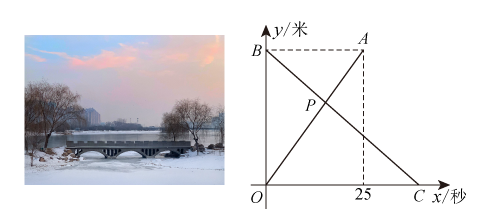 (1)、图中点的坐标为;(2)、求线段对应的函数表达式;(3)、求点的坐标,并写出点坐标表示的实际意义.
(1)、图中点的坐标为;(2)、求线段对应的函数表达式;(3)、求点的坐标,并写出点坐标表示的实际意义. -
8、已知直线经过点且与坐标轴所围成的三角形的面积是 , 求这条直线的表达式.
-
9、已知两地之闻有一条笔直的公路,.甲车从地出发匀速去往地,到达地后立即以原速原路返回地,乙车从地出发匀速去往地,两车同时出发,乙车比甲车晚10分钟到达地.甲车距地的路程为(千米)与甲车行驶的时间(分)之间的函数关系如图所示.
 (1)、在图中画出乙车距地的路程(千米)与(分)之间的函数图象,并求出它所对应的函数关系式(写出自变量的取值范围)(2)、甲、乙两车在行驶过程中相遇了次.(3)、求甲车到达地时,乙车距地的路程.
(1)、在图中画出乙车距地的路程(千米)与(分)之间的函数图象,并求出它所对应的函数关系式(写出自变量的取值范围)(2)、甲、乙两车在行驶过程中相遇了次.(3)、求甲车到达地时,乙车距地的路程. -
10、如下图,点A的坐标为 , 点B的坐标为 , 过点作直线l交于点E , 且三角形的面积为3.
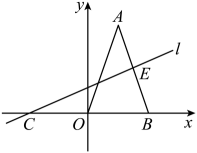 (1)、求直线的函数表达式.(2)、求直线l的函数表达式.
(1)、求直线的函数表达式.(2)、求直线l的函数表达式. -
11、已知直线过点 , 那么关于的二元一次方程的一组解为 .
-
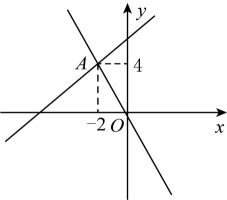
12、如图,一次函数和的图象相交于点 , 则关于、的方程组:的解是 .
-
13、已知函数 , 当函数值时,自变量的取值是( )A、 B、 C、或 D、或
-
14、如图,已知点的坐标为 , 点分别是某函数图象与轴、轴的交点,点是此图象上的一动点,设点的横坐标为的长为 , 且与之间满足关系: , 则以下结论不正确的是( )
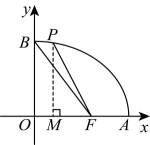 A、 B、 C、 D、
A、 B、 C、 D、 -
15、若点在过原点的一条直线上,则这条直线所对应的函数解析式为( )A、 B、 C、 D、
-
16、已知直线的图象经过点 , , 则关于的方程的解为( )A、 B、 C、 D、
-
17、已知一次函数和一次函数的自变量x与因变量 , 的部分对应数值如表所示,则关于x , y的二元一次方程组的解为( )
x
…
0
1
2
…
…
1
2
4
…
…
1
3
…
A、 B、 C、 D、 -
18、如图,一次函数的图象经过点 , 且与正比例函数的图象交于点 , 则这个一次函数的表达式是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、函数与的图象在同一直角坐标系中,位置关系是( )A、相交 B、互相垂直 C、平行 D、无法确定
-
20、如图,一次函数y=kx+b与正比例函数y=2x的图象交于点A , 则关于x , y的方程组的解为
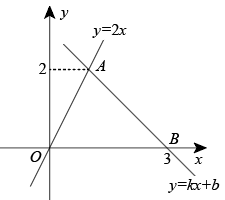 A、 B、 C、 D、
A、 B、 C、 D、