-
1、下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
2、2025年“五一”假期,济南市图书馆推出全民阅读文化市集、集邮展销等活动,累计接待读者96110人次,数据96110用科学记数法表示为( )A、 B、 C、 D、
-
3、如图是由几个大小相同的小立方块搭成的几何体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、
-
4、下列各数中为负数的是( )A、 B、0 C、2 D、
-
5、如图,在正方形中,E,F分别是 , 上的点, , 相交于点P,且 .
 (1)、如图1,求证:;(2)、若 , , 求的长度;(3)、如图2, , , 点F在线段上运动时(点F不与C、D重合),四边形是否能否成为菱形?请说明理由.
(1)、如图1,求证:;(2)、若 , , 求的长度;(3)、如图2, , , 点F在线段上运动时(点F不与C、D重合),四边形是否能否成为菱形?请说明理由. -
6、在平面直角坐标系中,的坐标为 , , , 并求:
 (1)、画出 , 其中 , , ;(2)、将向左平移3个单位后,变为 , 写出的坐标;(3)、求的面积.
(1)、画出 , 其中 , , ;(2)、将向左平移3个单位后,变为 , 写出的坐标;(3)、求的面积. -
7、如图, , , E,F是垂足, . 求证: .

-
8、如图,在平行四边形的边上分别取一个点E,F,使得 , 连接 . 求证:四边形是平行四边形.

-
9、如图,在中, , 于点D, , .
 (1)、求的面积;(2)、求线段的长.
(1)、求的面积;(2)、求线段的长. -
10、已知一个n边形的内角和为 , 求n.
-
11、计算题(1)、;(2)、 .
-
12、如图,在正方形中, , P是线段上的动点,于点E,于点F,则 .

-
13、在中, , , , 则的面积为 .
-
14、在平行四边形中,已知 , , 则它的周长为 .
-
15、已知,在矩形中, , 则对角线 .
-
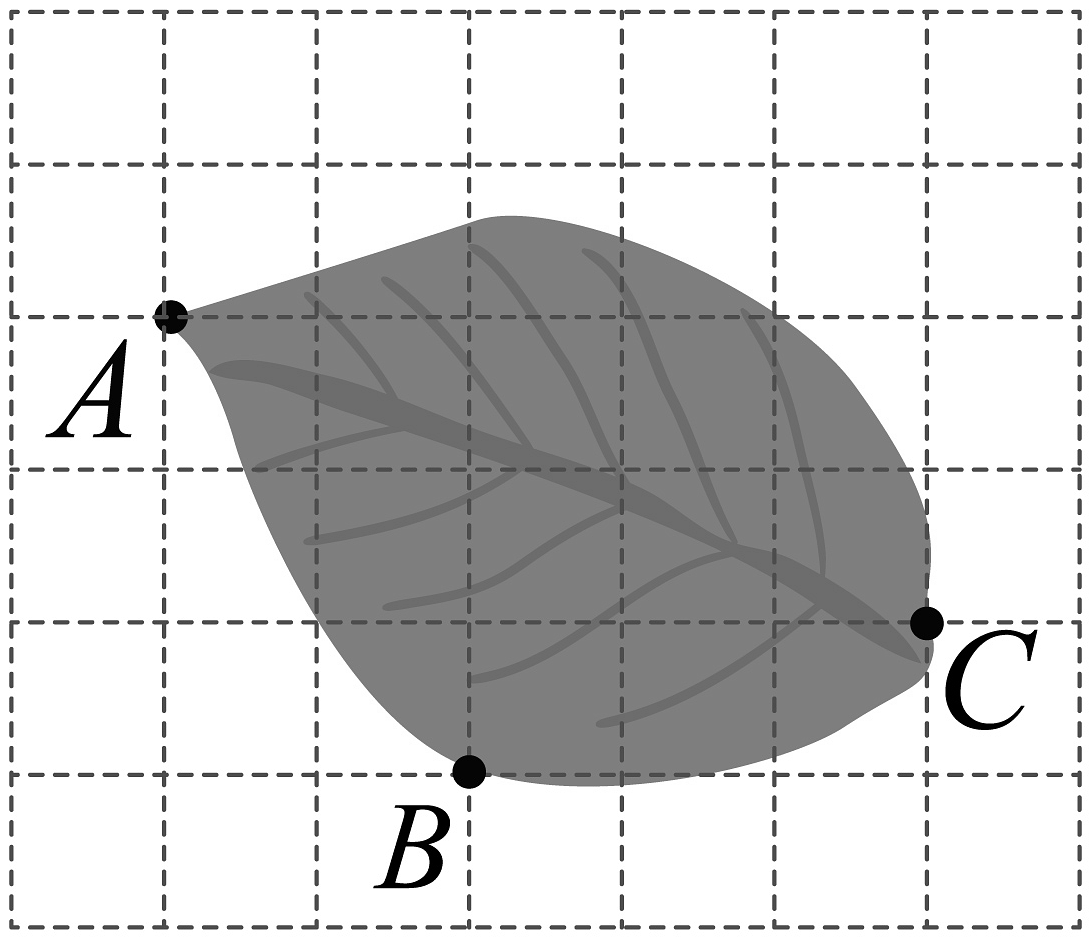
16、如图是一片树叶标本,将其放在平面直角坐标系中,表示叶片尖端A,B两点的坐标分别为 , 则叶柄底部点C的坐标为 .
-
17、在中, , , , 则 .
-
18、点向左平移2个单位后的坐标是 .
-
19、如图,E是的中点,平分 . 有下列结论:其中正确的是( )
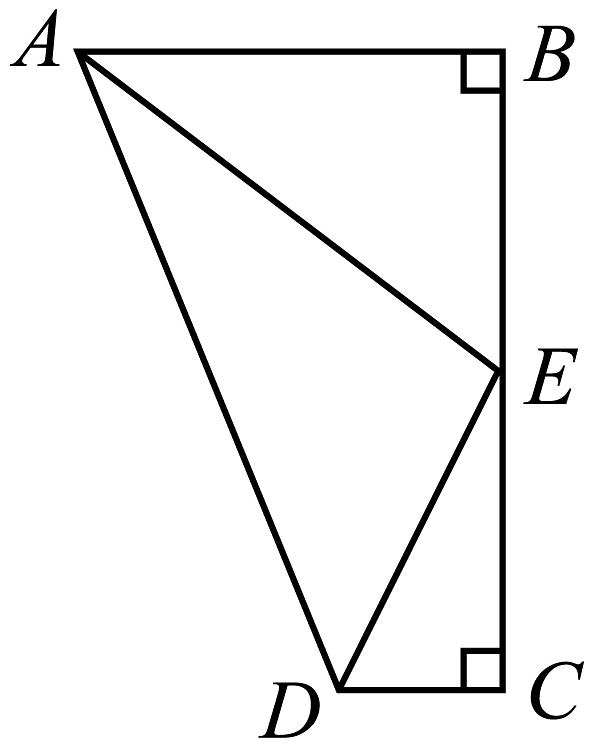 A、②③ B、①②④ C、②③④ D、①②③④
A、②③ B、①②④ C、②③④ D、①②③④ -
20、将点向右平移3个单位,再向上平移2个单位后的坐标是( )A、 B、 C、 D、