-
1、解下列方程:(1)、(2)、
-
2、 如图,在四边形ABCD中, , 点E是AD的中点,作于点F,已知 , , 则EF的长为.

-
3、 如图,矩形ABCD中,E为BC中点,将沿直线AE折叠,使得点B落在点F处,连接FC.若 , 则=.
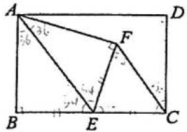
-
4、 数据1,3,5,12,a,其中整数a是这组数据中的中位数和众数,则该组数据的平均数是.
-
5、 如图,已知反比例函数的图象经过面积为8的矩形ABOC的顶点A,则k的值为.

-
6、 如果二次根式有意义,则的取值范围为.
-
7、 如图, 在▱ABCD中, AB=3, AD=4, , 过BC的中点E作 , 垂足为点F, 与DC的延长线相交于点H, 则的面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
8、 如图,矩形纸片ABCD中,点E是AD的中点,且 , BE的垂直平分线MN恰好过点C,则矩形的一边AB的长度为( )
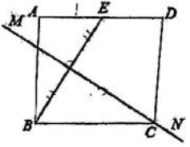 A、 B、 C、 D、2
A、 B、 C、 D、2 -
9、 用反证法证明命题“在直角三角形中,至少有一个锐角不大于时,首先应假设这个直角三角形中( )A、两个锐角都大于 B、两个锐角都小于 C、两个锐角都不大于 D、两个锐角都等于
-
10、 下列反比例函数图象一定在第一、三象限的是( )A、 B、 C、 D、
-
11、 下列图案中既是轴对称图形,又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
12、如图 1,在直角坐标系中,点 O 为坐标原点,点 A 在 x 轴的正半轴上,点 B 在 y 轴正半轴上, , , 以AB 为直径作 , AC 平分 交 于点 C,点 D 在 上且在第一象限,连接 CD,BD.
 (1)、 求 AB 的长.(2)、求证:.(3)、 当 时,求 的面积.(4)、 如图 2,射线 CD 交 OB 于点 G,交 x 轴正半轴于点 F,连接 AD,作点 F 关于 AD 的对称点 , 当点 落在 上时,求 OG 的长.
(1)、 求 AB 的长.(2)、求证:.(3)、 当 时,求 的面积.(4)、 如图 2,射线 CD 交 OB 于点 G,交 x 轴正半轴于点 F,连接 AD,作点 F 关于 AD 的对称点 , 当点 落在 上时,求 OG 的长. -
13、已知抛物线(b,c为常数)的图象经过点(1, 0)和(-3, 0).(1)、 求抛物线的表达式及对称轴.(2)、 过点A(0, t)与x轴平行的直线交抛物线于B,C两点(点B在点C的左侧),且 , 求t的值.(3)、 将抛物线沿x轴向左平移个单位长度,当时,平移后的抛物线函数值y的最大值与最小值的和为12,求m的值.
-
14、 阅读理解题:定义:如果一个数的平方等于-1,记为 , 这个数i叫做虚数单位
把形如 (a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加、减、乘法运算与整式的加、减、乘法运算类似.
例如计算: ,
,
, .
根据以上信息,完成下列问题.
(1)、 填空:.(2)、 计算:.(3)、 试一试:请利用以前学习的有关知识将化简成的形式. -
15、 如图,在▱ABCD中,对角线AC,BD交于点O,过点A作于点E,延长BC至点F,使 , 连接DF.
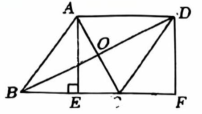 (1)、 证明:四边形AEFD是矩形.(2)、 若 , , , 求▱ABCD的面积.
(1)、 证明:四边形AEFD是矩形.(2)、 若 , , , 求▱ABCD的面积. -
16、如图1,点P在的平分线上,交AM于点B. 用尺规作图的方法作以AP为一边的等腰三角形.
小明:如图2,以A为圆心,AP为半径作弧,交AN于点D,连接PD,则是等腰三角形.
小华:以点A圆心,AB为半径作弧,交AN于点C,连接PC,则是等腰三角形.
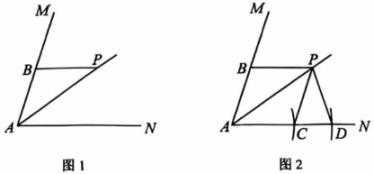 (1)、证明:小华所作的是等腰三角形.(2)、若 , 求的度数.
(1)、证明:小华所作的是等腰三角形.(2)、若 , 求的度数. -
17、某校为了解学生一周课外阅读情况,随机抽取部分学生调查了他们一周课外阅读时间,并将数据进行整理制成如下统计图. 请根据图中提供的信息,解答以下问题:
 (1)、 本次调查数据的中位数是小时.(2)、 抽查的这些学生一周平均的课外阅读时间是多少小时?(3)、 该校共有2400个学生,根据统计,估计该校学生一周课外阅读时间不少于4小时的人数.
(1)、 本次调查数据的中位数是小时.(2)、 抽查的这些学生一周平均的课外阅读时间是多少小时?(3)、 该校共有2400个学生,根据统计,估计该校学生一周课外阅读时间不少于4小时的人数. -
18、解方程:(1)、 .(2)、 .
-
19、(1)、计算:.(2)、化简:.
-
20、 在菱形ABCD中, , , E是AD延长线上的一点,连接BE,作与关于直线BE对称,连接AF,DF,则面积的最大值为.
