-
1、 如图,四边形ABCD内接于⊙O,AC为⊙O的直径,且∠ADB=∠CDB.
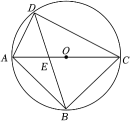 (1)、试判断△ABC的形状,并给出证明.(2)、若AB= , AD=1.
(1)、试判断△ABC的形状,并给出证明.(2)、若AB= , AD=1.①求线段DC的长.
②求的值.
-
2、 在的网格中,∆ABC的三个顶点都在格点上,我们把这种顶点在格点的三角形叫格点三角形,请按要求完成下列作图.
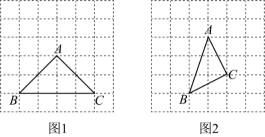 (1)、在图1网格中画出一个∆ADE,使 , 相似比为 , 且各顶点都在格点上.(2)、在图2的网格中作出与△ABC相似的最小格点△FGH.
(1)、在图1网格中画出一个∆ADE,使 , 相似比为 , 且各顶点都在格点上.(2)、在图2的网格中作出与△ABC相似的最小格点△FGH. -
3、 如图,在△ABC中,AD是△ABC的角平分线,点E是边AC上一点,且满足∠ADE=∠B.
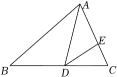 (1)、证明:△ADB∽△AED.(2)、若AB=9,AD=6,求AE的长.
(1)、证明:△ADB∽△AED.(2)、若AB=9,AD=6,求AE的长. -
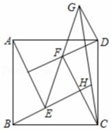
4、由四个全等的直角三角形和一个小正方形组成的大正方形ABCD如图所示.过点D作DF的垂线交小正方形对角线EF的延长线于点G,连结CG,延长BE交CG于点H.若AE=2BE,则的值
-
5、已知二次函数y=mx2+2mx+1(m≠0)在﹣2≤x≤2时有最小值﹣2,则m= .
-
6、如图,正六边形ABCDEF的边长为 , 以顶点A为圆心,AB长为半径画圆,则图中阴影部分的面积是 (结果保留π).
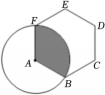
-
7、如图,△ABC与△DEF位似,点O为位似中心,且△DEF的面积是△ABC面积的9倍,则的值为

-
8、已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
x
…
3
4
5
6
7
8
…
y
…
﹣31
14
41
50
41
m
…
则表格中m的值是 .
-
9、某班级计划举办手抄报展览,确定了“5G时代”、“DeepSeek”、“豆包”三个主题,若小红随机选择其中一个主题,则她恰好选中“DeepSeek”的概率是 .
-
10、已知点A(﹣2,y1),B(1,y2)在抛物线y=3x2+bx+1上,若3<b<4,则下列判断正确的是( )A、1<y1<y2 B、y1<1<y2 C、1<y2<y1 D、y2<1<y1
-
11、如图,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置.过点A作AH⊥EF于点H,连接CH,若AD=3,DE=1,则CH的长为( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、如图,在直径BC为的圆内有一个圆心角为的扇形ABC.随机地往圆内投一粒米,该粒米落在扇形内的概率为( )
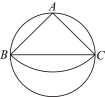 A、 B、 C、 D、
A、 B、 C、 D、 -
13、大自然鬼斧神工,一片小小的树叶,也蕴含着“黄金分割”的美.如图,P为线段AB的黄金分割点(AP>PB).如果AB的长度为10cm,那么AP的长度是( )
 A、 B、 C、6.18cm D、
A、 B、 C、6.18cm D、 -
14、 已知圆内接四边形中,::::则的大小是( )A、 B、 C、 D、
-
15、已知4x=3y(y≠0),则下面结论成立的是( )A、 B、 C、 D、
-
16、 如图,点E是正方形ABCD的BC延长线上一点,连接ED,过点B作交ED的延长线于点F,连接CF.
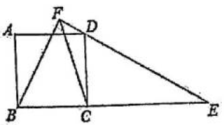 (1)、 若 , , 求BF的长;(2)、 求证:.
(1)、 若 , , 求BF的长;(2)、 求证:. -
17、 在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数的图象经过点B,过点B作轴于点C,点P是该反比例函数图象上任意一点.
 (1)、 求k的值;(2)、 若的面积等于2,求点P坐标.
(1)、 求k的值;(2)、 若的面积等于2,求点P坐标. -
18、 如图,AC,BD是四边形ABCD的对角线, , 分别是AD,BC的中点, , 分别是BD,CA的中点. 求证:EF,MN互相平分.
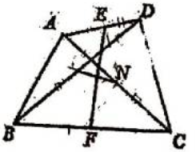
-
19、 据调查,八年级某班30名学生所穿校服尺寸绘制如下条形统计图:
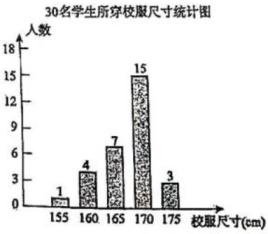 (1)、求这30名学生所穿校服尺寸的众数和中位数;(2)、若该校八年级共有600名学生,请你估计尺寸为170cm的校服需要多少件.
(1)、求这30名学生所穿校服尺寸的众数和中位数;(2)、若该校八年级共有600名学生,请你估计尺寸为170cm的校服需要多少件. -
20、 如图是由边长为1的小正方形构成的的网格,点A,B均在格点上.
 (1)、 在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、 在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上(画出一个即可).
(1)、 在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、 在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上(画出一个即可).