-
1、下列根式属于最简二次根式的是（ ）A、 B、 C、 D、
-
2、如图，在四边形ABCD中，AD//BC，AE⊥BC于点E，CF⊥AB于点F，AE与CF相交于点G，连接GD，已知∠1=∠2，∠3=∠4.
(1)、求证：四边形ABCD是平行四边形；(2)、若AG=3，DG=5，求GE的值；(3)、若F是AB的中点，连接EF，求证：DG⊥EF. -
3、某租赁公司拥有汽车100辆.据统计，当每辆车的月租金为3000元时，可全部租出.每辆车的月租金每增加50元，未租出的车将增加1辆.租出的车每辆每月的维护费为150元，未租出的车每辆每月只需维护费50元.(1)、当每辆车的月租金定为3600元时，能租出多少辆？(2)、当每辆车的月租金定为多少元时，租赁公司的月收益（租金收入扣除维护费）可达到306600元？
-
4、已知y与z成正比例，z与x成反比例.当x=-4时，z=3，y=-4.(1)、求y关于x的函数表达式；(2)、在平面直角坐标中，y关于x的函数图象上有A，B两点，且点A的横坐标为2，点B的横坐标为4，求OAB的面积.
-
5、如图，已知四边形ABCD是菱形，∠ABC=72°，以点A为圆心，AB为半径画弧线，分别交BC，CD于点F，E，连接AE，AF，EF，BD.
(1)、求∠EAF度数；(2)、求证：BD//EF. -
6、为了解某校八年级学生每周参加科学教育的时间（单位：h），随机调查了该校八年级a名学生，根据统计的结果，绘制出如下的统计图1和图2.
请根据相关信息，解答下列问题，
(1)、a= ， 图2中的m= ， 统计的这组学生每周参加科学教育的时间数据的众数和中位数分别为和.(2)、求统计的这组学生每周参加科学教育的时间数据的平均数；(3)、根据样本数据，若该校八年级共有学生600人，估计该校八年级学生每周参加科学教育的时间至少为9h的人数为多少？ -
7、在平面直角坐标系中， ， 是反比例函数的图象上两个点.(1)、求反比例函数解析式；(2)、判断A，B两点是否关于原点成中心对称，并说明理由.
-
8、解下列方程：(1)、x2=x；(2)、2x2+6x+3=0.
-
9、计算：(1)、(2)、
-
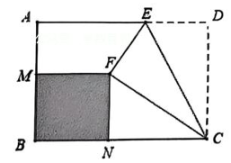
10、如图，在矩形ABCD中，AB=6，BC=8，点E是AD上一点，现将CDE沿CE翻折，得到△CEF.作FM⊥AB，FN⊥BC，当四边形MBNF是正方形时，则BN的值为.
-
11、方方参加“校园之声”歌唱比赛，其音准与节奏、音色与音质、表现力与情感表达的分数分别是90分、80分、80分.若将三项得分依次按2：5：3的权重确定最终成绩，则方方的最终成绩为分.
-
12、已知两个连续正奇数的积是143，设其中较小的正奇数是x，可列方程.
-
13、杭州雷峰塔其基座的平面示意图可抽象成八边形，如图所示，则这个八边形的内角和为.
-
14、化简=.
-
15、如图，在平行四边形ABCD中，对角线AC，BD相交于点O， ， 。过点A作BC的垂线交BC于点E，记 ， 。当x，y的值变化时，下列代数式的值不变的是（ ）
A、 B、 C、xy D、 -
16、若 ， ， （其中）都在反比例函数的图象上，则 ， ， 的大小关系是（ ）A、 B、 C、 D、
-
17、顺次连接一个四边形各边中点得到的四边形叫做这个四边形的中点四边形，如果一个四边形的中点四边形是矩形，那么原四边形的对角线需满足的条件是（ ）A、互相平分且相等 B、互相平分且垂直 C、相等 D、互相垂直
-
18、用反证法证明“ABC中至少有一个内角大于或等于60°”时，应先假设（ ）A、这个三角形中有一个内角大于60° B、这个三角形中有一个内角大于等于60° C、这个三角形中每一个内角都大于60° D、这个三角形中每一个内角都小于60°
-
19、函数y=的图象经过点（-4，6），则下列各点中在y=图象上的是（ ）A、（3，8） B、（-3，8） C、（-8，-3） D、（-4，-6）
-
20、某合唱团成员的平均年龄为52，方差为10，在人员没有变动的情况下，两年后这批成员平均年龄、方差分别是（ ）A、平均年龄为52，方差为10 B、平均年龄为54，方差为10 C、平均年龄为52，方差为12 D、平均年龄为54，方差为12