相关试卷

1、如图，一次函数 $y_{1} = a x + b$ ( $a \neq 0$ ， $b$ 为常数)的图象与反比例函数 $y_{2} = \frac{k}{x} (k \neq 0)$ 的图象交于点 $C (1, 6)$ ， $D (4, m)$ ，与坐标轴交于A，B两点.

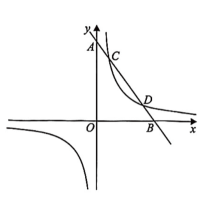
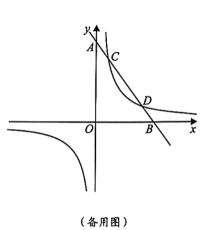(1)、求反比例函数表达式和m的值；

(2)、当 $0 < y_{1} < y_{2}$ 时，请直接写出x的范围；

(3)、若点E是第一象限内反比例函数图象上的一点，点F是x轴上的一点，当 $△ C E F$ 是以 $C F$ 为斜边的等腰直角三角形时，请求出点F的坐标.

查看解析
2、某商场销售一批服装，已知进价为150元/件，若以162元/件销售时，平均每天可销售100件.为了减少库存，商场决定降价销售.经调查发现，单价每降低1元，每天可多售出 20件.

(1)、若以158元/件销售，平均每天可销售多少件?

(2)、如果每天盈利1400元，单价应降低多少元?

(3)、如果每天想盈利2000元，能做到吗？若能，则此时应降低多少元；若不能，说明理由.

查看解析
3、如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ， $B E = D F$ ， $A E ⊥ B D$ ， $C F ⊥ B D$ ，垂足分别为点E，F.

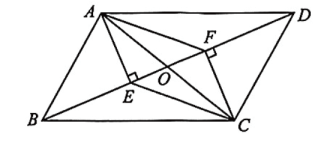(1)、求证：四边形 $A B C D$ 是平行四边形；

(2)、若点E，F是 $B D$ 的三等分点， $B D = 12$ ， $A C = 6$ ，求四边形 $A B C D$ 的面积.

查看解析
4、某同学进行社会调查，随机抽查了某小区的40户住户的年收入(万元)情况，并绘制了如图不完整的频数直方图（每组包括前一个边界值，不包括后一个边界值).

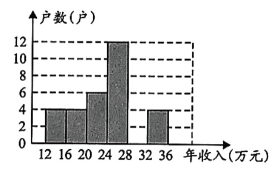(1)、求出年收入在“28-32”段的户数，并写出年收入的中位数落在哪一个收入段内?

(2)、如果每一组年收入均以最低计算，这40户住户的年平均收入至少为多少万元?

(3)、如果该小区有2000户住户，请你估计该小区有多少住户的年收入不低于28万元?

查看解析
5、如图是 $6 \times 6$ 的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，
$△ A B C$ 的三个顶点都在格点上.

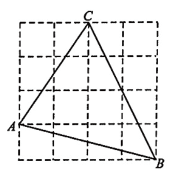(1)、只用无刻度的直尺，在给定的网格中画出BC边上的高线；

(2)、求BC边上的高线长.

查看解析
6、

(1)、计算： $\sqrt{3} \times \sqrt{6} - 2 \sqrt{\frac{1}{2}} + \sqrt{8}$

(2)、解方程： $x^{2} - 2 x - 15 = 0$

查看解析
7、如图，正方形纸片 $A B C D$ 的边长是 $4 c m$ ，三角板 $E F G$ 中， $∠ F = 9 0^{°}$ ， $∠ G = 3 0^{°}$ ， $E F =$ $2 \sqrt{3} c m$ .将三角板的顶点E固定在纸片的边AD上，边FG与纸片的边BC交于点H，则HG的最大值是cm.

查看解析
8、如图， $R t △ O A B$ 的直角顶点A在 $y$ 轴上，反比刨函数 $y = \frac{k}{x} (k > 0, x > 0)$ 的图象过线段 $O B$ 的中点 $D$ 、交线段AB于点C、连结 CD、若 $△ B C D$ 的面积为 $\frac{9}{2}$ ，则 $B C$ 的值为．

查看解析
9、一个多边形剪掉一个角后内角和为 $360 °$ ，则原多边形的边数为．

查看解析
10、如图，在 $△ A B C$ 中， $∠ B = 3 0^{°}$ 、 $∠ C = 4 5^{°}$ 、 $A C = 2$ ，则 $B C$ 的长为．

查看解析
11、一件原价为 $100$ 元的衣服经过两次降价后的价格为81元、若设每次降价的百分率都是.则可列方程为．

查看解析
12、使代数式 $\sqrt{x - 1}$ 有意义的：的取值范围是．

查看解析
13、如图，在 $▱ A B C D$ 中，对角线 $A C$ ， $B D$ 相交于点O， $A B = 3$ ， $B C = 4$ .记 $A C$ 长为 $x$ ， $B D$ 长为y，当x，y的值发生变化时，下列代数式的值不变的是（）

A、 $x + y$ B、 $y - x$ C、 $x y$ D、 $x^{2} + y^{2}$

查看解析
14、将3个相同的矩形按如图所示摆放在菱形 $A B C D$ 中，根据拼图可得以下三个结论：① $∠ B = 4 5^{°}$ ；②矩形长是宽的 $\sqrt{2}$ 倍；③当菱形面积为 $4 \sqrt{2}$ 时，则每个矩形的周长为6.上述结论中正确的有（）

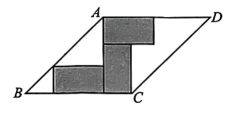A、① B、①② C、②③ D、①②③

查看解析
15、如图1，在矩形 $A B C D$ 中，要在边 $A D$ ， $B C$ 上找点 $E$ ， $F$ ，使四边形 $E B F D$ 为菱形，现有图2中的甲、乙两种方案，则正确的方案（）

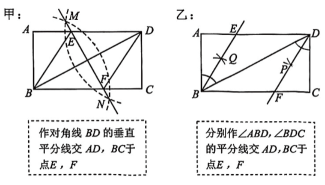A、甲、乙都是 B、只有甲才是 C、只有乙才是 D、甲、乙都不是

查看解析
16、已知蓄电池的电压 $U$ 为定值，使用蓄电池时；电流 $I$ (单位： $A$ )与电阻 $R$ (单位：Ω)是反比例函数关系： $I = \frac{U}{R}$ ．下列反映电流 $I$ 与电阻 $R$ 之间函数关系的图象大致是（）

A、 B、 C、 D、

查看解析
17、用反证法证明命题“四边形中至少有一个角是钝角或直角”是真命题时，第一步应假设（）

A、四边形中最多有一个钝角或直角 B、四边形中四个角全部是钝角或直角 C、四边形中至少有一个是锐角 D、四边形中没有一个角是钝角或直角

查看解析
18、某反比例函数图象上四个点的坐标分别为 $(x_{1}, 3)$ ， $(x_{2}, 2)$ ， $(2, - 3)$ ， $(x_{3}, - 2)$ ，则 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的大小关系为（）

A、 $x_{2} < x_{1} < x_{3}$ B、 $x_{1} < x_{2} < x_{3}$ C、 $x_{2} < x_{3} < x_{1}$ D、 $x_{1} < x_{3} < x_{2}$

查看解析
19、甲、乙、丙、丁四名运动员参加射击项目选拔赛，每人10次射击成绩的平均数（单位：环）和方差 $S^{2}$ 如下表所示：

甲
乙
丙
丁
$\bar{x}$
9.5
9.5
8.2
8.5
S²
0.09
0． 65
1.16
0.05
根据表中数据，从中选择一名成绩好且发挥稳定的运动员参加比赛，应该选择（）

A、甲 B、乙 C、丙 D、丁

查看解析
20、下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看解析

上一页 597 598 599 600 601 下一页跳转

	甲	乙	丙	丁
$\bar{x}$	9.5	9.5	8.2	8.5
S²	0.09	0． 65	1.16	0.05