-
1、据研究,忽略空气阻力,物体从高空下落的时间与下落高度近似满足公式 , 一物体从高空自由落下,则关于物体下落的时间 , 说法正确的是( )A、 B、 C、 D、
-
2、现有四批黄桃,从中各随机抽取40个,测量并计算得它们直径的平均数与方差如下:则这四批黄桃中果型较大且整齐的一批是( )
批次
甲
乙
丙
丁
平均数(单位:)
方差(单位:)
A、甲 B、乙 C、丙 D、丁 -
3、下列运算正确的是( )A、 B、 C、 D、
-
4、浙江交通物流发展良好,2024年全年完成综合客运量约570000000人次,其中数570000000用科学记数法表示为( )A、 B、 C、 D、
-
5、在这四个数中,最大的数是( )A、 B、0 C、 D、1
-
6、小刚和小聪同住一个小区,商量周日去体育场看一场足球赛.周日下午,小刚先出发去体育场,走了一段路后,在途中停下去便利店买水,后来发现球赛的时间快到了,就加快脚步走向体育场:小聪因家中有事迟出发,离家后跑步去体育场,如图所示:他们从家到体育场所走的路程S(米)与小刚离家时间t(分钟)之间的对应关系,根据图象回答下列问题:
 (1)、小刚家到体育场的路程是_________米,小聪比小刚早到体育场_________分钟;(2)、小刚出发几分钟后,小聪追上了小刚?(3)、体育场的球赛是下午 , 小刚在便利店买完水后如果还按原来走路的速度到体育场,是否会迟到?若迟到,请计算出迟到几分钟?若没迟到,请说明理由.
(1)、小刚家到体育场的路程是_________米,小聪比小刚早到体育场_________分钟;(2)、小刚出发几分钟后,小聪追上了小刚?(3)、体育场的球赛是下午 , 小刚在便利店买完水后如果还按原来走路的速度到体育场,是否会迟到?若迟到,请计算出迟到几分钟?若没迟到,请说明理由. -
7、计算:
-
8、如图,在矩形中, , , 点为中点,是线段上一动点,连接 , 把沿直线折叠得 , 连接并延长交直线于点 , 当最小时, .
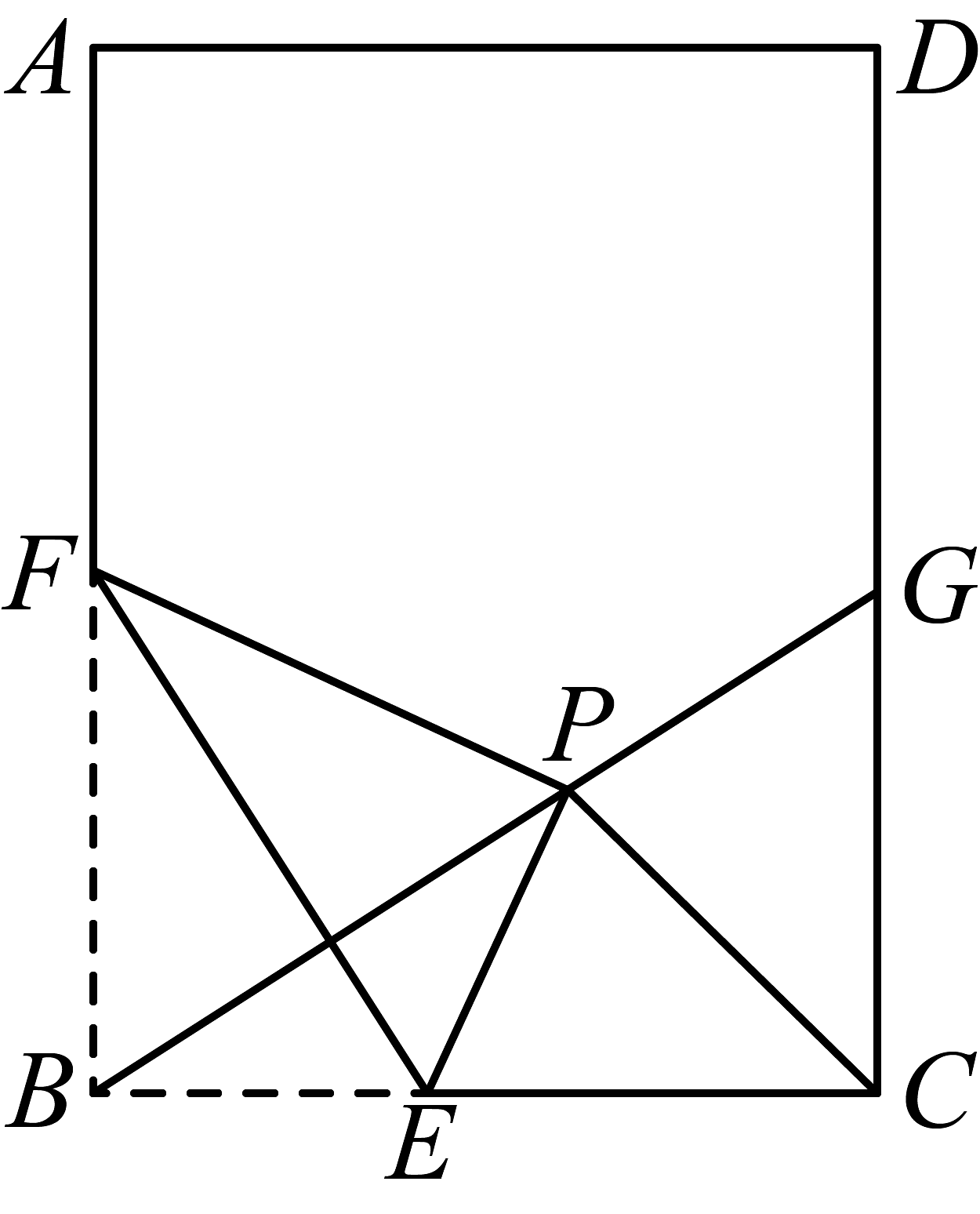
-
9、已知点在反比例函数的图像上.当时,的取值范围是 .
-
10、从“”中随机抽取一个字母,抽中字母的概率为 .
-
11、已知一个二次函数图象经过 , , , , 其中 , 则 , , 中最值情况是( ).A、最大,最小 B、最小,最大 C、最小,最大 D、最小,最大
-
12、2025年1月,福建新一轮以旧换新活动新增手机等数码产品购新补贴,将手机、平板电脑(含学习机)、智能手表手环等3类数码产品纳入补贴范围,最高补贴500元.某款学习机经过两次降价,单价由2400元降为1944元.若两次降价的百分率相同,设每次降价的百分率为 , 则符合题意的方程是( )A、 B、 C、 D、
-
13、为积极适应智能时代发展趋势,响应国家“人工智能+”行动战略部署,某校开展了以“人工智能在教育场景中的融合应用”为主题的比赛,其中六位参赛选手成绩的众数 , 其中五位参赛选手成绩分别为: , , , , , 则这组数据的中位数( )A、88 B、90 C、91 D、92
-
14、下列式子运算正确的是( )A、 B、 C、 D、
-
15、如图1,在中, , 点 , , 分别在边 , , 上, , .
 (1)、若 , 求的度数.(2)、如图2,当点与点重合时,求证:是的中点.(3)、如图3,作交边于点(点在点的左侧),猜想与的数量关系,并说明理由.
(1)、若 , 求的度数.(2)、如图2,当点与点重合时,求证:是的中点.(3)、如图3,作交边于点(点在点的左侧),猜想与的数量关系,并说明理由. -
16、已知抛物线(为常数)经过点 .(1)、用含的代数式表示 , 并求该抛物线的对称轴.(2)、当时, , 求抛物线的函数表达式.(3)、在(2)的条件下,已知点在抛物线上, , 求的取值范围.
-
17、如图,点在以为直径的半圆上,是的中点,连接分别交于点 .
 (1)、求证: .(2)、若 , 求的长.
(1)、求证: .(2)、若 , 求的长. -
18、实际应用:某工厂利用传送带运输产品,每个产品的质量为2千克.
素材一 如图,记电动机的输出功率为(瓦)、传送带的速度为、每个产品的质量为(千克)、产品的数量为(个),已知(为常数).
素材二 经测试,当传送带以0.5米/秒的速度运输10个产品时,电动机的输出功率为50瓦.
素材三 电动机的最大输出功率为200瓦.
 (1)、当传送带以1米/秒的速度运输15个产品时,求此时电动机的输出功率 .(2)、现将传送带的速度调整为0.8米/秒,求此时传送带最多能同时运输多少个产品?
(1)、当传送带以1米/秒的速度运输15个产品时,求此时电动机的输出功率 .(2)、现将传送带的速度调整为0.8米/秒,求此时传送带最多能同时运输多少个产品? -
19、如图1,直线 , 点分别在直线上,以点为圆心,长为半径作弧,交直线于点 , 以点为圆心,长为半径作弧,交直线于点 , 连接 .
 (1)、求证:四边形为菱形.(2)、如图2,作于点 . 若 , 求菱形的面积.
(1)、求证:四边形为菱形.(2)、如图2,作于点 . 若 , 求菱形的面积. -
20、某校在七、八年级开展汉字听写大赛,并从两个年级随机抽取了20名同学的成绩(单位:分),整理并绘制出如图所示的七年级成绩的频数分布直方图(每一组含前一个边界值,不含后一个边界值)和两个年级的成绩统计表.
七年级成绩的频数分布直方图

七、八年级成绩的统计表
年级
七年级
八年级
平均数
84
84
中位数
86
众数
85
已知七年级成绩在这一组的数据为:85 86 89 89 89 89 89 89 89
根据以上信息,回答下列问题:
(1)、表中___________,________(2)、根据以上统计量,你认为哪个年级的成绩较好?请说明理由.