-
1、 将方程写成用含x的代数式表示y的形式为( )A、 B、 C、 D、
-
2、 下列各数中,是无理数的是( )A、 B、 C、 D、
-
3、若式子在实数范围内有意义,则实数a的取值范围是( )A、 B、 C、 D、
-
4、若点的坐标是 , 则它到轴的距离是 .
-
5、如图,内接于 , 是的直径, , 是半径上的一点(不与点 , 点重合),连接并延长交于点 , 连接 , .
 (1)、求的度数.(2)、线段的延长线与线段的延长线交于点 .
(1)、求的度数.(2)、线段的延长线与线段的延长线交于点 .①求证: .
②设与交于点 , 当时,求的值.
-
6、已知二次函数 , 其图象抛物线与轴的交点坐标分别为 , , 且 .(1)、求当时,求抛物线的顶点坐标.(2)、若将抛物线向上平移1个单位后,与轴的交点坐标分别为 , 且 , 试判断与的大小,并说明理由.(3)、当时,的最大值与最小值之差为 , 求的值.
-
7、甲、乙两车沿同一条公路先后从城出发行驶去城,甲车匀速行驶1小时后休息半小时,继续以原来的速度匀速行驶,乙车匀速行驶的速度比甲车匀速行驶的速度快 , 甲、乙离开城的路程与甲车行驶时间之间的函数关系如图所示.根据图象信息解答下列问题:
 (1)、求乙车的速度.(2)、求线段所在直线的函数表达式.(3)、当乙车到达城时,甲车距离城的路程.
(1)、求乙车的速度.(2)、求线段所在直线的函数表达式.(3)、当乙车到达城时,甲车距离城的路程. -
8、小林解决如下问题有两种思路:
如图,在等腰中, ,
点是的中点,用尺规作图的方法
在上找一点 , 使得是的中位线.
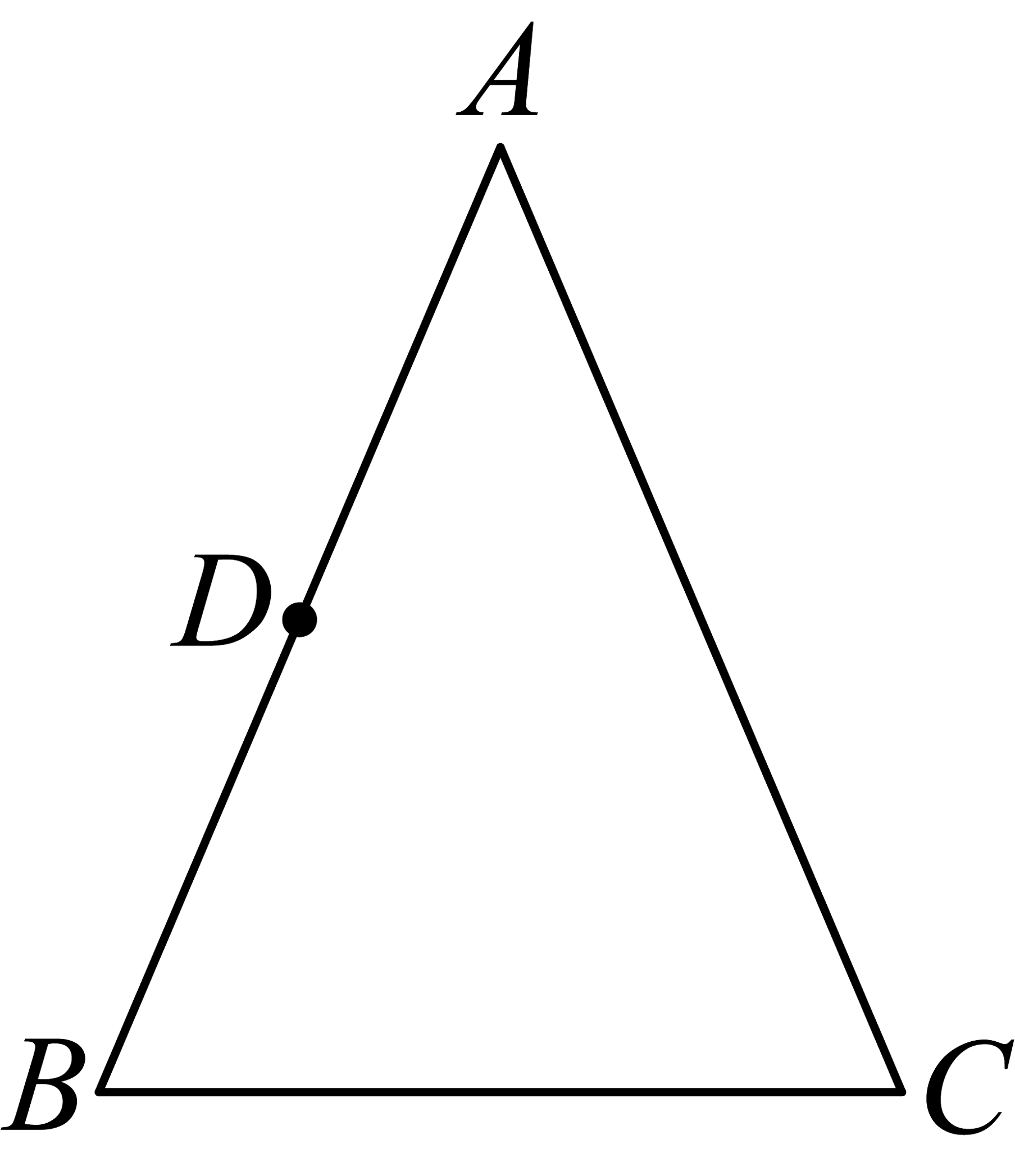
思路一:根据三角形中位线的定义,取的中点 , 连结 , 则是的中位线.
思路二:先在上找点 , 使 , 再在上找点 , 使 . 具体分两步,
步骤1:如图,分别以点 , 点为圆心,大于长为半径作弧,两弧相交于点 , 作直线交于点 .
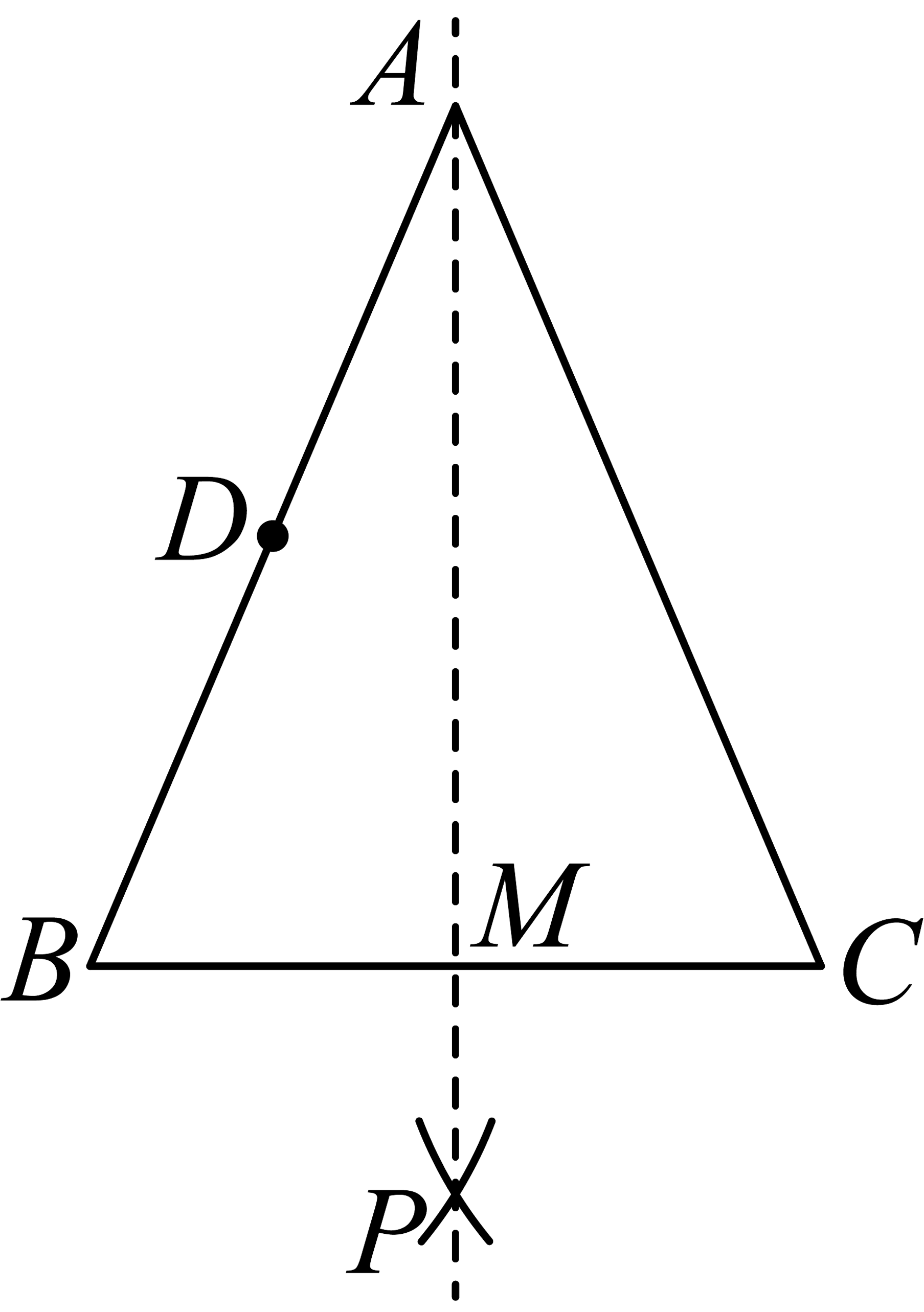 (1)、在图中连结步骤1里隐含的两条相等的线段,并证明 .(2)、小林给出的步骤2:“以点为圆心,长为半径作弧,交于点 , 连结 , 则是的中位线.”请指出步骤2中存在的问题.
(1)、在图中连结步骤1里隐含的两条相等的线段,并证明 .(2)、小林给出的步骤2:“以点为圆心,长为半径作弧,交于点 , 连结 , 则是的中位线.”请指出步骤2中存在的问题. -
9、中国的人工智能领域近年取得了显著的进展,并推动了技术在各行各业的普及和应用.某校采用抽样调查的方式对部分教师做了“我最常使用的软件”的问卷调查,并根据调查收集的数据,绘制了如下不完整的统计图:
 (1)、求抽样调查的教师人数,并补全条形统计图.(2)、该校共有教师240人,根据统计信息,估计该校教师最常使用“文小言”的人数.
(1)、求抽样调查的教师人数,并补全条形统计图.(2)、该校共有教师240人,根据统计信息,估计该校教师最常使用“文小言”的人数. -
10、如图,在中,对角线 , 相交于点 , 于点 , 于点 , 且 .
 (1)、求证: .(2)、当 , 时,求的值.
(1)、求证: .(2)、当 , 时,求的值. -
11、解方程组:
-
12、计算: .
-
13、如图,在菱形中,点是边上一点,将沿翻折,点恰好落在对角线上的点处,若此时 , 则的度数是 , 的值为 .

-
14、如图,在中, , , , 分别与 , 相切于点 , , 圆心在上,则的半径长为 .

-
15、在一个不透明的袋子中装有2个白球,个黑球,它们除颜色不同外,其余均相同.若从袋子中随机摸出一个球,它是白球的概率为 , 则 .
-
16、要使分式有意义,的取值应满足 .
-
17、如图,在矩形中, , 点是对角线上一动点,当时,过点作的垂线,分别交边于点 , 连结 , 下列三角形中与的面积之和不变的是( )
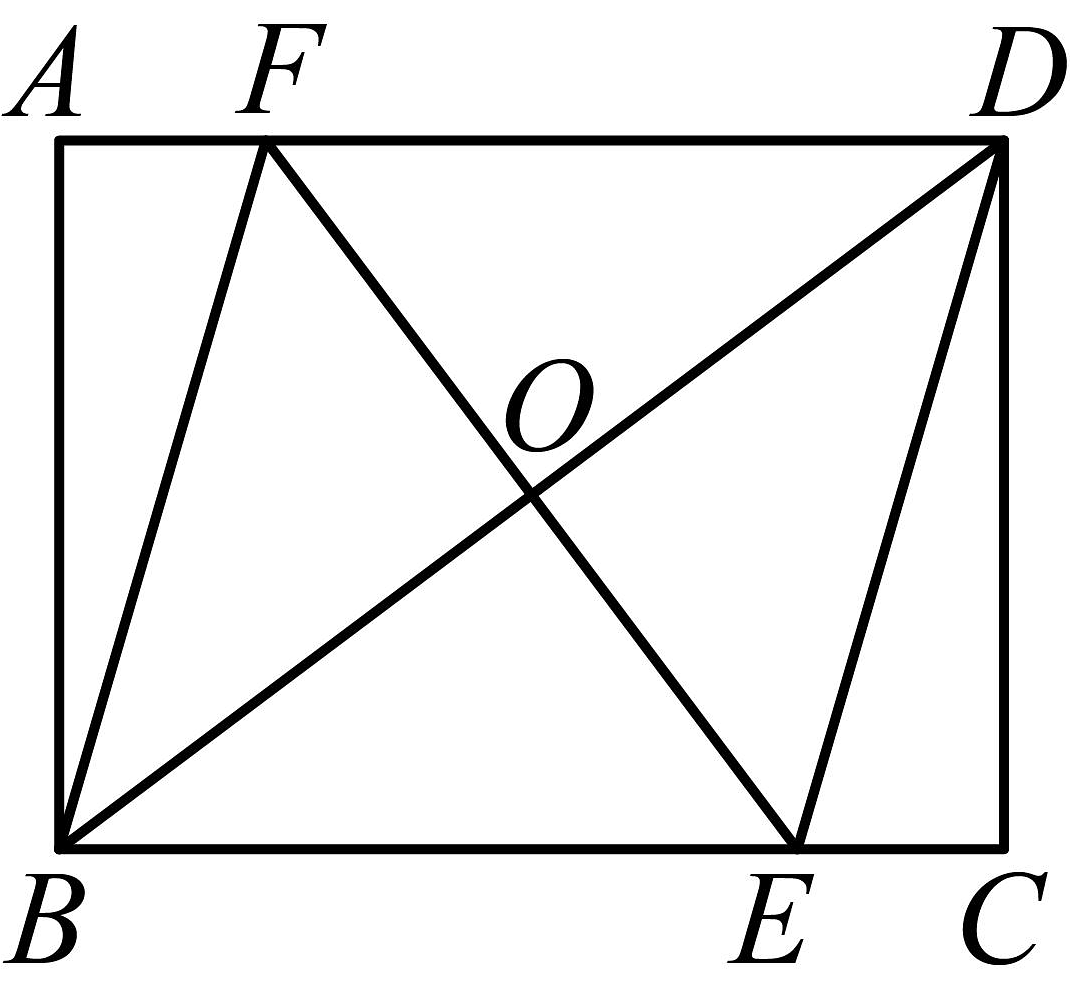 A、 B、 C、 D、
A、 B、 C、 D、 -
18、已知和两点在反比例函数的图象上,若 , 则的取值范围是( )A、 B、 C、 D、或
-
19、如图,在面积为20的正方形中, , 分别为 , 的中点,交于点 , 则的长为( )
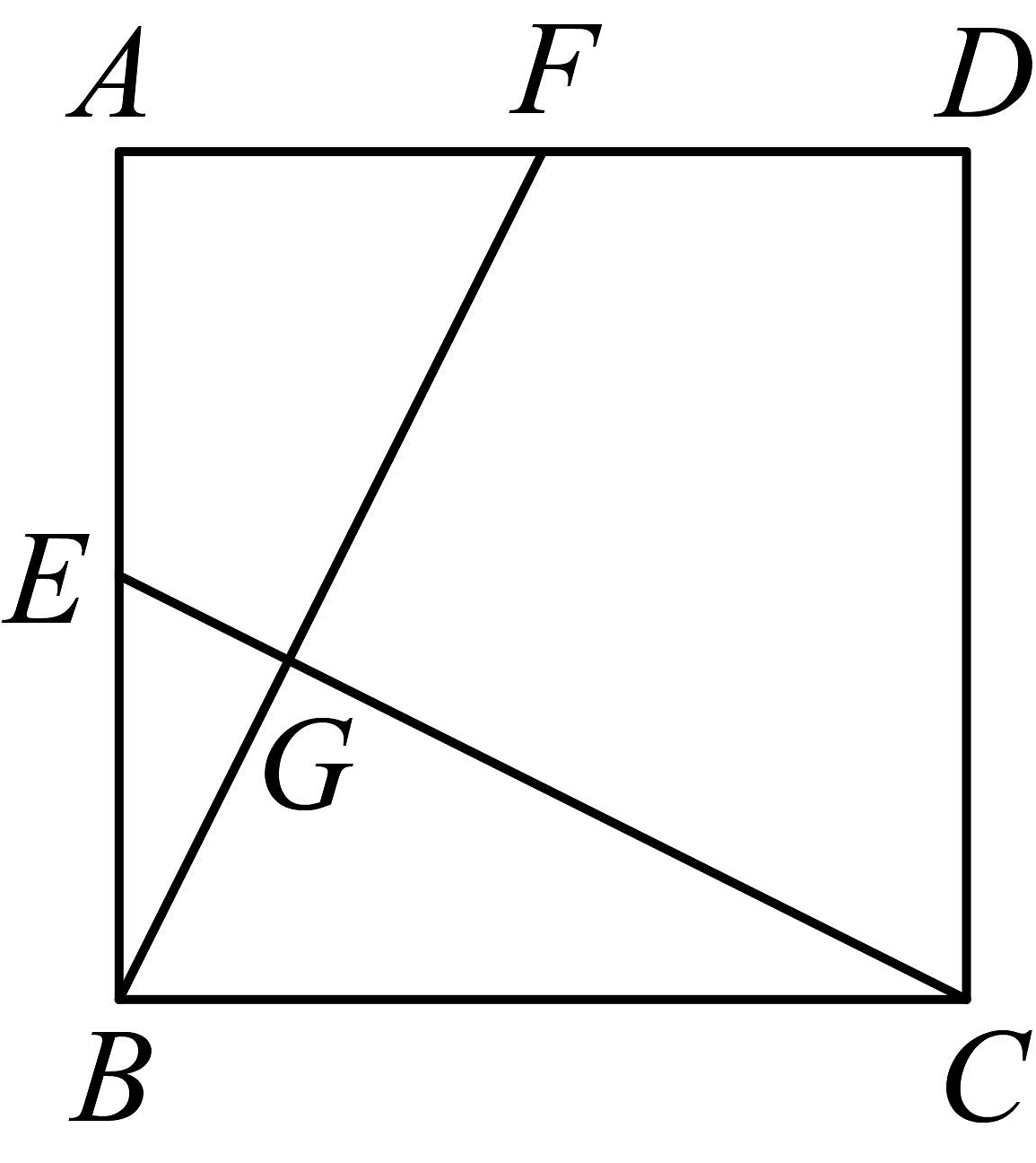 A、1 B、2 C、 D、3
A、1 B、2 C、 D、3 -
20、不等式组中,两个不等式的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、