-
1、计算:
-
2、如图,在平面直角坐标系中,点B的坐标为 , 点A是x轴正半轴上一动点,点P在第一象限, , , 点C的坐标为().
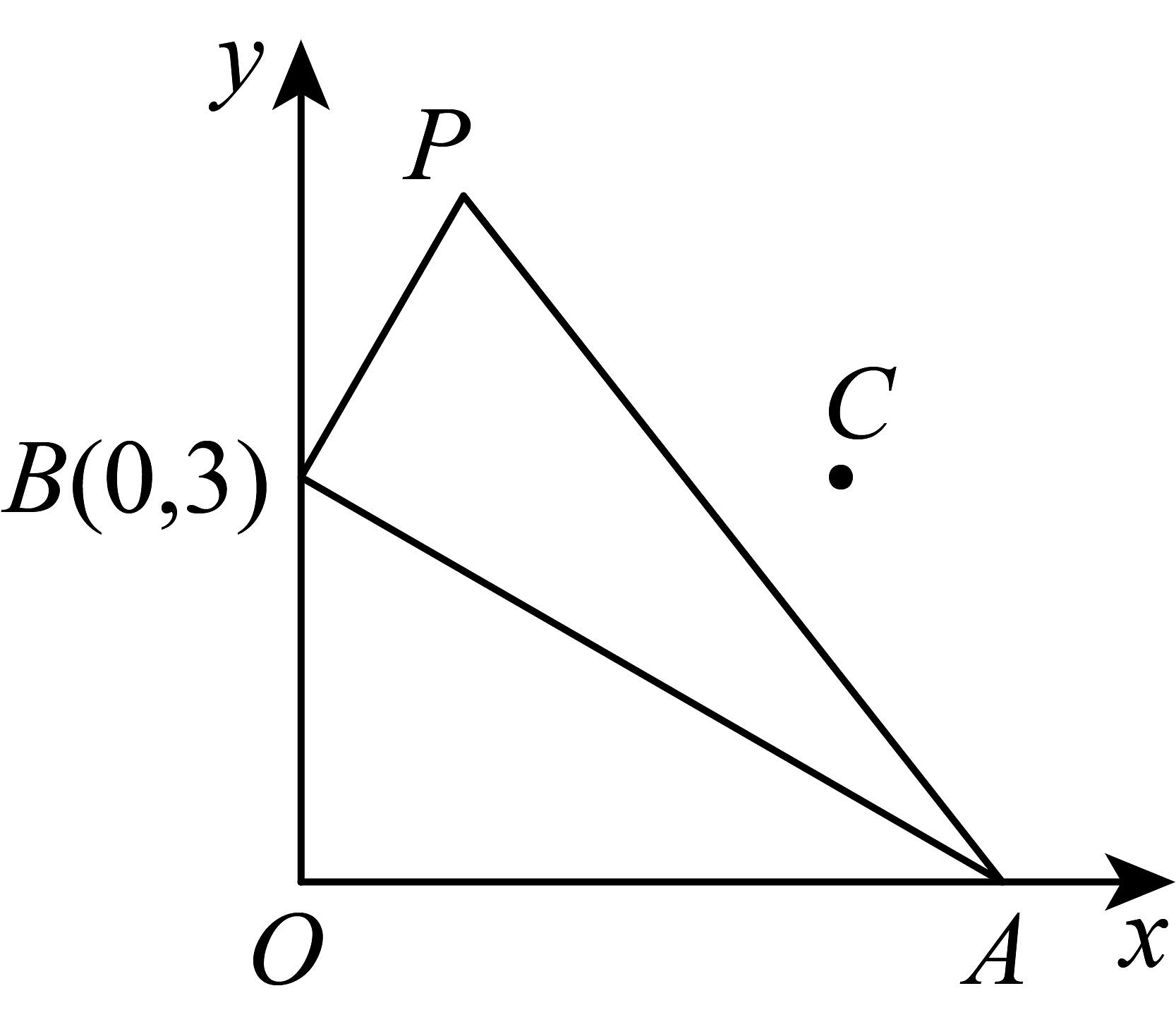
(1)若 , 则;
(2)连结 , 则的最大值为 .
-
3、已知点是反比例函数图象上一点,将点A向右平移2个单位,再向下平移4个单位后的点仍在这个反比例函数图象上,则 .
-
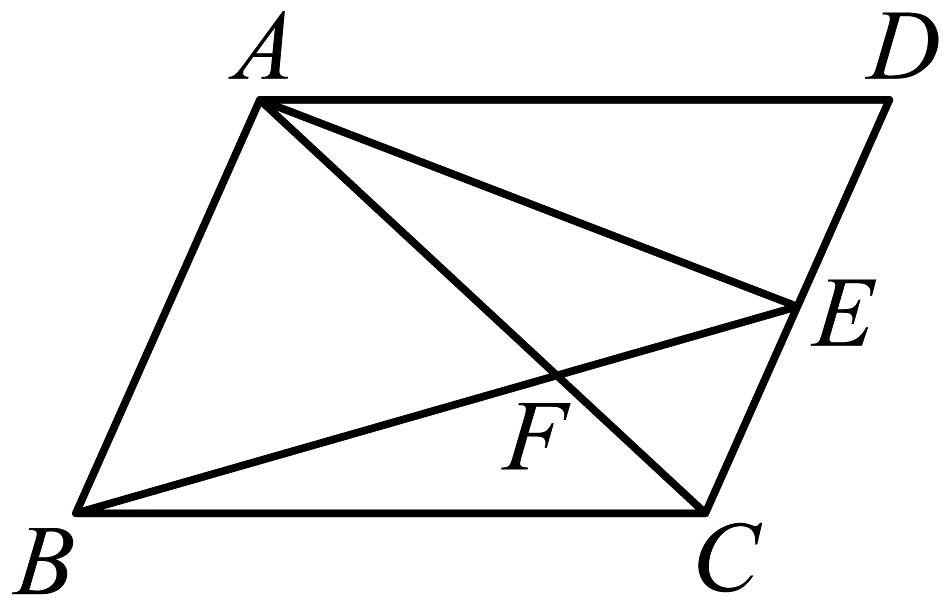
4、如图,在中,点是的中点,的面积为 , 则的面积为 .
-
5、若扇形的圆心角为 , 半径为8,则它的弧长为 .
-
6、如图,矩形中,点E是延长线上一点,且 , 连结 , 与交于点F,点G是的中点,连结 , 则下列比值为定值的是( )
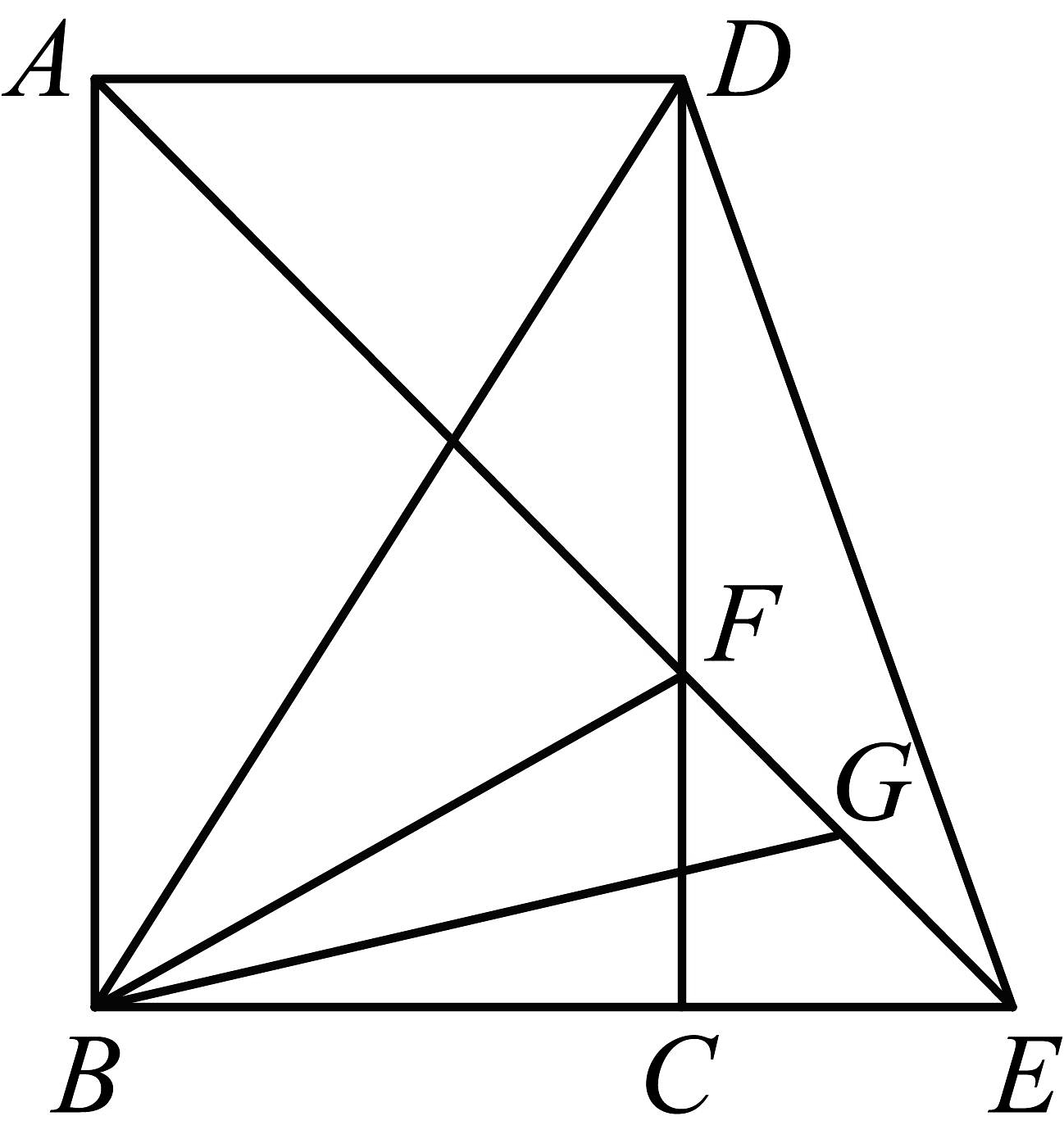 A、 B、 C、 D、
A、 B、 C、 D、 -
7、已知和均是关于x的一次函数,对于任意的实数a,b,当点在的图象上时,点就在的图象上,则称函数和具有性质P,以下函数和不具有性质P的是( )A、和 B、和 C、和 D、和
-
8、如图,在中, , , 点E是的中点,连接 , 且 , , 则( )
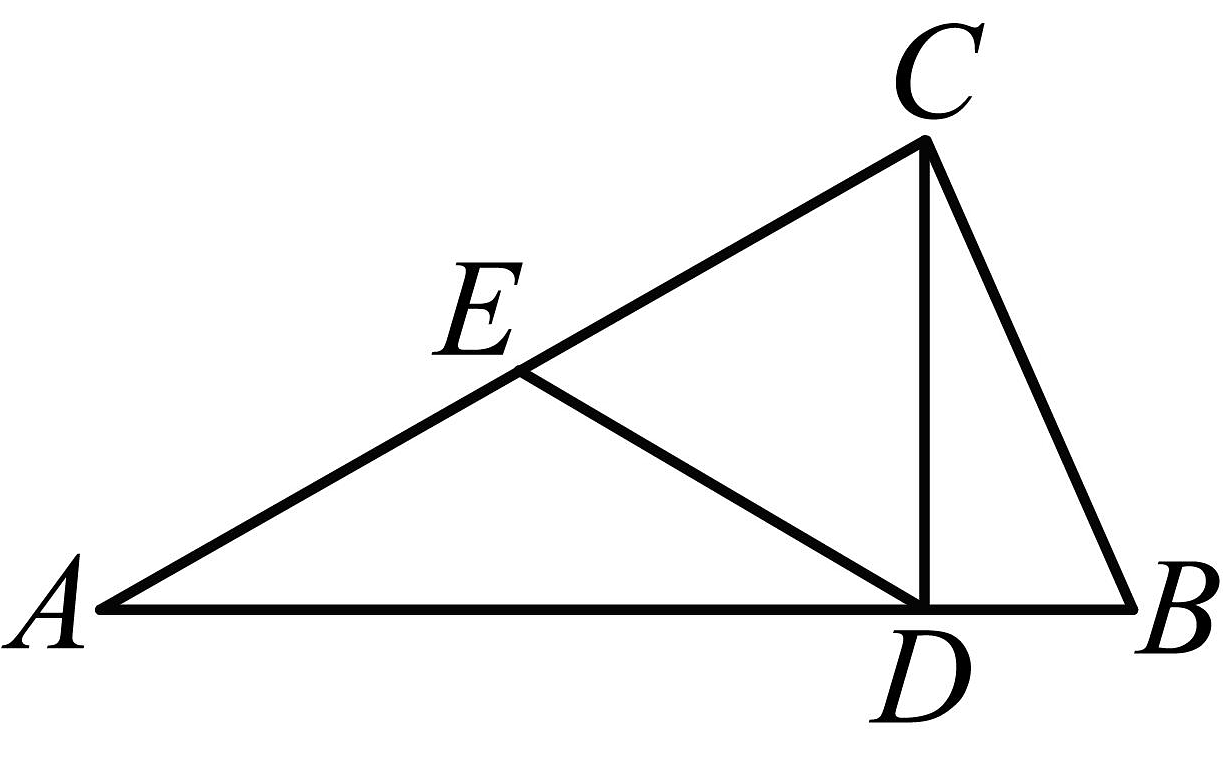 A、4 B、 C、 D、
A、4 B、 C、 D、 -
9、如图,点P在正方形的对角线延长线上,连接 , 过点P作交的延长线于点E,过点E作于点F.
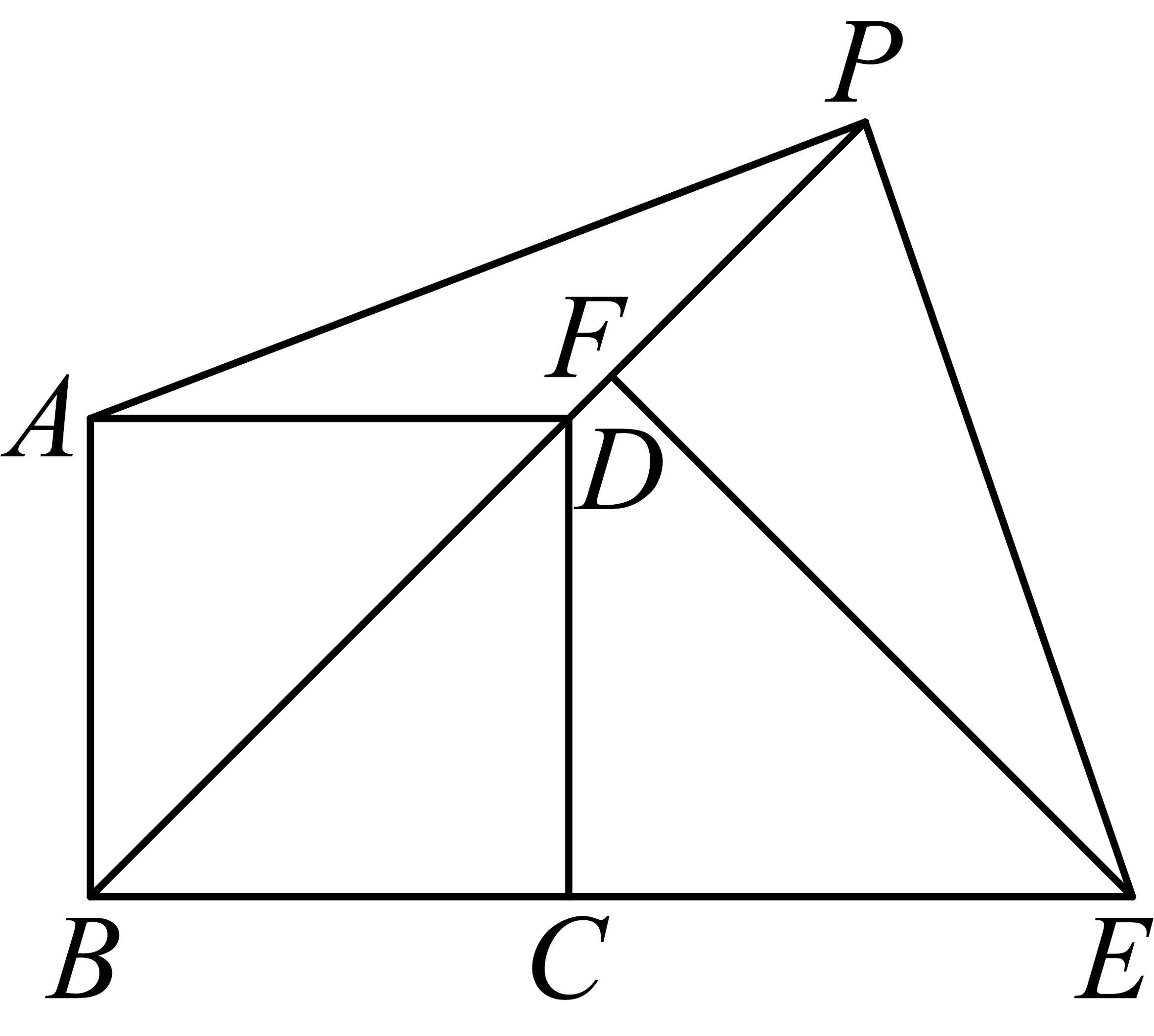 (1)、若 ,
(1)、若 ,①求的度数;
②设 , 求的长;
(2)、求证: . -
10、已知二次函数的顶点横坐标比二次函数(a为常数)的顶点横坐标大1.(1)、求a的值;(2)、二次函数(a为常数)的图象是否可以由平移得到?如果可以,请说出平移方案;如果不可以,请说明理由.(3)、设点在抛物线上,点在抛物线上.若 , 且 , , 求n的值;
-
11、先阅读,后完成:在数学复习课上,某老师出了一道题如下:
如图,已知中, . 求证: ,
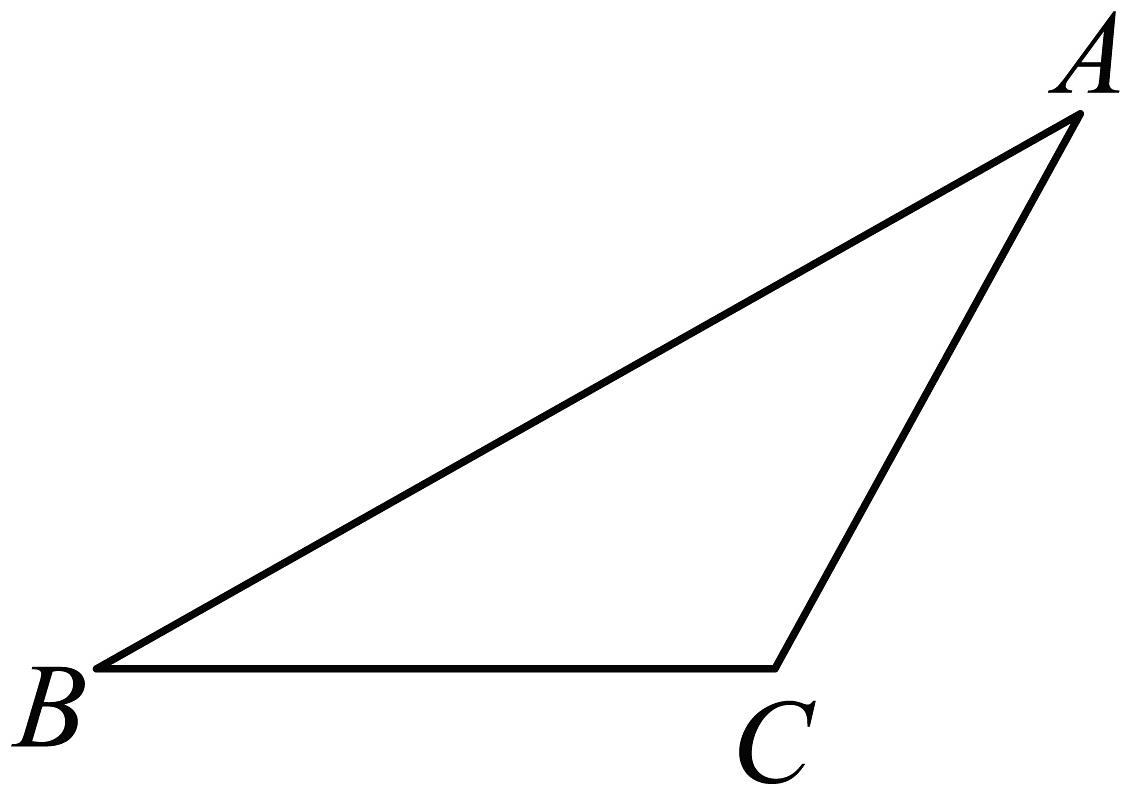
小丽与小明思考后,有一段交流对话:
小明:这是一个假命题,因为根据三角函数的定义,图中没有直角三角形,所以结论不成立.
小丽:我可以过某一个点作出垂线段,产生直角三角形,就可以证明了.
小明:哦……我明白了!
(1)、请你完成小丽的证明过程.(2)、已知 , , 求的面积. -
12、小西和小湖两人从同一地点出发跑步前往某风景区游览,小西全程匀速跑,5分钟后小湖才开始出发,第一次与小西相遇时,原地休息片刻,第二段速度比第一段速度提高30米/分钟,结果小湖比小西提前4分钟到达.小西和小湖的行程相关信息如表所示;离出发地的距离(米)与小西、小湖跑步时间(分)的函数关系如图所示.
时间
里程分段
行程里程(米)
小西
-
不分段
5400
小湖
-
第一段(休息前)
1800
休息
第二段(休息后)
3600
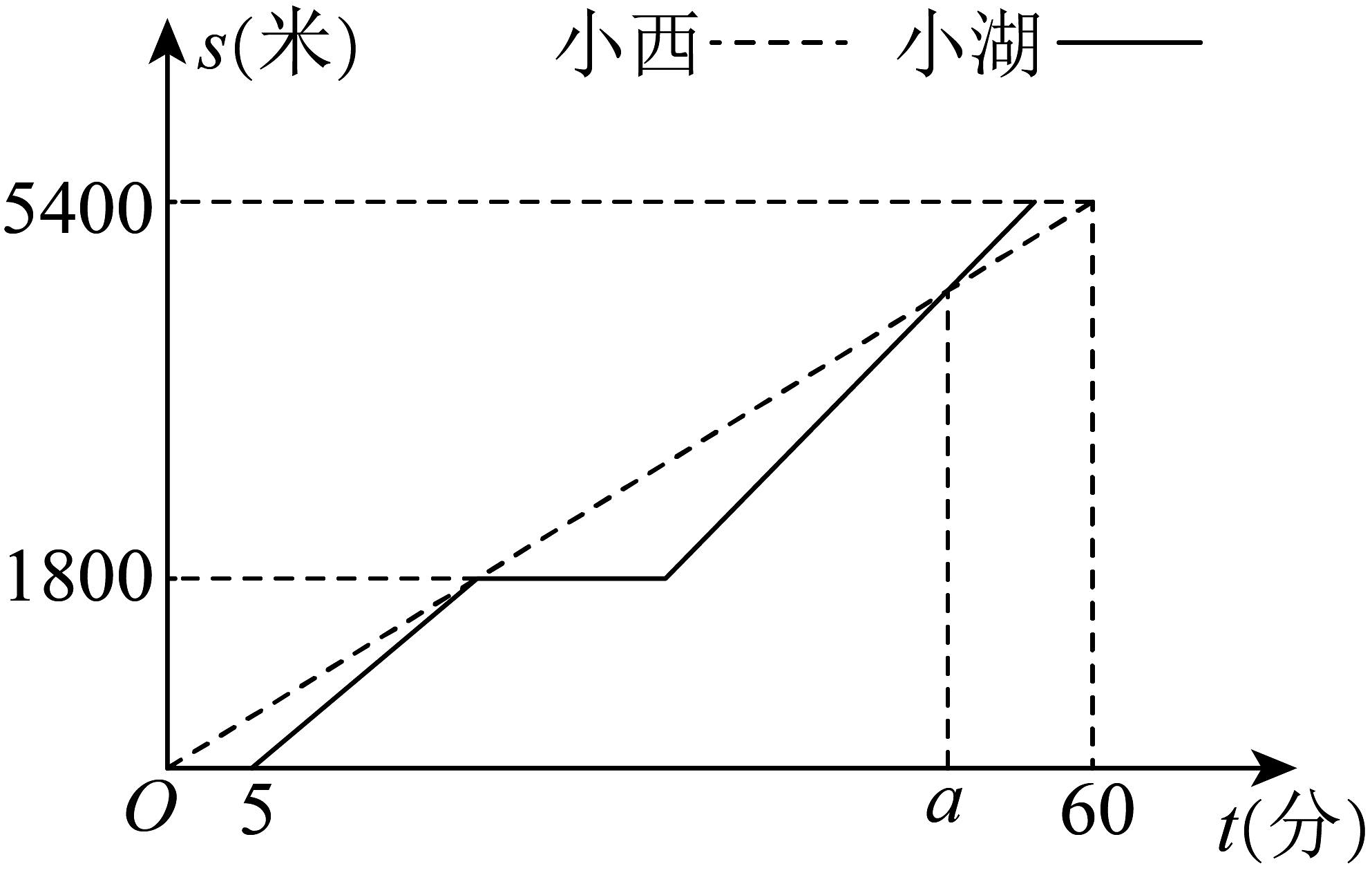 (1)、分别求出小西匀速和小湖第一段的跑步速度.(2)、求小湖中间休息的时间.(3)、在a分钟时两人第二次相遇,求a的值.
(1)、分别求出小西匀速和小湖第一段的跑步速度.(2)、求小湖中间休息的时间.(3)、在a分钟时两人第二次相遇,求a的值. -
13、随着科技的进步和网络资源的丰富,在线学习已成为更多人的自主学习选择.某校计划为学生提供以下四类在线学习方式:在线阅读、在线听课、在线答题和在线讨论.为了解学生需求,该校随机对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查(不可多选,也不可不选),并根据调查结果绘制成如下两幅不完整的统计图,根据图中信息,解答下列问题:
 (1)、直接写出本次调查的学生总人数____;(2)、补全条形统计图;(3)、该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生有多少人?
(1)、直接写出本次调查的学生总人数____;(2)、补全条形统计图;(3)、该校共有学生3000人,请你估计该校对在线阅读最感兴趣的学生有多少人? -
14、如图,已知E、F分别是的边、上的点,且 .
 (1)、求证:四边形是平行四边形;(2)、若 , 平分 , 且 , 求的长.
(1)、求证:四边形是平行四边形;(2)、若 , 平分 , 且 , 求的长. -
15、解不等式组: .
-
16、计算: .
-
17、如图,在菱形中, , 点E关于的平分线的对称点为F,点F关于的平分线的对称点为G,连接 . 若 , , 则= .

-
18、将、、、写在四张完全相同且不透明卡片的正面,把四张卡片背面朝上,洗匀后放在桌面上,从中随机抽取一张卡片,恰好抽到y随x的增大而减小的概率是 .
-
19、解方程: , 则方程的解是 .
-
20、已知中,弦垂直弦 , , , 则关于直径的说法正确的是( )A、一定等于 B、可能大于 C、不可能大于 D、不可能等于