-
1、电影《哪吒之魔童闹海》上映10天突破60亿票房,成为中国电影票房榜冠军.为了解大家对电影的评价情况,小舟同学从某电影院观影后的观众中,随机抽取部分观众对电影进行评价,并对评分(十分制)进行统计整理,所有观众的评分均高于8分(电影评分用x表示,共分成四组:A.;B.;C.;D.),下面给出了部分信息:
C组的数据是:9.1,9.2,9.3,9.3,9.3,9.3,9.4,9.4.
 (1)、求出C组数据的中位数和众数;(2)、补全条形统计图;(3)、若共有800名观众参加了此次评分调查,估计此次评分调查认为电影特别优秀()的观众人数是多少?
(1)、求出C组数据的中位数和众数;(2)、补全条形统计图;(3)、若共有800名观众参加了此次评分调查,估计此次评分调查认为电影特别优秀()的观众人数是多少? -
2、小张在学习分式时,不确定自己做的练习是否正确,于是请教了强大的软件,请你仔细阅读小张的解答过程,并补充完整的分析.

先化简,再求值 , 其中
解:原式①
②
③
当时
原式
,
编辑
我的解答正确吗?
豆包给出分析:
这个解答从第______步开始出现错误;虽然最终答案是0,但过程存在逻辑错误.
正确解答为: , 其中 ,
解:原式 .
-
3、(1)计算:
(2)化简:
-
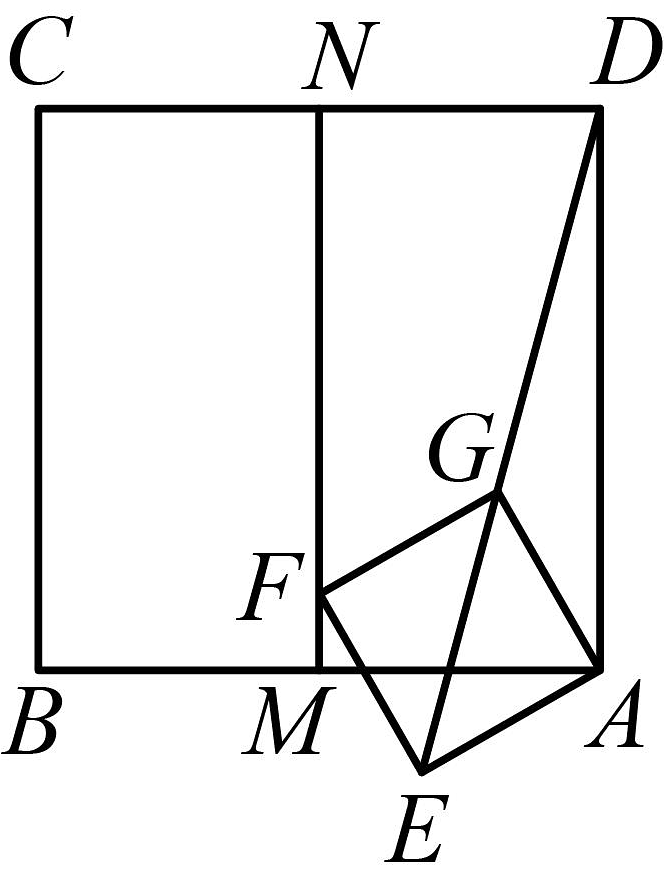
4、如图,在中, , , 点D为边上一点,连结 , 作点B关于的对称点E,连结 , 延长交于点F,若 , 则 .
-
5、已知点在直线(b为常数)上,若的最小值为 , 则 .
-
6、已知圆锥的侧面展开图是半径为 , 圆心角为的扇形,则圆锥的侧面积是 .
-
7、如图,在矩形中,E、F分别为、上的点,且 , 连结 , 其中 , , 则( )
 A、 B、3 C、 D、
A、 B、3 C、 D、 -
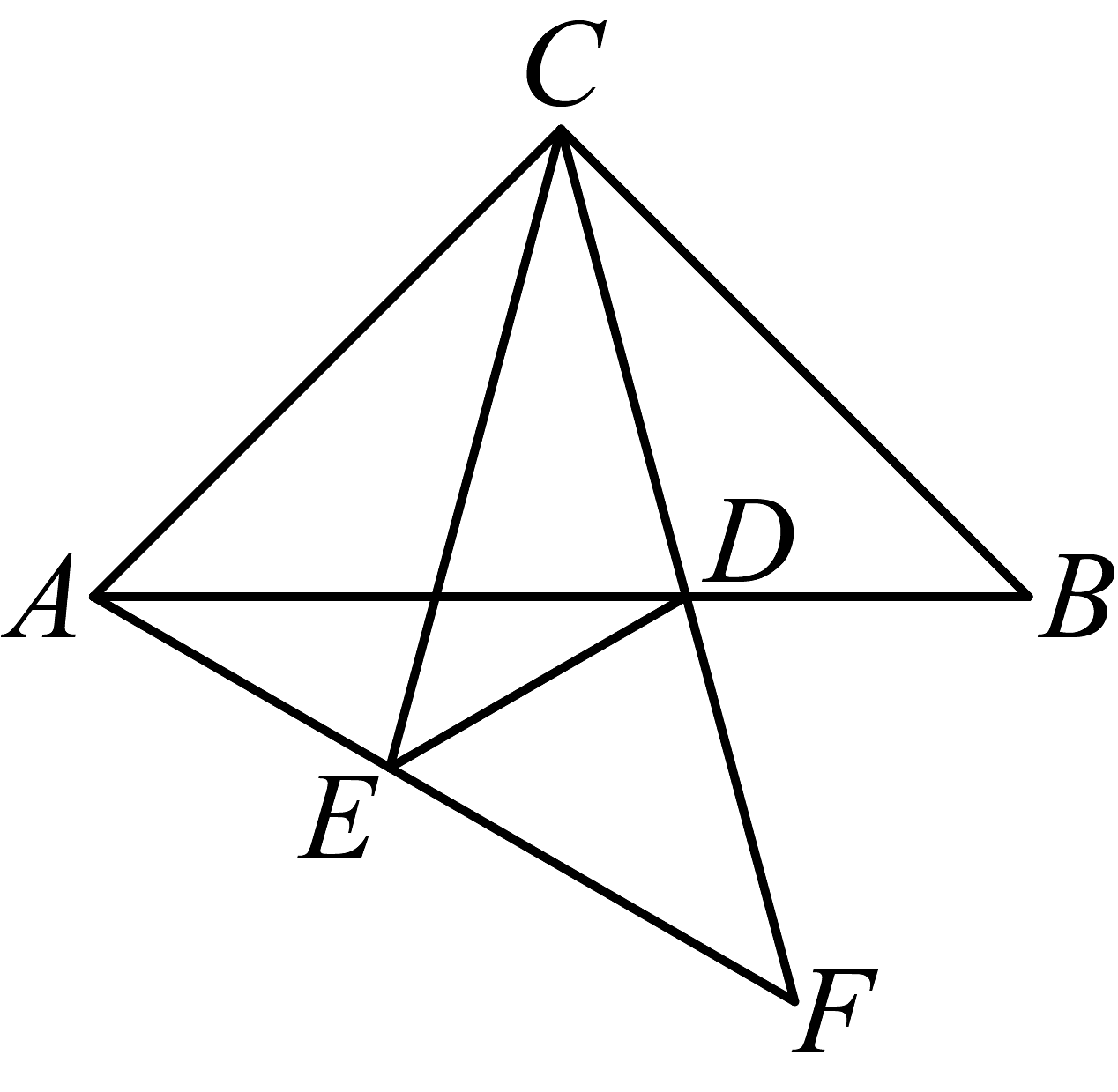
8、如图,在中,点D在边上,点E在边上, , , 若要求的度数,则只需知道( )的度数
 A、 B、 C、 D、
A、 B、 C、 D、 -
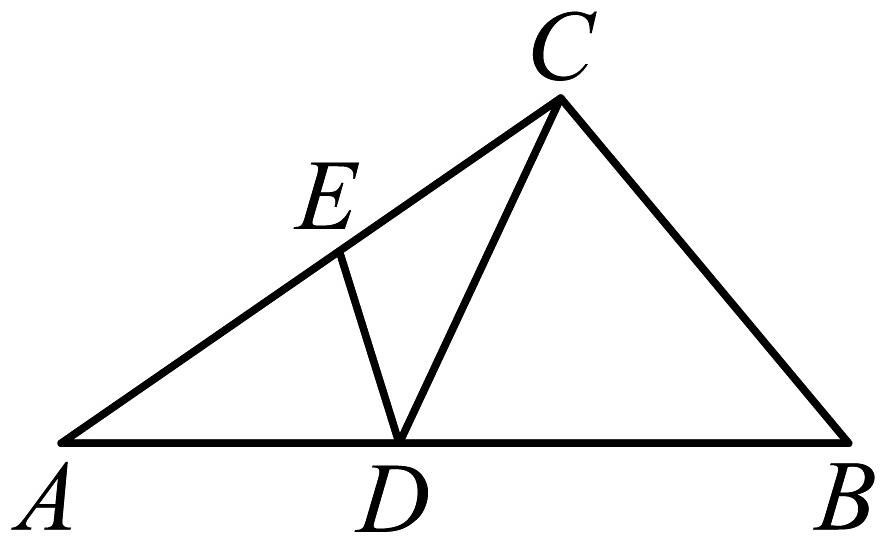
9、如图,在中, , 以点为圆心,适当长为半径画弧,分别交于点M,点 , 再分别以为圆心,大于的长为半径画弧,两弧交于点 , 射线与交于点D, , 垂足为 . 若 , 则( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4 -
10、如图,与位似,位似中心为点O, , 的面积为4,则面积为( )
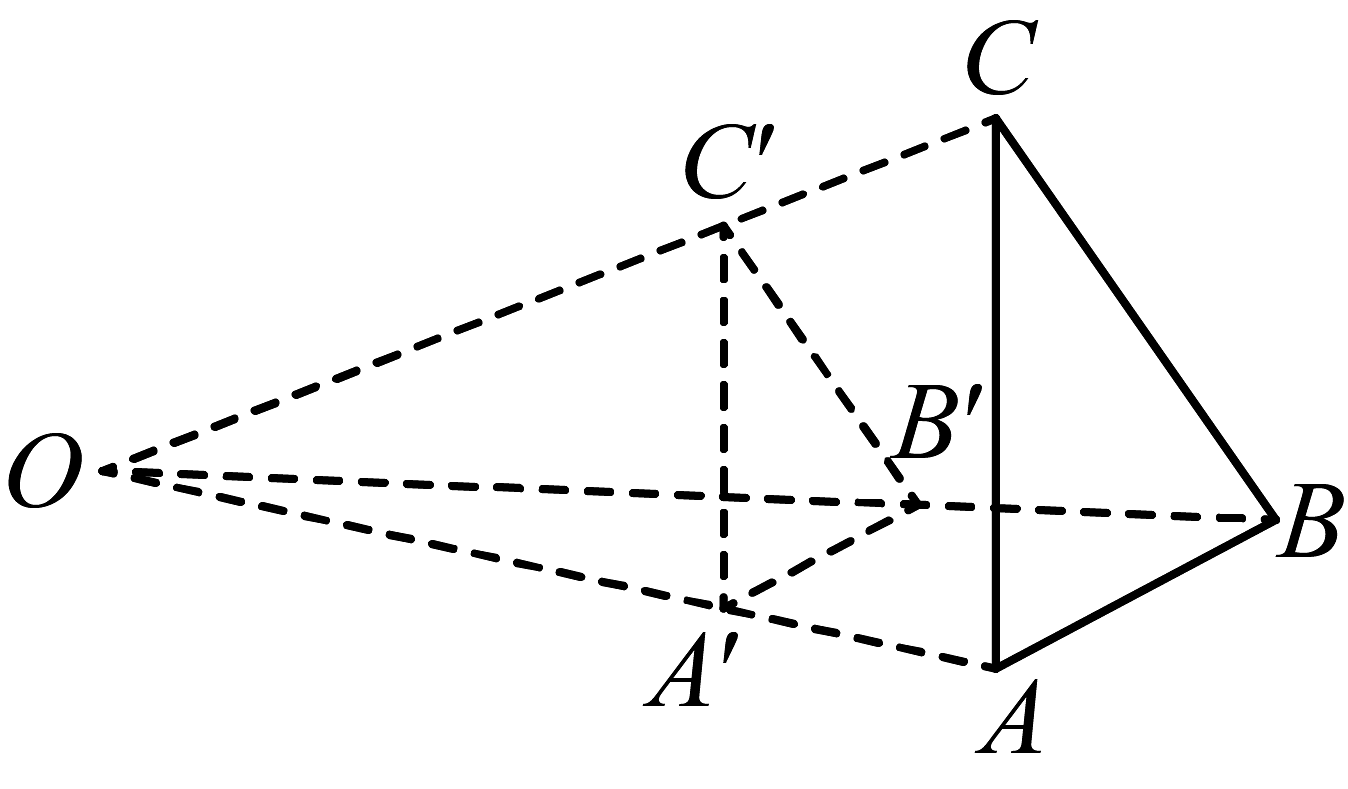 A、6 B、7 C、8 D、9
A、6 B、7 C、8 D、9 -
11、小明同学在学习了八年级上册“三角形”、“特殊三角形”两堂课后,发现学习内容是逐步特殊化的过程,于是便整理了如图,那么下列选项不适合填入的是( )
 A、两边相等 B、一个角为直角 C、有一个角 D、斜边与直角边比为
A、两边相等 B、一个角为直角 C、有一个角 D、斜边与直角边比为 -
12、2025年“体重管理年”正式启动,其中所涉及的体质指数“”是衡量人体胖瘦程度的标准,其计算公式为(m表示体重,单位:公斤;h表示身高,单位:米),成年人数值标准见表:
BMI范围
胖瘦程度
偏瘦
正常
偏胖
肥胖
已知某位成年人身高1.6米,体重64公斤,则该成年人胖瘦程度为( )
A、偏瘦 B、正常 C、偏胖 D、肥胖 -
13、下列运算正确的是( )A、 B、 C、 D、
-
14、如图1,在中,是钝角,以为直径的圆与边交于点D,与延长线交于点E,连结 , 连结交于点G.
 (1)、求证: .(2)、记与之间是否存在确定的数量关系?若存在,请求出该数量关系;若不存在,请说明理由.(3)、如图2,若点G关于的对称点在以为直径的圆上,证明点G是的内心.
(1)、求证: .(2)、记与之间是否存在确定的数量关系?若存在,请求出该数量关系;若不存在,请说明理由.(3)、如图2,若点G关于的对称点在以为直径的圆上,证明点G是的内心. -
15、提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当时,车流速度v是车流密度x的一次函数.
(1)当时,求车流速度v关于x的解析式;
(2)当车流密度x为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/时,)可以达到最大,并求出最大值.(精确到1辆/小时)
-
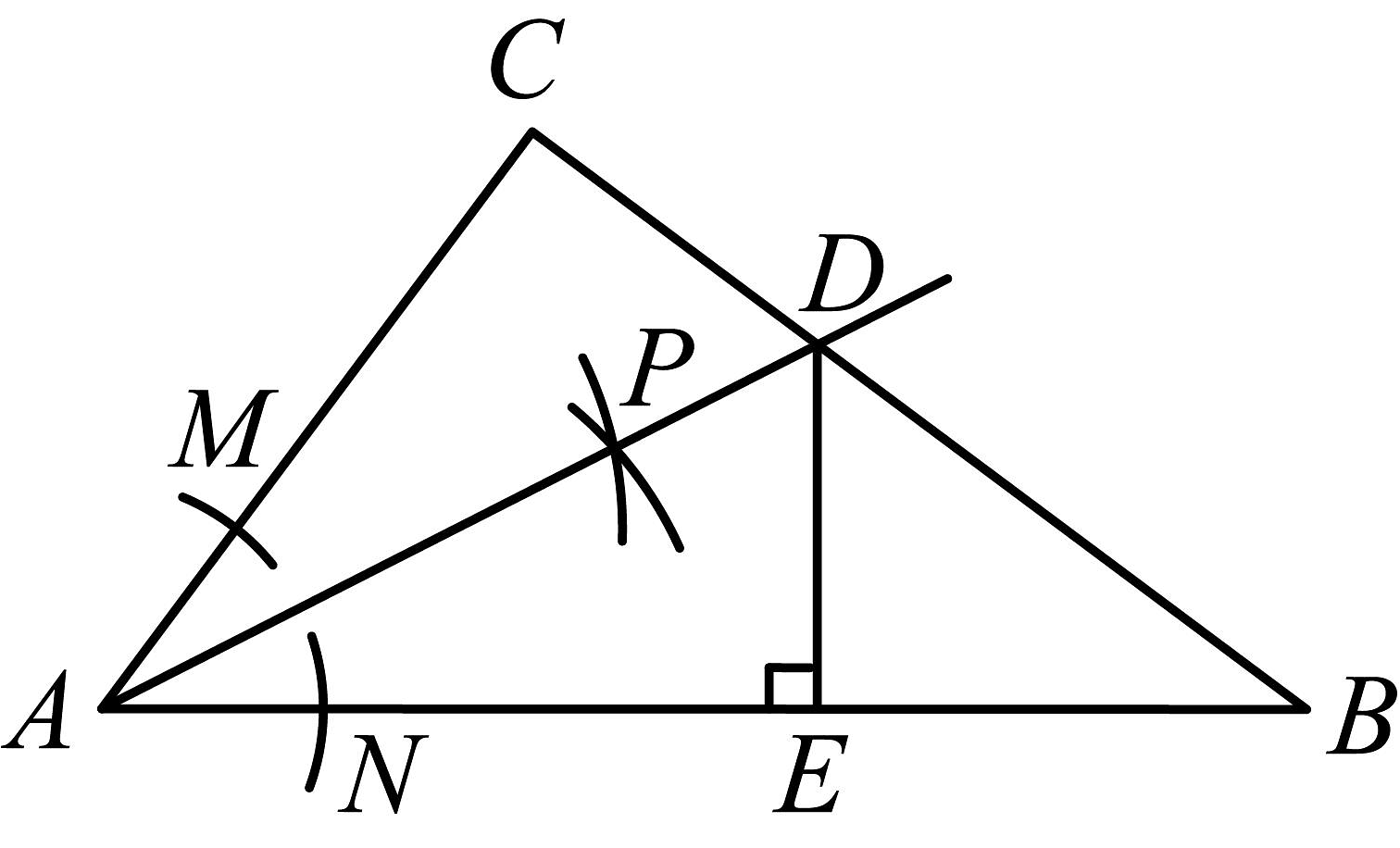
16、课本56页中有这样一道题:证明.如果两个三角形有两条边和其中一边上的中线分别相等,那么这两个三角形全等,
(1)小玲在思考这道题时.画出图形,写出已知和求证.
已知:在和中, , , 是边上的中线,是边上的中线, .
求证: .
请你帮她完成证明过程.
(2)小玲接着提出了两个猜想:
①如果两个三角形有两条边和第三边上的中线分别相等,那么这两个三角形全等;
②如果两个三角形有两条边和第三边上的高分别相等,那么这两个三角形全等;
请你分别判断这两个猜想是否正确,如果正确,请予以证明,如果不正确,请举出反例.

-
17、学校体育组为了解本学期九年级女生体质健康的变化情况,从九年级全体女生中随机抽取名女生进行体质测试,并调取这名女生上学期的体质测试成绩进行对比.经过对两次成绩进行整理、描述和分析,得出了下面的部分信息:
【信息1】两次测试成绩(满分为100分)的频数分布直方图如下:
(数据分组: , , , , )

【信息2】抽取的名女生上学期测试成绩在的具体分数是:
80 81 83 84 84 88
【信息3】抽取的名女生两个学期测试成绩的平均数、中位数、众数如下表:
学期
平均数
中位数
众数
上学期
82.9
84
本学期
82.9
86
86
根据以上信息,解答下列问题:
(1)本题中,的值为___________,的值为_________.
(2)学校体育组计划根据本学期统计数据安排九年级80分以下的同学参加体质加强训练项目,若九年级共有90名女生,估计参加此项目的女生人数.
(3)小林比较了两个学期测试成绩的平均数,发现没有区别,从而得出结论:九年级女生的体质健康没有发生变化.你是否同意他的看法?请说明理由.
-
18、如图,在的方格中,的顶点均在格点上.试按要求画出线段(E,F均为格点),各画出一条即可.

-
19、计算:(1) ; (2)
-
20、如图,已知正方形与正方形 , , 分别是 , 的中点,当点落在线段上时,点恰好在上.记正方形的面积为 , 正方形的面积为 , 则 .