-
1、如图1,将一条两边互相平行的纸带先沿EF折叠,再沿AF折叠得图2.设∠BEC'=x度,则∠EFD”=.度(用含x的代数式表示).
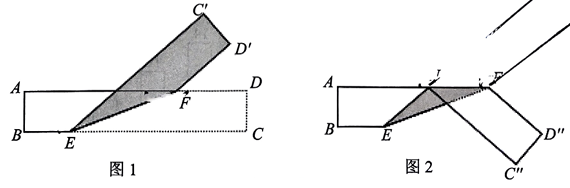
-
2、已知a-b= , ab=2,则(5-3a)(5+3b)的值为.
-
3、小刘同学购置一本《朝花夕拾》共144页,计划10天读完,当他读完一半页数时,发现平均每天要多读6页才能按时读完,设该同学读前一半页数时,平均每天读x页,根据题意列出方程.
-
4、某校100名学生参加安全知识竞赛,将得分情况分为五组,第一组到第四组的频数分别为5,8,32,35,则第五组的频率是.
-
5、要使分式有意义,则x的值可以为(写出一个即可)·
-
6、现有若干个长为a,宽为b的小长方形(如图1).将其中2个小长方形摆放在边长为a的正方形内(如图2),右下角阴影部分的面积为9;再将其中3个小长方形摆放在边长为的正方形内(如图3),记右上角的阴影部分面积为 , 右下角的阴影部分面积为.若 , 则的值为( )
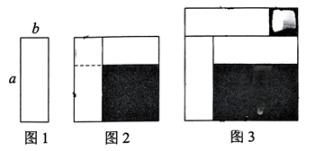 A、10 B、 C、11 D、
A、10 B、 C、11 D、 -
7、已知 , 则分式的值为( )A、5 B、 C、 D、1
-
8、《九章算术》中关于“盈不足术”的记载,其译文为:有几个人去买鸡,每人出9钱,余11钱;每人出6钱,差16钱.问人数和鸡价各多少?小温同学根据题意,列得方程组 , 则方程组中x表示的是( )A、鸡的数量 B、鸡的单价 C、每个人出的钱数 D、买鸡的人数
-
9、如图,将沿射线BC向右平移6个单位得。若 , 则BF的长是( )
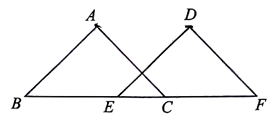 A、15 B、9 C、6 D、3
A、15 B、9 C、6 D、3 -
10、下列因式分解错误的是( )A、 B、 C、 D、
-
11、下列各组数是方程的解的是( )A、 B、 C、 D、
-
12、下列运算正确的是( )A、 B、 C、 D、
-
13、如图是2025年温州市5月1日至5日每天最高、最低气温的折线统计图,在这5天中,日温差最小的一天是( )
 A、1日 B、2日 C、4日 D、5日
A、1日 B、2日 C、4日 D、5日 -
14、2025年气候监测发现,每立方米空气中含某污染物约0.0000000305克,数据0.0000000305用科学记数法表示为( )A、3.05x10-8 B、3.05x10-7 C、0.305x10-7 D、30.5x10-9
-
15、如图,直线a,b被直线c所截,下列各角中与∠1是内错角的是( )
 A、∠2 B、∠3 C、∠4 D、∠5
A、∠2 B、∠3 C、∠4 D、∠5 -
16、如图,内接于 , 为直径,在延长线上取一点E,使得 , 连结 , 在下方,作 , 连结交于点D,连结 .
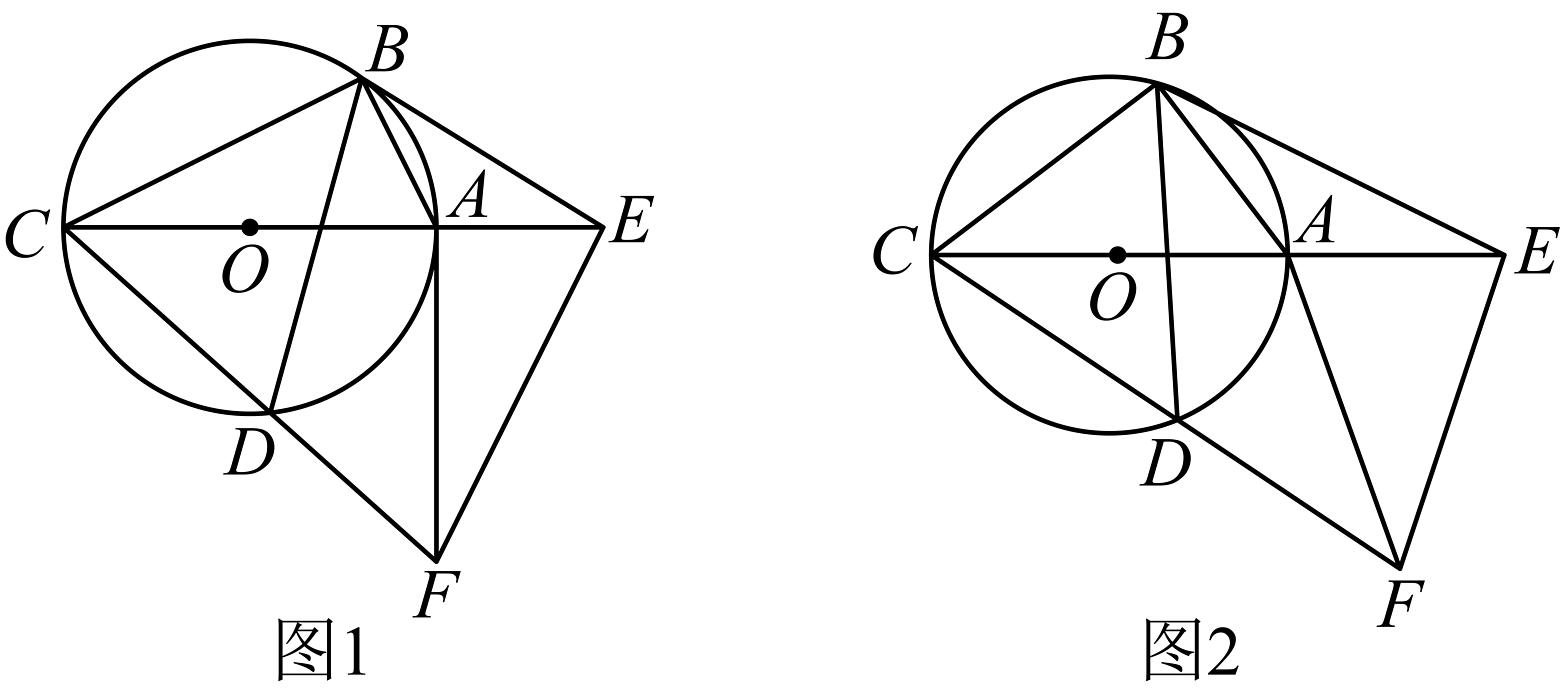 (1)、如图1,若 .
(1)、如图1,若 .①求证:;
②若 , , 求的长度;
(2)、如图2,若 , 时,求证: . -
17、已知二次函数 , 回答下列问题:(1)、若该函数图象经过点
求该函数图象与轴的交点坐标;
点向上平移个单位长度,向右平移个单位长度后,落在二次函数图象上,求的值.
(2)、若该函数图象经过点与点 , 且与轴的两个交点到点的距离均小于 , 求证: . -
18、如图,在平行四边形中,对角线与相交于点O,点E,F,G分别为 , , 的中点,连结 , , .
 (1)、求证:四边形为平行四边形;(2)、如图1,若 , 求证:;(3)、如图2,当平行四边形为菱形时,若 , , 求四边形的面积.
(1)、求证:四边形为平行四边形;(2)、如图1,若 , 求证:;(3)、如图2,当平行四边形为菱形时,若 , , 求四边形的面积. -
19、在现代智能仓储系统中,一款名为“”的智能机器狗,为了研究其载重能力W(千克)与其运动速度v(米/秒)的关系,工程师通过实验测得以下数据:
载重W(kg)
…
10
12
15
20
30
…
速度v(m/s)
…
6
5
4
3
2
…
 (1)、把表中W,v的各组对应值作为点的坐标,如 , …,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;(2)、观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;(3)、某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量.
(1)、把表中W,v的各组对应值作为点的坐标,如 , …,已在图中坐标系描出了相应的点,请用平滑的曲线顺次连接这些点;(2)、观察所画的图象,猜测v与W之间的函数关系,并求出函数关系式;(3)、某次任务要求机器狗在8分钟内将货物运送至2400米外的分区货架,求此时机器狗能承载的最大货物重量. -
20、如图,小明利用无人机测大楼的高度 . 在空中点测得:到地面上一点处的俯角 , 距离米,到楼顶点处的俯角 . 已知点与大楼的距离为70米.(点共线且图中所有的点都在同一平面内)
 (1)、求点到地面的距离;(2)、求大楼的高度 . (结果保留根号)
(1)、求点到地面的距离;(2)、求大楼的高度 . (结果保留根号)