-
1、 如图①,平面内有一点P到的三个顶点的距离分别为FA、PB、PC,若有 , 则称点P为关于点C的勾股点.
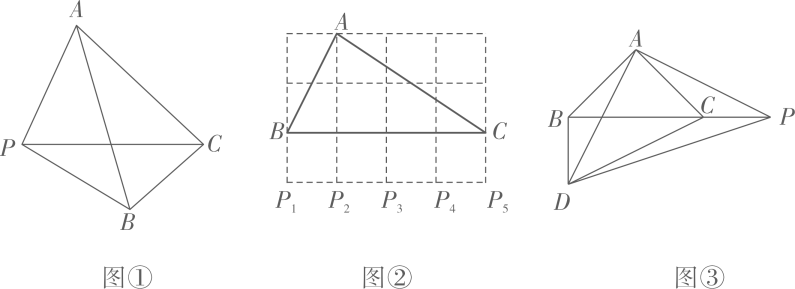 (1)、 如图②,在的方格纸中,每个小正方形的边长均为1,的顶点在格点上,则 , , , , 这五个点中是关于点A的勾股点的有 (填“ , , , , ”);(2)、 如图③,为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角(点A、P、D顺时针排列), , 连接DC,DB,求证:点P为关于点D的勾股点.
(1)、 如图②,在的方格纸中,每个小正方形的边长均为1,的顶点在格点上,则 , , , , 这五个点中是关于点A的勾股点的有 (填“ , , , , ”);(2)、 如图③,为等腰直角三角形,P是斜边BC延长线上一点,连接AP,以AP为直角边作等腰直角(点A、P、D顺时针排列), , 连接DC,DB,求证:点P为关于点D的勾股点. -
2、 为了解某校八年级学生每周参加课外阅读的时间(单位:h),随机调查了该校八年级a名学生,根据统计的结果,绘制出如下的统计图①和图②.
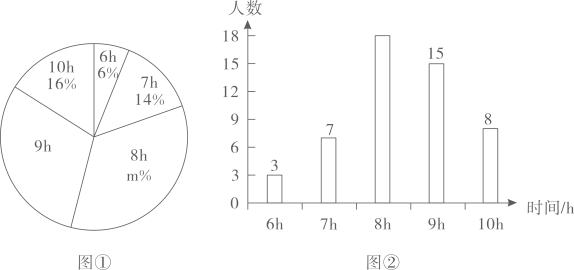
请根据相关信息,解答下列问题:
(1)、填空:a的值为 , 图①中m的值为 , 统计的这组学生每周参加课外阅读的时间数据的众数和中位数分别为和;(2)、求统计的这组学生每周参加课外阅读的时间数据的平均数;(3)、根据样本数据,若该校八年级共有学生500人,估计该校八年级学生每周参加课外阅读的时间不低于9h的人数约为多少? -
3、 如图,已知菱形ABCD的对角线交于点O,E、F是对角线BD所在直线上的两点,且 , DF=BE,连接AE、CE、AF、CF,得四边形AECF. 求证:四边形AECF是正方形.

-
4、 如图,直线与交于点A.
 (1)、 求点A的坐标;(2)、 根据图象,直接写出的解集.
(1)、 求点A的坐标;(2)、 根据图象,直接写出的解集. -
5、 如图,在平面直角坐标系中,点 , , , 都在 x 轴上,点 , , , 都在直线 上, , 且 , , , , , 分别是以 , , , , , 为直角顶点的等腰直角三角形,则 的面积是.
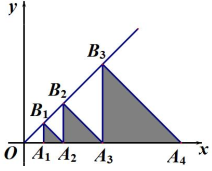
-
6、 如图,长方形内有两个相邻的正方形,其面积分别为18和50,则图中阴影部分的面积为.

-
7、 已知直角三角形的两直角边的长分别是6和8,则斜边上的中线长为.
-
8、 珠海市举办了“传诵经典”青少年演讲比赛,其中综合荣誉分占 , 现场演讲分占 , 小明参加并在这两项中分别取得80分(综合荣誉)和90分(现场演讲)的成绩,则小明的最终成绩为.
-
9、 如图,平行四边形ABCD的对角线AC,BD相交于点O,AE平分 , 分别交BC、BD于点E、P,连接OE, , , 则下列结论错误的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
10、“漏刻”是我国古代一种利用水流计时的工具(如图①),综合实践小组用甲、乙两个透明的竖直放置的容器和一根装有节流阀(控制水的流速)的软管,制作了类似“漏刻”的简易计时装置(如图②).上午10:00,综合实践小组在甲容器里加满水,经过实验得到甲容器的水面高度h(cm)与流水时间t(min)的关系如图③所示,下列说法错误的是( )
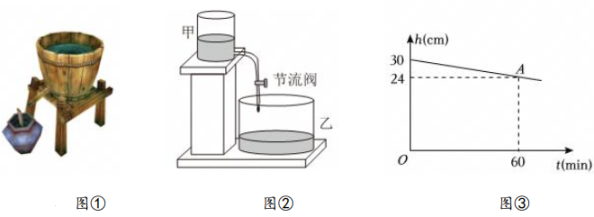 A、甲容器的初始水面高度为30cm B、15:00甲容器的水流光 C、甲容器的水面高度h与流水时间t的关系式为 D、12:00时甲容器的水面高度为12cm
A、甲容器的初始水面高度为30cm B、15:00甲容器的水流光 C、甲容器的水面高度h与流水时间t的关系式为 D、12:00时甲容器的水面高度为12cm -
11、 如图, 在 中, , , , GA在数轴上, 以点 A 为圆心, AB 的长为半径画弧, 交数轴于点 P ,则点 P 表示的数是( )
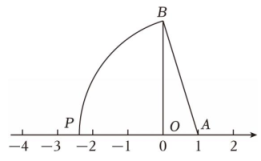 A、 B、 C、 D、
A、 B、 C、 D、 -
12、 下列命题的逆命题正确的是( )A、全等三角形的面积相等 B、全等三角形的周长相等 C、两个锐角互余的三角形是直角三角形 D、如果 , 那么
-
13、 如图,小华注意到跷跷板静止状态时,可以与地面构成一个 , 跷跷板中间的支撑杆EF垂直于地面(E、F分别为AB、AC的中点),若 , 则点B距离地面的高度为( )
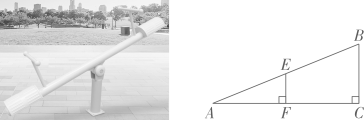 A、80cm B、70cm C、60cm D、50cm
A、80cm B、70cm C、60cm D、50cm -
14、 为了解甲、乙两种甜玉米产量的情况,农科院各用10块自然条件相同的试验田进行试验,得到的各试验田每公顷的产量绘制统计图如图,下列判断正确的是( )
 A、甲种甜玉米产量稳定 B、乙种甜玉米产量稳定 C、两种甜玉米的产量一样稳定 D、无法确定哪一种品种的产量更稳定
A、甲种甜玉米产量稳定 B、乙种甜玉米产量稳定 C、两种甜玉米的产量一样稳定 D、无法确定哪一种品种的产量更稳定 -
15、 二次根式中字母x的取值范围是( )A、 B、 C、 D、
-
16、 把直线 向上平移 3 个单位长度得到的直线为( )A、 B、 C、 D、
-
17、 下列式子是最简二次根式的是( )A、 B、 C、 D、
-
18、如图,在平面直角坐标系中,点A(a,0),B(m,b),且
+|b-5|=0,m是64的立方根.
 (1)、直接写出:a= , b= , m=;(2)、将线段AB平移得到线段CD,点B的对应点是点C(8,0),点A的对应点是点D.
(1)、直接写出:a= , b= , m=;(2)、将线段AB平移得到线段CD,点B的对应点是点C(8,0),点A的对应点是点D.①在平面直角坐标系中画出平移后的线段CD,直接写出点D的坐标;
②若点M在y轴上,且三角形ACM的面积是6,求点M的坐标;
(3)、在(2)的条件下,点E在y轴负半轴上运动,但不与点D重合,直接写出∠BEC、∠ABE、∠DCE之间的数量关系. -
19、某校组织师生参加夏令营活动,现准备租用A、B两种型号客车(每种型号的客车至少租用一辆),A型车每辆租金500元,B型车每辆租金600元.若5辆A型车和2辆B型车坐满后共载客310人;3辆A型车和4辆B型车坐滴后共载客340人.
 (1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两种型号客车外,又派出甲、乙两辆器材运输车,已知从学校到目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地,如图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲车关于s与t的函数解析式.
(1)、每辆A型车、B型车坐满后各载客多少人?(2)、若该校计划租用A型和B型两种客车共10辆,总租金不高于5500元,并将全校420人载至目的地.该校有几种租车方案?哪种租车方案最省钱?(3)、在这次活动中,学校除租用A、B两种型号客车外,又派出甲、乙两辆器材运输车,已知从学校到目的地的路程为300千米,甲车从学校出发0.5小时后,乙车才从学校出发,却比甲车早0.5小时到达目的地,如图是两车离开学校的路程s(千米)与甲车行驶的时间t(小时)之间的函数图象.根据图象信息,求甲车关于s与t的函数解析式. -
20、如图1,MN∥PQ,点A,B分别在直线MN,PQ上,∠ACB=90°,∠ABQ<90°.
 (1)、若∠NAC=40°,则∠CBQ=°.(2)、若AC平分∠NAB,点R在线段AB上,连接CR.
(1)、若∠NAC=40°,则∠CBQ=°.(2)、若AC平分∠NAB,点R在线段AB上,连接CR.①如图2,当∠ACR=∠CBQ时,证明:CR⊥AB;
②如图3,延长CR交MN于点D,过点D作DF⊥AB分别交AB,PQ于点E,F,当∠DFB=2∠ADC时,证明:∠ACD=45°.