-
1、 “两条平行线被第三条直线所截”是平行线中的一个重要的“基本图形”，所有与平行线有关的角都存在于这个“基本图形”中，且都分布在“第三条直线”的两旁，当发现题目的图形“不完整”时，要通过适当的辅助线将其补完整. 将“非基本图形”转化为“基本图形”. 在“相交线与平行线”的学习中，有这样一道典型问题：
如图①，已知 ， 若 ， ， 则的度数是 ▲ .
分析：从图形上看，由于没有一条直线截AB与CD，所以无法直接运用平行线的相关性质，这就需要构造出“两条平行线被第三条直线所截”基本图形后，才可以运用平行线的条件或性质. 过E点作 ， 根据平行于第三条直线的两直线平行，可得 ， 这样可将图形转化，进而可以求出.
[方法应用]
已知.
(1)、 如图②，若 ， ， 则度；(2)、 如图②，写出、、之间的数量关系，并证明；(3)、 如图③，BE平分 ， CE平分 ， ， 求的度数. -
2、 如图1，以直角的直角顶点O为原点，以OC，OA所在直线为x轴和y轴建立平面直角坐标系，点A(0，a)，C(b，0)，并且满足.
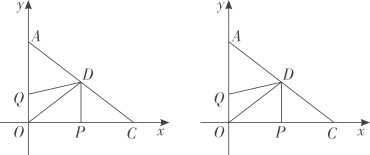(1)、 a与b的值分别是：a=；b=.(2)、 如图1，坐标轴上有两动点P，Q同时出发，点P从点C出发沿x轴负方向以每秒2个单位长度的速度匀速运动，点Q从点O出发沿y轴正方向以每秒1个单位长度的速度匀速运动，当点P到达点O整个运动随之结束；线段AC的中点D的坐标是D(4，3)，设运动时间为t秒. 是否存在 t，使得与的面积相等？若存在，求出t的值；若不存在，说明理由. -
3、 解不等式组： ， 并把解集在数轴上表示出来.
-
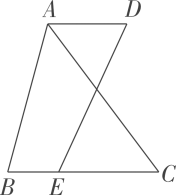
4、 如图，已知 ， AC平分 ， 若 ， 求的度数.
-
5、 如图，小正方形的边长为 1，已知鹰嘴崖坐标为 (2，1)，先建立平面直角坐标系，再写出各景点的坐标.
-
6、 解二元一次方程组：
-
7、 如图，八块相同的长方形地砖拼成一个矩形，则每块长方形地砖的面积是.
-
8、 语句“x与y的和是非负数”用不等式表示为：.
-
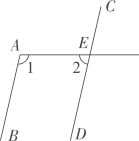
9、 如图，平行线AB，CD被直线AE所截.若 ， 则的度数为.
-
10、 将一张长方形纸条按如图所示折叠，若 ， 则的度数是（ ）
A、 B、 C、 D、 -
11、 若 ， 则下列不等式中成立的有（ ）A、 B、 C、 D、
-
12、 下列各数中没有平方根的是（ ）A、 B、 C、0 D、0.03
-
13、 不等式 的解集在数轴上表示正确的是 （ ）.A、
B、
C、
D、
-
14、 既是方程的解，又是方程的解是（ ）A、 B、 C、 D、
-
15、 与无理数最接近的整数是（ ）A、4 B、5 C、6 D、7
-
16、 如图，小手盖住的点的坐标可能是（ ）
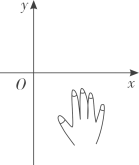A、(-3，-3) B、(2，3) C、(2，-5) D、(-3，4) -
17、 下列四个数中，最大的数是（ ）.A、3 B、-1 C、0 D、
-
18、 如图①，将矩形 GABC 放在直角坐标系中，O 为原点，点 C 在 x 轴上，点 A 在 y 轴上，GA、OC 的长 a、c 满足 ， 把矩形 GABC 沿对角线 OB 所在直线翻折，点 C落到点 D 处，OD 交 AB 于点 E.
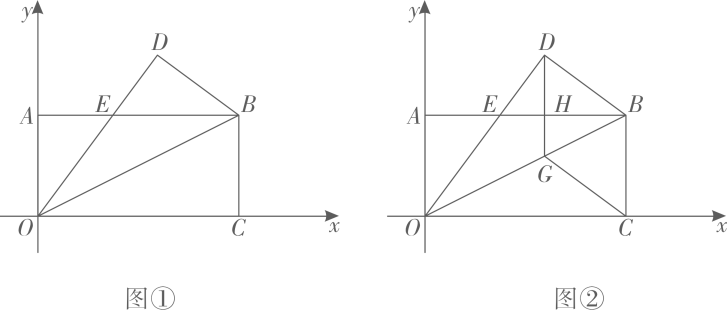(1)、 a= ， c=；(2)、 如图②，过点 D 作DG//BC，交 OB 于点 G，交 AB 于点 H，连接 CG，判断四边形 BCGD 的形状，并说明理由；(3)、 在(2)的条件下，点 M 为坐标轴上一点，直线 OB 上是否存在一点 N，使以 O、D、M、N 为顶点的四边形是平行四边形？若存在，请求出点 N 坐标；若不存在，请说明理由. -
19、综合实践：
主题
关于如何扭转汽车客运线路亏损的问题
问题情境
随着轨道交通的便利，私家车的普及，网约车的流行，某汽车客运公司的乘客量比以往减少，近期有一条运营线路处于亏损运营状态.
问题探究
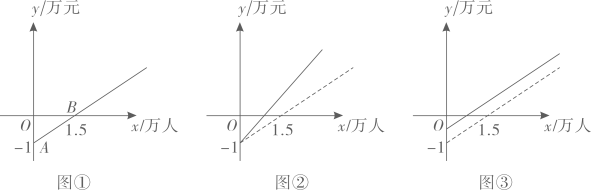
⑴公司做了大量的市场调研，将有关数据进行分析整理，发现收支差额y（万元）（票价总收入减去运营成本）与乘客数量x（万人）的关系可近似看作一次函数（图象如图① 所示），写出图①中点A（0，-1）和点B（1.5，0）的实际意义，并求出y与x的函数关系.
⑵汽车客运公司在调研后邀请了一些乘客代表来研讨亏方案，在讨论中，有乘客代 表认为，市民出行选择方式增多，客运公司应该改变观念，改善管理，降低运营成本， 客运公司行政代表认为，运营成本难以下降，提高票价才能亏，你认为图②和图③两个图示中，反映乘客代表意见的是▲ ， 反映客运公司行政代表意 见的是▲.（填序号） |
问题解决
⑶汽车客运公司通过市场调研，发现该线路一周内平均每天的乘客数量为1.2万人， 经过讨论，得到三种亏方案，具体如下：
方案1：票价不变，将运营成本降低到0.7万元；
方案2：运营成本不变，提高票价使每万人收入差额提高到0.9万元；
方案3：将运营成本降低到0.85万元，同时提高票价，使每万人收入差额提高到0.75万 元，你认为哪种方案更有利于汽车客运公司招转亏损？请说明理由.
-
20、 如图，做如下操作：对折矩形 ABCD，使 AD 与 BC 重合，得到折痕 EF，把纸片展平；再一次折叠纸片，使点 A 落在 EF 上的点 P 处，得到折痕 BM，BM 与 EF 交于点 N，若直线 BP 交直线 CD 于点 Q.
(1)、 猜想 的度数，并说明理由；(2)、 若 ， ， 求线段 QD 的长.