相关试卷

1、如图所示，点 P，Q分别是等边三角形ABC 边AB，BC上的动点（端点除外），点P，点Q 以相同的速度，同时从点 A，点B 出发.

(1)、如图甲，连结AQ，CP.求证：△ABQ≌△CAP.

(2)、如图甲，当点 P，Q分别在AB，BC边上运动时，AQ，CP 相交于点M，∠QMC 的大小是否变化?若变化，请说明理由；若不变，求出它的度数.

(3)、如图乙，当点 P，Q在AB，BC 的延长线上运动时，直线AQ，CP 相交于M，∠QMC 的大小是否变化?若变化，请说明理由；若不变，求出它的度数.

查看解析
2、如图所示，在△ABC 中，∠ABC=40°，∠ACB=90°，AE 平分. $∠ B A C$ 交BC 于点E. P 是边BC上的动点（不与B，C 重合），连结AP，将△APC 沿AP 翻折得△APD，连结 DC，记∠BCD=α.

(1)、当 P 与E 重合时，求α的度数.

(2)、当 P 与E 不重合时，记∠BAD=β，请探究α与β的数量关系.

查看解析
3、如图所示，在△ABC 中，∠ACB=90°，AC=BC，若点C 的坐标为（-1，0），点 A 的坐标为（-4，2），则点 B 的坐标为.

查看解析
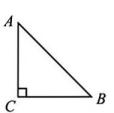
4、如图所示，∠EOF 的顶点O 是边长为2的等边三角形ABC的重心， $∠ E O F$ 的两边与 $△ A B C$ 的边交于E，F，∠EOF=120°，则∠EOF 与 $△ A B C$ 的边所围的阴影部分的面积是.

查看解析
5、如图所示，O 是△ABC 的三条角平分线的交点，连结OA，OB，OC，若△OAB，△OBC，△OAC 的面积分别为S₁ ， S₂ ， S₃ ，则下列关系中，正确的是（）

A、 $S_{1} > S_{2} + S_{3}$ B、 $S_{1} = S_{2} + S_{3}$ C、 $S_{1} < S_{2} + S_{3}$ D、无法确定

查看解析
6、如图所示，AC平分∠BCD，AB=AD，AE⊥BC于点E，AF⊥CD于点F.

(1)、若∠ABE=60°，求∠CDA 的度数.

(2)、若AE=2，BE=1，CD=4.求四边形ABCD 的面积.

查看解析
7、在△ABC中，∠A=50°，∠B=30°，点 D 在AB 边上，连结CD，若△ACD为直角三角形，则∠BCD 的度数为度.

查看解析
8、已知三角形两边的长分别是3 和6，第三边的长是方程 $x^{2} - 6 x + 8 = 0$ 的根，则这个三角形的周长等于.

查看解析
9、如图所示的网格是由边长相同的小正方形组成，点A，B，C，D，E，F，G在小正方形的顶点上，则△ABC 的重心是（）

A、点D B、点E C、点F D、点G

查看解析
10、如图所示，在四边形ABCD 中，P 是对角线BD 的中点，E，F 分别是AB，CD 的中点，AD=BC，∠PEF=30°，则∠PFE 的度数是（）

A、15° B、20° C、25° D、30°

查看解析
11、用反证法证明命题“在直角三角形中，至少有一个锐角不大于45°”时，应假设直角三角形中（）

A、两锐角都大于 45° B、有一个锐角小于45° C、有一个锐角大于45° D、两锐角都小于 45°

查看解析
12、如图所示，CD⊥AB 于点D，已知∠ABC 是钝角，则（）

A、线段CD 是△ABC 的AC 边上的高线 B、线段CD 是△ABC 的AB 边上的高线 C、线段AD 是△ABC 的BC 边上的高线 D、线段AD 是△ABC 的AC 边上的高线

查看解析
13、车间里有五台车床同时出现故障，已知第一台至第五台修复的时间如下表：
车床代号
A
B
C
D
E
修复时间/分
15
8
29
7
10
已知每台车床停产一分钟造成经济损失 10元，修复后即可投入生产.
Ⅰ.若只有一名修理工，且每次只能修理一台车床，则下列三个修复车床的顺序：①D→B→E→A→C；②D→A→C→E→B；③C→A→E→B→D中，经济损失最少的是(填序号).
Ⅱ.若由两名修理工同时修理车床，且每台车床只由一名修理工修理，则最少经济损失为元.

查看解析
14、1202年数学家斐波那契在《计算之书》中记载了一列数：1，1，2，3，5，…，这一列数满足：从第三个数开始，每一个数都等于它前面两个数之和，则在这一列数的前2024个数中，奇数的个数为( )

A、676 B、674 C、1348 D、1350

查看解析
15、琪琪准备完成题目：计算： $(- 9) \times (\frac{1}{2} -) - 3^{3} .$ 发现题中有一个数字“■”被墨水污染了.

(1)、琪琪猜测被污染的数字“■”是 $\frac{2}{3}$ ，请计算： $(- 9) \times (\frac{1}{2} - \frac{2}{3}) - 3^{3};$

(2)、琪琪的妈妈看到该题标准答案的结果等于-9，请通过计算求出被污染的数字“■”.

查看解析
16、如图，一只蚂蚁从点 A 出发沿数轴向右爬行2个单位长度到达点 B，点A 所表示的数为 $- \sqrt{2} .$ 设点 B 所表示的数为m，则|m-3|+m+2的值为.

查看解析
17、有一列数，记第n个数为 $a_{n}$ ，已知 $a_{1} = 2,$ 当n>1时 $a_{n} = \{\begin{matrix} \frac{1}{a_{n - 1}} (n 为偶数), \\ \frac{1}{1 - a_{n - 1}} (n 为奇数), \end{matrix}$ 则 $a_{2025}$ 的值为.

查看解析
18、定义新运算：①在平面直角坐标系中，{a，b}表示动点从原点出发，沿着x轴正方向(a≥0)或负方向(a<0)平移|a|个单位长度，再沿着y轴正方向(b≥0)或负方向(b<0)平移|b|个单位长度.例如，动点从原点出发，沿着x轴负方向平移2个单位长度，再沿着 y轴正方向平移1个单位长度，记作{-2，1}.②加法运算法则：{a，b}+{c，d}={a+c，b+d}，其中a，b，c，d为实数.若{3，5}+{m，n}={-1，2}，则下列结论正确的是( )

A、m=2，n=7 B、m=-4，n=-3 C、m=4，n=3 D、m=-4，n=3

查看解析
19、计算：

(1)、 $∣ - 4 ∣ + {(- 2)}^{0} - \sqrt{9};$

(2)、 ${(π - 5)}^{0} + \sqrt{8} - 2 s i n 3 0^{\circ} +$ $∣ - \sqrt{2} ∣;$

(3)、 $- 2 \cdot c o s 4 5^{\circ} + {(π - 3.14)}^{0} +$ $|1 - \sqrt{2}| + {(\frac{1}{4})}^{- 1} .$

查看解析
20、下列算式中，结果与有理数 $- 2 \frac{2}{3}$ 相等的是( )

A、 $(- 2) \times \frac{2}{3}$ B、 $- (2 \times \frac{2}{3})$ C、 $- 2 + \frac{2}{3}$ D、 $- 2 - \frac{2}{3}$

查看解析

上一页 467 468 469 470 471 下一页跳转

车床代号	A	B	C	D	E
修复时间/分	15	8	29	7	10