相关试卷
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.3多项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.2单项式的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.1同底数幂的乘法 同步练习---提高篇
- 2017-2018学年数学浙教版七年级下册3.7整式的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.6同底数幂的除法 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.5整式的化简 同步练习---基础篇
- 2017-2018学年数学浙教版七年级下册3.4乘法公式 同步练习---基础篇
-
1、某校八年级组织了一场趣味运动会,其中“背夹球竞走”项目的规则是:每组选出男、女同学各一名,背靠背中间夹一个气球,在直道上侧身走完规定的路程,气球不能落地。若途中气球掉落,须捡回并在掉落处继续前行。用时少者胜。甲、乙两组参加比赛,结果甲组在途中掉了球,乙组则顺利走完全程。
图反映了比赛过程中,两组同学距离出发点的距离y(m)与比赛时间x(s)的函数关系。
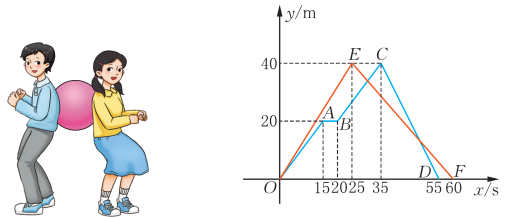
根据函数图象,回答下列问题:
(1)、这项比赛的总路程是多少?(2)、哪一组同学获胜?(3)、线段AB表示的实际意义是什么?(4)、比赛途中两组同学相遇了几次?在哪个时间段内他们第一次相遇? -
2、根据卫生要求,游泳池必须定期换水、清洗。某游泳池在上午9:00打开排水口开始排水,排水口的排水速度保持不变,其间因清洗游泳池需要暂停排水,游泳池的水在12:00全部排完。游泳池内的水量Q(m3)是排水时间t的函数,函数图象如图所示。根据图象回答下列问题。
 (1)、开始排水前,游泳池内的水量有多少?(2)、几时该游泳池开始暂停排水进行清洗?暂停排水时间有多长?(3)、排水口的排水速度是多少?暂停排水时游泳池内还剩多少水量?
(1)、开始排水前,游泳池内的水量有多少?(2)、几时该游泳池开始暂停排水进行清洗?暂停排水时间有多长?(3)、排水口的排水速度是多少?暂停排水时游泳池内还剩多少水量? -
3、如图,是等边三角形. , 是边上的高,点E在边上,连接 , 以为边在其下方作等边 , 连接 .
 (1)、当是等腰三角形时, ;(2)、求证:;(3)、当是等腰三角形时,求的大小;(4)、直接写出的最小值.
(1)、当是等腰三角形时, ;(2)、求证:;(3)、当是等腰三角形时,求的大小;(4)、直接写出的最小值. -
4、如图,在中, , , 是的垂直平分线,交于点E,交于点D.
 (1)、求的度数:(2)、如图2,若于点F,连接交于点H.
(1)、求的度数:(2)、如图2,若于点F,连接交于点H.①求证:垂直平分;
②若 , , 且 , 求的长(用含m,n的式子表示).
-
5、如图,在和中, , .
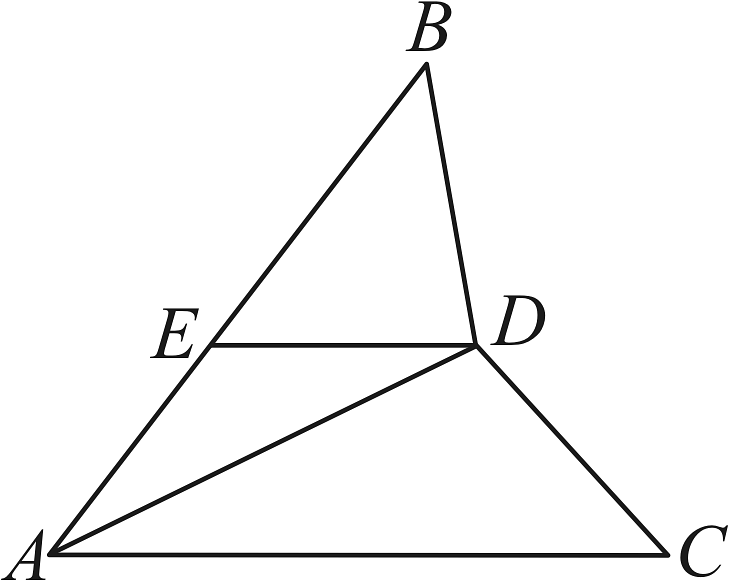 (1)、求证:;(2)、过点D作交于点E,求证:是等腰三角形.
(1)、求证:;(2)、过点D作交于点E,求证:是等腰三角形. -
6、如图,小明在游乐场玩两层型滑梯,每层楼梯高度相同(),都为2.5米,他想知道左右两个滑梯和的长度是否相等,于是制定了如下方案:

课题
探究两个滑梯的长度是否相等
测量工具
长度为6米的卷尺
测量步骤
①测量线段的长度;②测量线段的长度
测量数据
米,米
(1)、根据小明的测量方案和数据,判断两个滑梯和的长度是否相等?并说明理由;(2)、猜想两个滑梯和所在直线的位置关系,并证明. -
7、如图,在的方格图中,每个小方格都是边长为1个单位的正方形,每个小正方形的顶点叫做格点.已知的三个顶点在格点上.
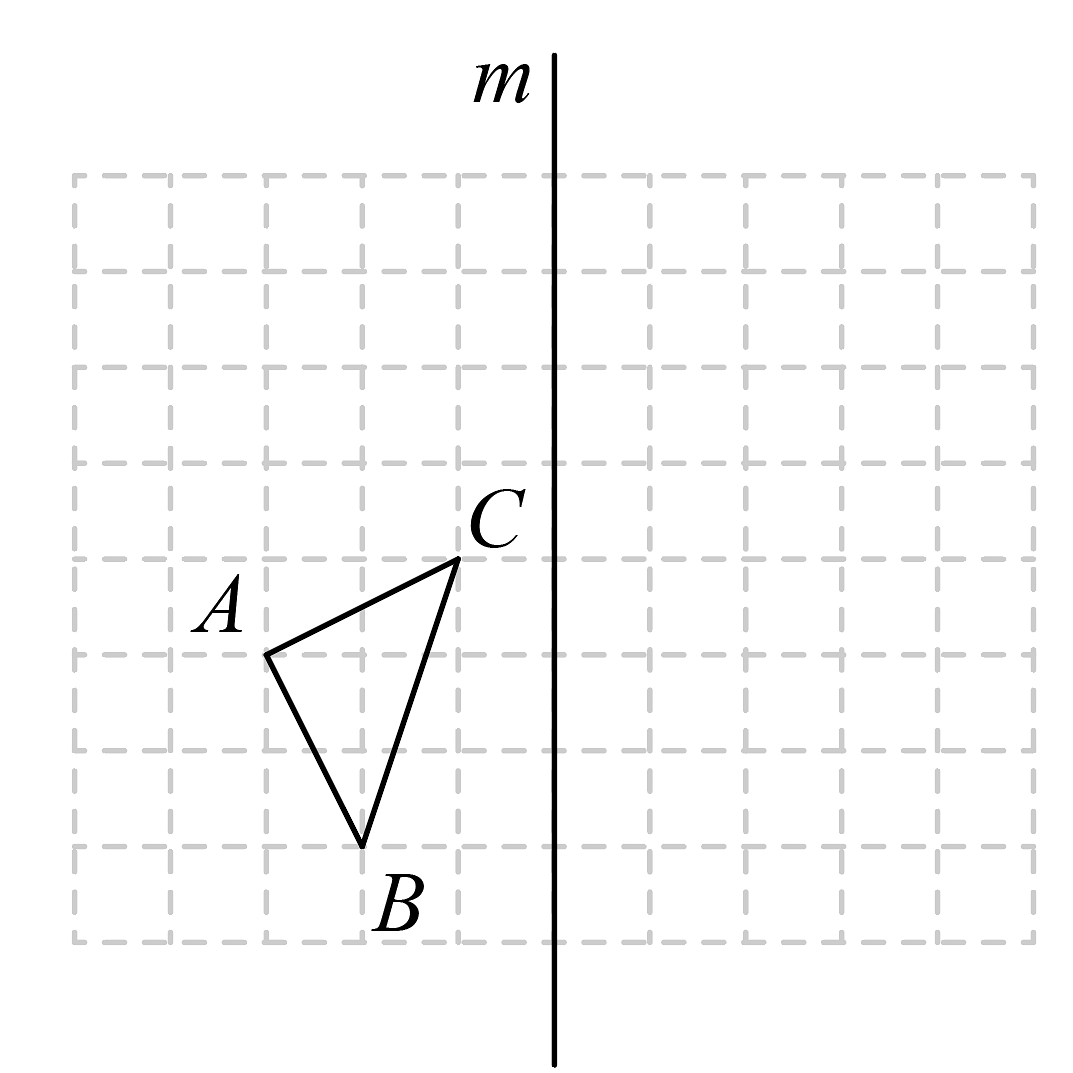 (1)、画出 , 使它与关于直线m对称;(2)、在直线m上找一点D,使得的和最小:(保留作图痕迹)(3)、延长交直线m于E,若是以为底边的等腰三角形,那么图中这样的格点F共有 个.
(1)、画出 , 使它与关于直线m对称;(2)、在直线m上找一点D,使得的和最小:(保留作图痕迹)(3)、延长交直线m于E,若是以为底边的等腰三角形,那么图中这样的格点F共有 个. -
8、如图是等边三角形,是中线,延长到 , 使 . 求证: .

-
9、如图,在中, , 面积是14,的垂直平分线分别交边于E、F点.若点D为边的中点,点M为线段上一动点,则的最小值为

-
10、在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图方法进行测量,其中 , , 测得 , , 则圆形容器的壁厚是cm.

-
11、如图,是的边的垂直平分线,D为垂足,交于点E,且 , , 求的周长.
-
12、等腰三角形的一个角为 , 则它另外两个角的度数为 .
-
13、如图,E、F分别是等边三角形的边 , 上的点,且 , , 交于点P.
 (1)、求证:;(2)、求的度数.
(1)、求证:;(2)、求的度数. -
14、如图,和分别在线段的两侧,点 , 在线段上, , , , 求证: .

-
15、(1)先化简,再求值: , 且的值满足 .
(2) .
-
16、如图所示,在中, , 厘米,厘米,点D为的中点.如果点P在线段上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段上由C点向A点运动,当点Q的运动速度为厘米/秒时,能够在某一时刻使与全等.

-
17、已知 , 则 .
-
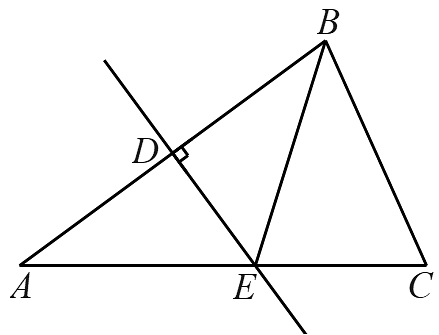
18、如图,在中,于点D,于点E.若点P是上一动点,连接 , 则的最小值是等于下列哪条线段的长( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、如图,在中, , 边的垂直平分线交于点D,交于点E,连接 , 将分成两个角,且 , 则的度数是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
20、有理数 , 表示在数轴上得到点 , , 我们就把 , 叫做 , 的一维坐标,一般的称为点与点之间的距离.如表示与之差的绝对值,实际上也可以理解为与两数在数轴上所对应的两点之间的距离.(1)、______;数轴上与两数所对应的两点之间的距离表示为____________(2)、试用数轴探究:当时,的值是____________(3)、找出所有符合条件的整数 , 使得 , 这样的整数有__________.(直接写出答案)(4)、利用数轴求出的最小值.(直接写出答案即可)