相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
1、电影《哪吒之魔童闹海》于北京时间年月日全球累计票房(含预售及海外)突破亿元.数据亿用科学记数法表示为( )A、 B、 C、 D、
-
2、我们定义:有两条边相等,一组对角互补的四边形称为“奇妙”四边形,其中相等的这组边称为“奇妙”边.(1)、下列选项中一定是“奇妙”四边形的是______.(填写序号);
①平行四边形 ②矩形 ③菱形 ④正方形
(2)、如图,在四边形中,平分 , 请说明四边形是“奇妙”四边形;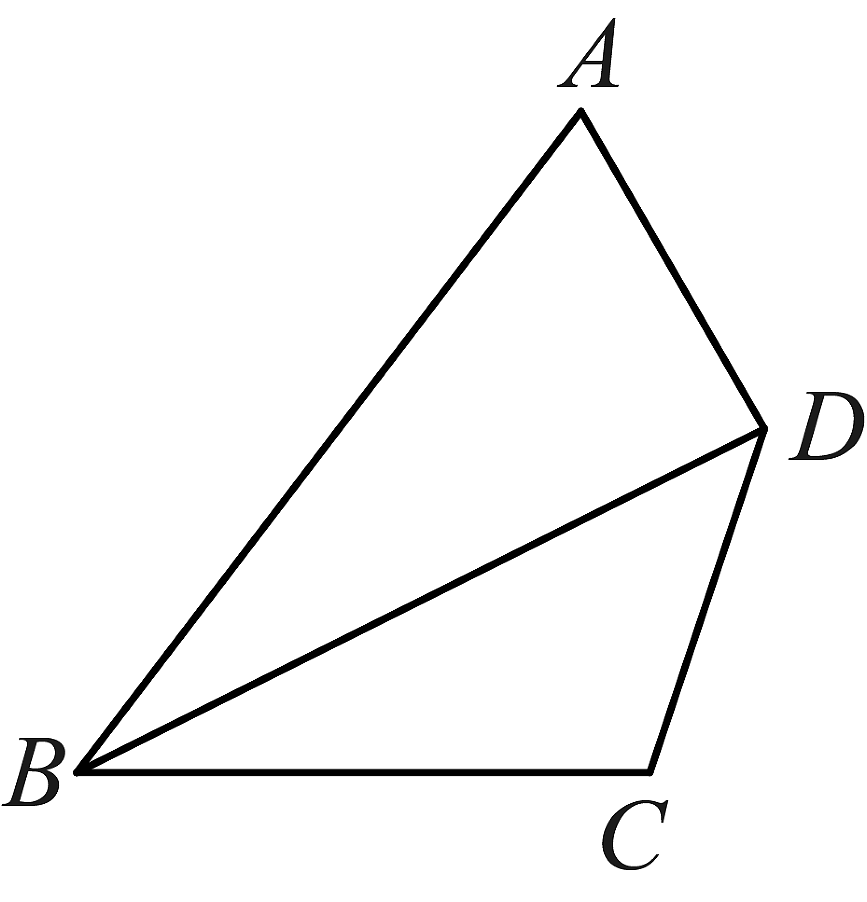 (3)、已知在“奇妙”四边形中,“奇妙”边为两相邻边,其中一条“奇妙”边 , 对角线 , 求该“奇妙”四边形的周长.
(3)、已知在“奇妙”四边形中,“奇妙”边为两相邻边,其中一条“奇妙”边 , 对角线 , 求该“奇妙”四边形的周长. -
3、综合与实践
活动主题
扇面制作
活动情景
如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市2025年传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2所示,扇面形状为扇环,已知 , , .
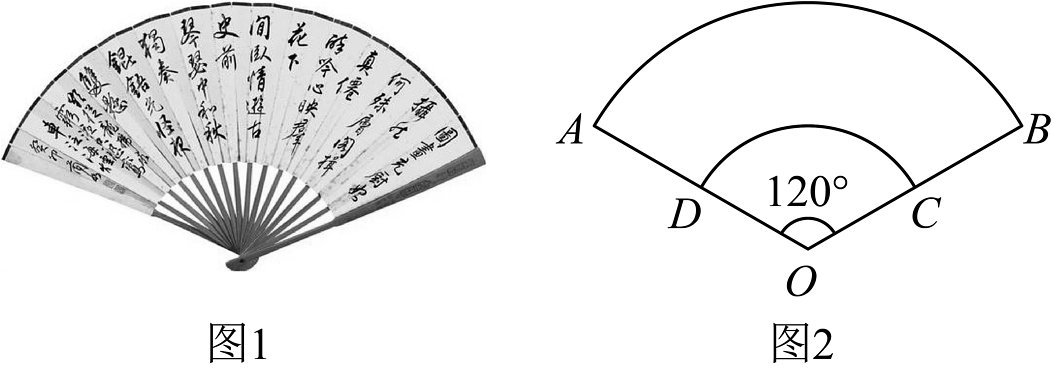
活动小组
甲组
乙组
制作工具
直尺、三角板、量角器、圆规、剪刀
制作材料
【任务一】确定弦的长度.
如图2,请你求出 所对弦的长度.
【任务二】设计甲组扇面.
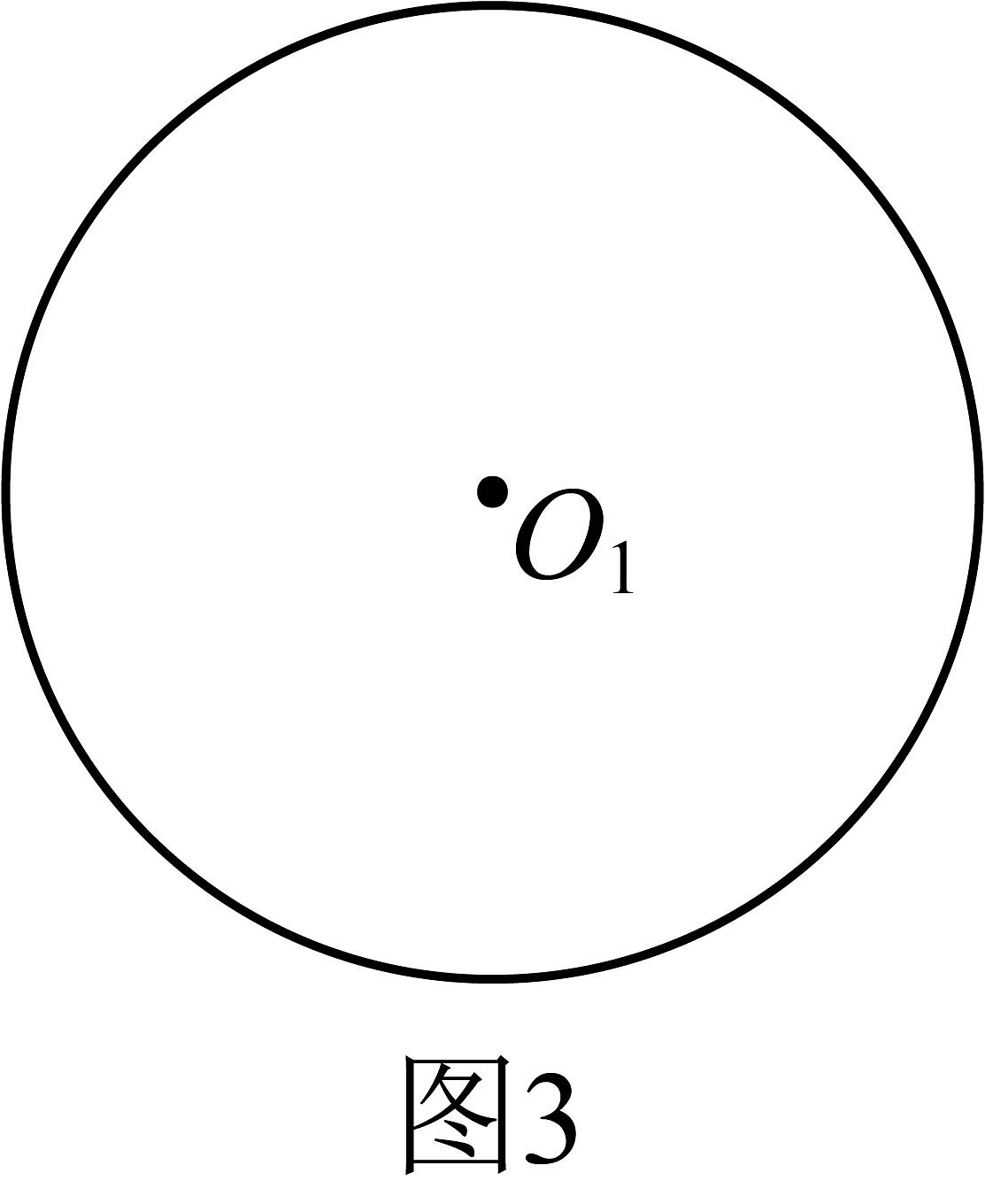
如图3,已知甲组的圆形卡纸直径为请运用表格中所给工具在中设计与图2相同的扇面,并标出相应数据.
【任务三】确定卡纸大小.
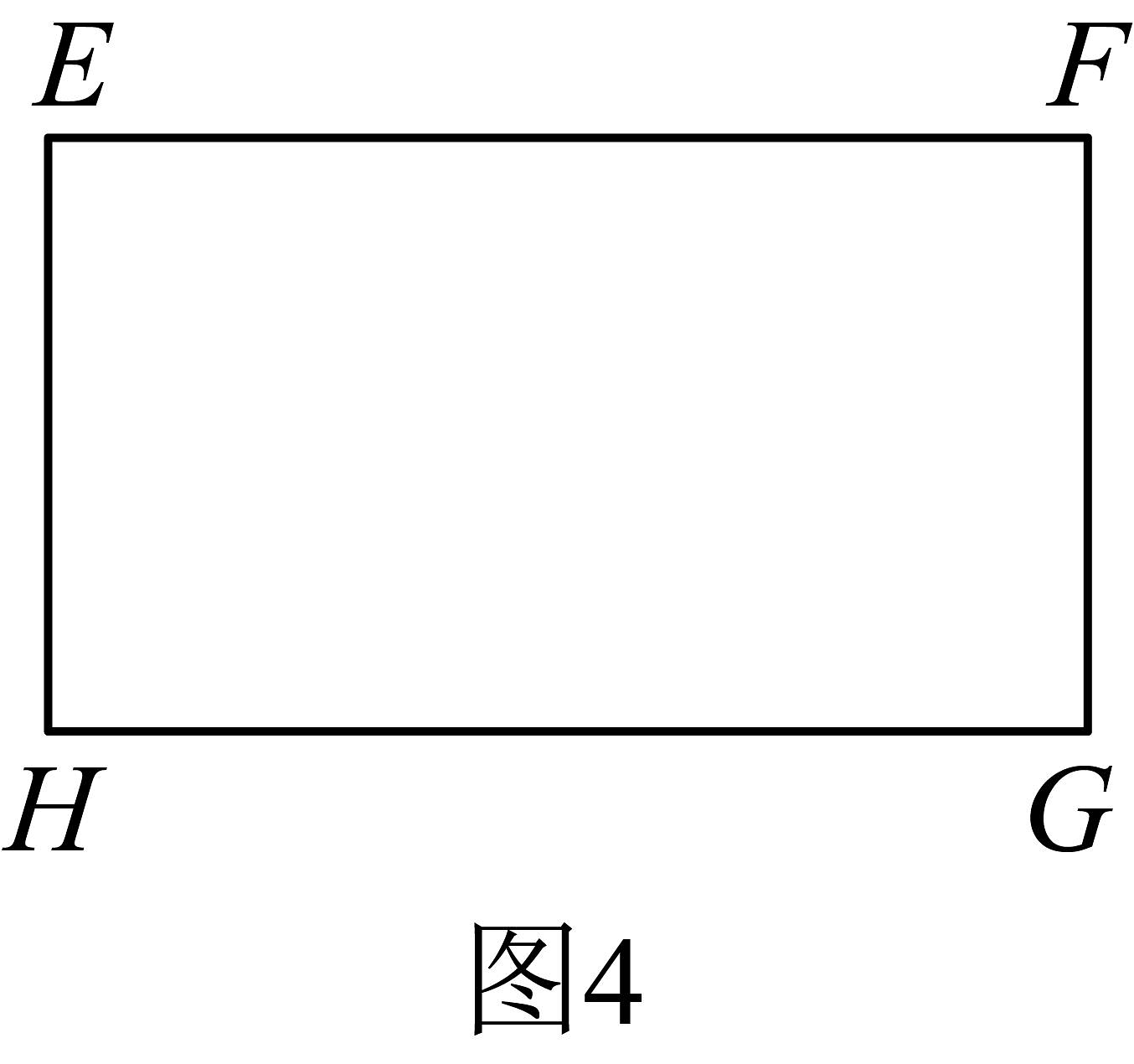
如图4,乙组利用矩形卡纸 , 恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
-
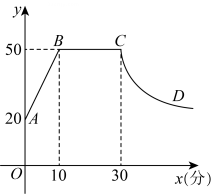
4、心理学研究发现,一般情况下,在一节45分钟的课中,学生的注意力随学习时间的变化而变化.开始学习时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的稳定状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力指标数y随时间x(分钟)的变化规律如下图所示(其中、分别为线段,为双曲线的一部分).
(1)开始学习后第5分钟时与第35分钟时相比较,何时学生的注意力更集中?
(2)某些数学内容的课堂学习大致可分为三个环节:即“教师引导,回顾旧知——自主探索,合作交流——总结归纳,巩固提高”.其中重点环节“自主探索,合作交流”这一过程一般需要30分钟才能完成,为了确保效果,要求学习时的注意力指标数不低于40,请问这样的课堂学习安排是否合理?并说明理由.
-
5、如图,正方形ABCD 的边长为4,E 为AB 上一点,且AE=3 ,F 为BC 边上的一个动点,连接EF ,以EF 为边向左侧作等腰直角三角形FEG ,EG=EF,∠GEF=90°,连接AG ,则AG 的最小值为 .

-
6、某篮球架的侧面示意图如图所示,现测得如下数据:底部支架AB的长为1.74m,后拉杆AE的倾斜角∠EAB=53°,篮板MN到立柱BC的水平距离BH=1.74m,在篮板MN另一侧,与篮球架横伸臂DG等高度处安装篮筐,已知篮筐到地面的距离GH的标准高度为3.05m.则篮球架横伸臂DG的长约为m(结果保留一位小数,参考数据:sin53°≈ , cos53°≈ , tan53°≈).

-
7、已知是方程的一个解,则的值是 .
-
8、比例式中的值等于 .
-
9、如图,一次函数的图象和反比例函数的图象交于 , 两点,若 , 则的取值范围是( )
 A、 B、 C、或 D、或
A、 B、 C、或 D、或 -
10、我国古代著作《四元玉鉴》记载“买椽多少”问题:“六贯二百一十钱,倩人去买几株椽.每株脚钱三文足,无钱准与一株椽.”其大意为:现请人代买一批椽,这批椽的价钱为文.如果每株椽的运费是文,那么少拿一株椽后,剩下的椽的运费恰好等于一株椽的价钱,试问文能买多少株椽?设这批椽的数量为株,则符合题意的方程是( )A、 B、 C、 D、
-
11、“黔绣”的技师擅长在叶脉上飞针走绣,巧妙地将传统刺绣图案与树叶天然纹理完美结合,创作出神奇的“叶脉苗绣”作品.实际上很多叶片本身都蕴含着黄金分割的比例,在大自然中呈现出优美的样子.如图,点P是的黄金分割点(),如果长为 , 那么的长约为( ) .
 A、 B、 C、 D、
A、 B、 C、 D、 -
12、从甲地到乙地有三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:
公交车用时的频数
公交车用时
线路
合计
45
265
167
23
500
59
151
166
124
500
50
50
122
278
500
早高峰期间,乘坐哪条线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大( )
A、线路 B、线路 C、线路 D、不能确定 -
13、某商店的货架可抽象成如图所示的图形,其中 , , , , (单位:),则的长度是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
14、若、是一元二次方程的两根(),则( )A、-3 B、3 C、-10 D、10
-
15、在数学探究性学习中经常会用到从特殊到一般、类比化归等数学思想和方法,如下是一个具体的探究性学习案例,请完善整个探究过程.
问题呈现过点的直线为常数且分别交轴的正半轴和轴的正半轴于点和 , 探究并说明是定值.
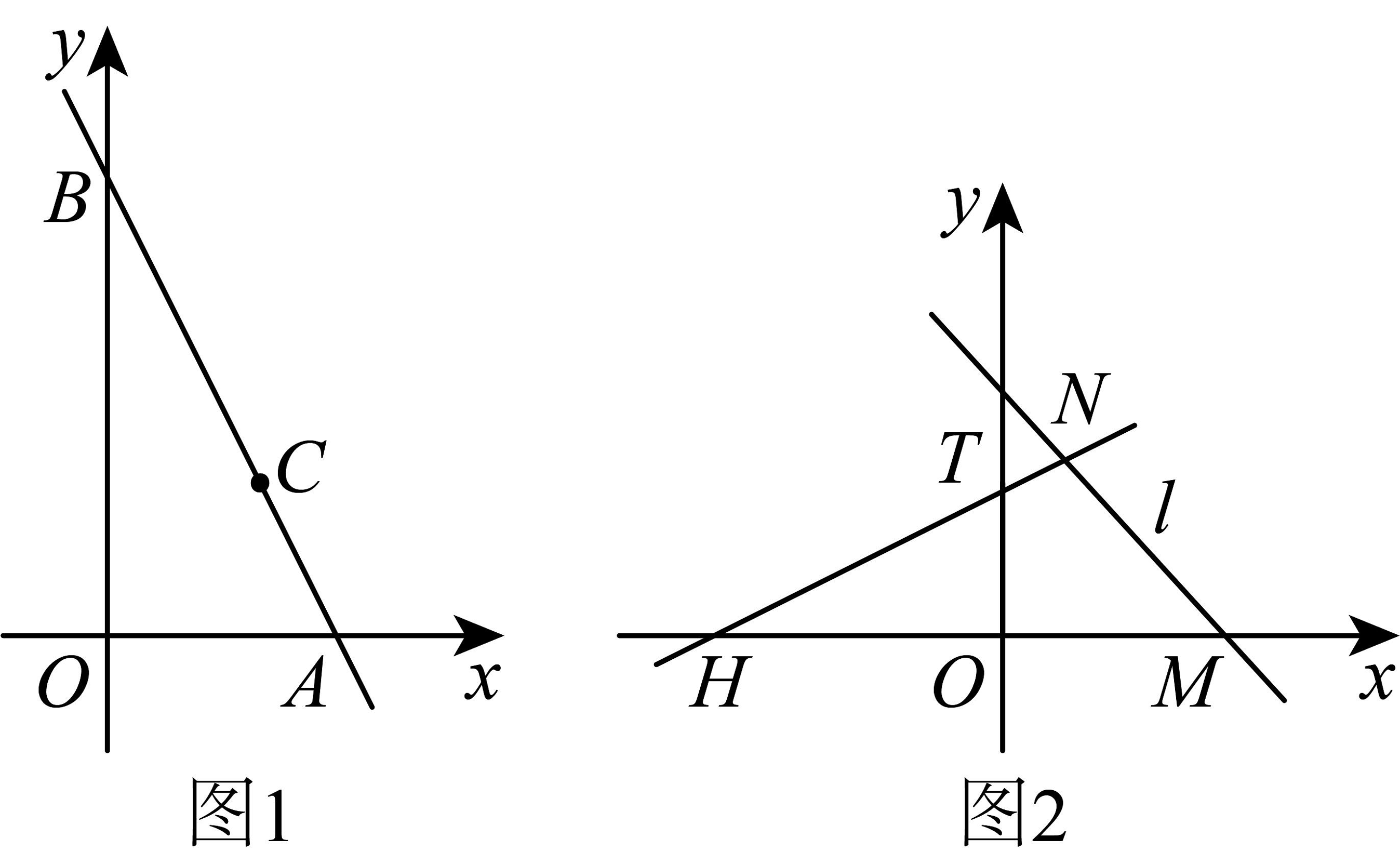 (1)、特例探究如图1,过点的直线分别交轴和轴于点和 , 求的值;(2)、一般证明
(1)、特例探究如图1,过点的直线分别交轴和轴于点和 , 求的值;(2)、一般证明①时,直接写出_____;
②求出的值;
(3)、类比推广如图2,已知 , 点在轴的正半轴上,过且不与轴平行的直线交直线于第一象限点 , 若总有 , 请探究:直线是否过定点,如果是,请求出定点坐标;如果否,请说明理由. -
16、如图1,在等边三角形中,点、分别在边、运动上,且满足 , 连接与相交于 .
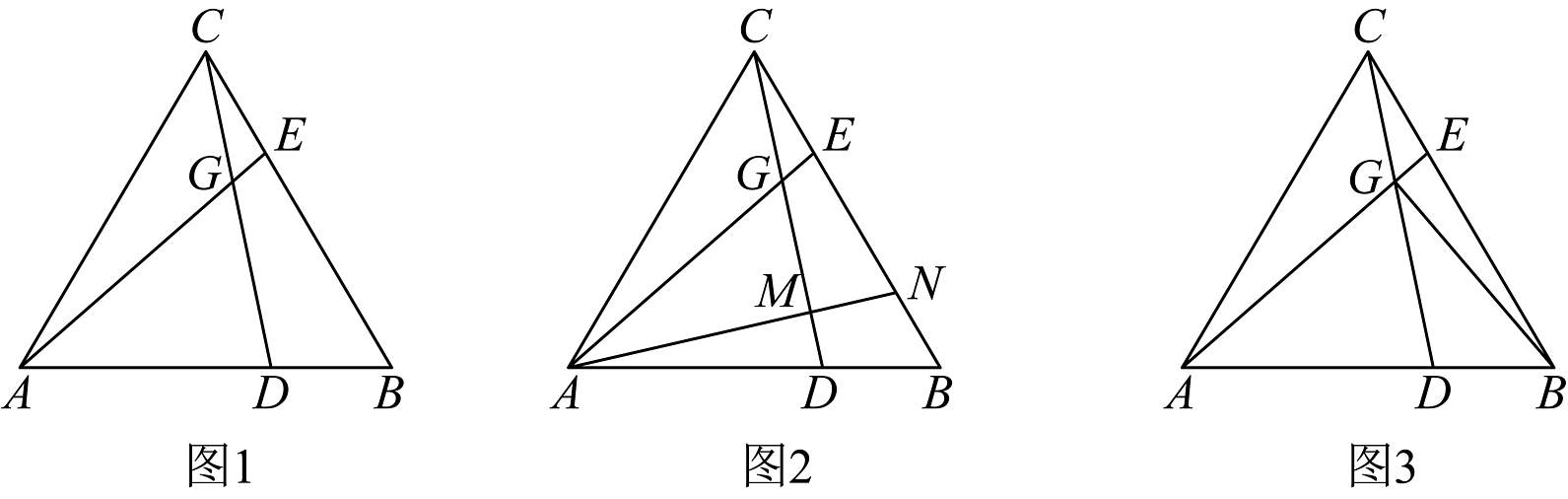 (1)、求证:;(2)、如图2,若边长为4,过点作 , 分别交、于、 , 设 , 求与的等量关系;(3)、如图3,在(2)问的条件下,连接 , 当时,求的长度.
(1)、求证:;(2)、如图2,若边长为4,过点作 , 分别交、于、 , 设 , 求与的等量关系;(3)、如图3,在(2)问的条件下,连接 , 当时,求的长度. -
17、在平面直角坐标系中,如果点到原点的距离为 , 点到点的距离是的倍(为正整数),那么称点为点的“倍共生点”.若点的坐标为时,如果点是点的“倍共生点”.且满足 , 那么的最大值为;如果点的坐标为 , 且在函数的图象上存在的“2倍共生点”,求出的取值范围 .
-
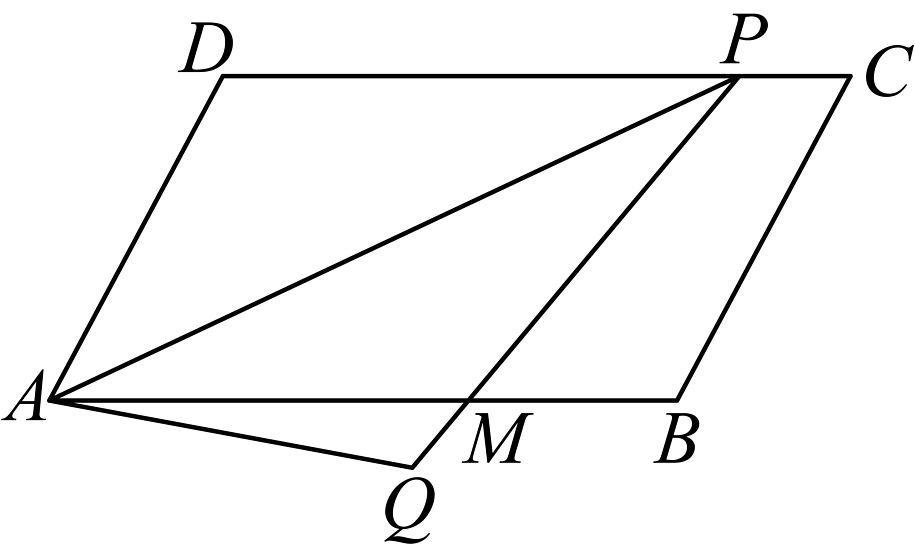
18、如图,平行四边形中, , 点为上一个动点,以为对称轴折叠得到 , 点的对应点为点 , 直线交于点 , 若 , 当点与点重合时,的长为 , 当有最小值时,的长为 .
-
19、已知 , 求代数式的值是 .
-
20、如图,直线与轴交于点 , 与轴交于点 , 点在轴上点的右边, , 经过点的直线与正比例函数的图象平行,直线与直线相交于点 , 点为直线上一动点.
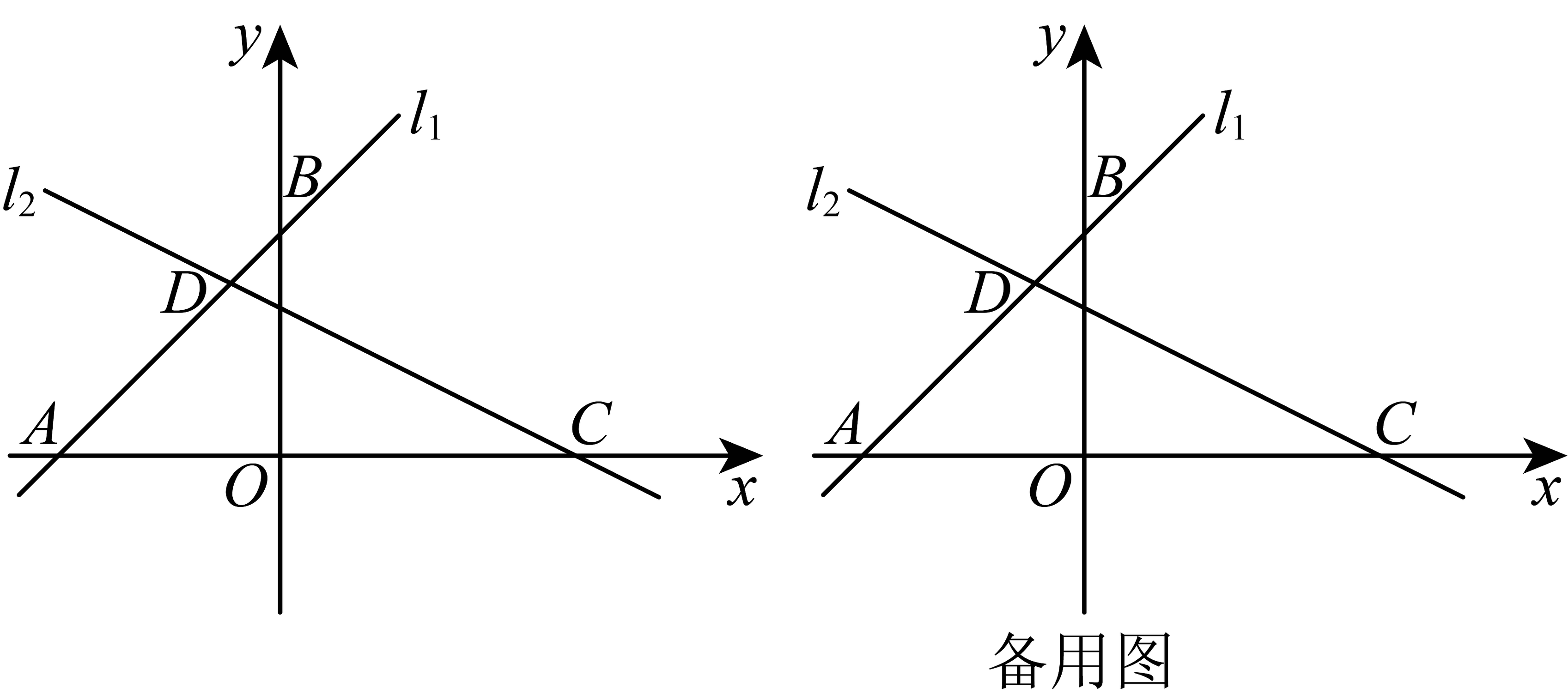 (1)、求点坐标;(2)、若 , 请求出点的坐标;(3)、若在平面内存在一点 , 使得四点、、、构成菱形,若存在,请直接写出点横坐标的值,若不存在,请说明理由.
(1)、求点坐标;(2)、若 , 请求出点的坐标;(3)、若在平面内存在一点 , 使得四点、、、构成菱形,若存在,请直接写出点横坐标的值,若不存在,请说明理由.