相关试卷

1、如图，□ABCD的对角线AC和BD相交于点O，BM，CM分别平分∠ABC，∠BCD，连接OM，若OM=1，AD= $\frac{2}{3}$ AB，则□ABCD的周长为.

查看解析
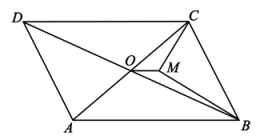
2、学习了《平面图形的镶嵌》后，某校8.1班数学兴趣小组打算用边长相同的正多边形纸板铺平面图形.如图，他们将2个正三角形纸板和1个正方形纸板绕点O放置.若在∠EOF处要无空隙、不重叠地拼1个正多边形纸板，则该正多边形纸板的边数为.

查看解析
3、已知直线y=（2-a）x+2a+1经过第一、三、四象限，则ａ的取值范围为.

查看解析
4、若a-3是多项式a²-a+k的一个因式，则常数k的值为.

查看解析
5、如图，在△ABC中，∠CAB=45°，CD，AE分别是边AB，BC上的高，连接DE，作DF⊥DE交AE于点F.

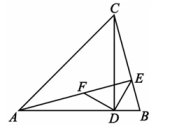(1)、求证：DF=DE；

(2)、请在图中作出△CDE关于直线BC对称的A△CGE，连接DG，求证：四边形DGEF是平行四边形；

(3)、若CE=2，∠EAB=15°，求DF的长.

查看解析
6、如图，在平面直角坐标系中，每个小方格都是边长为1个单位长度的正方形，△ABC的顶点坐标分别为A（2，-5），B（5，-3），C（3，-1）·

(1)、若 $△ A_{1} B_{1} C_{1}$ 和 $△ A B C$ 关于原点对称，请在图中画出 $△ A_{1} B_{1} C_{1}$ ；

(2)、请求出 $△ A_{1} B_{1} C_{1}$ 的面积；

(3)、将 $△ A_{1} B_{1} C_{1}$ 绕点M顺时针旋转 $9 0^{°}$ 得到 $△ A_{2} B_{2} C_{2}$ ，若 $C_{2} (0, 2)$ ，直接写出点M， $A_{2}$ ， $B_{2}$ 的坐标.

查看解析
7、先化简，再求值： $\frac{2 x + 1}{x^{2} - 1} \div \frac{x^{2} - x}{x^{2} - 2 x + 1} - \frac{1}{x + 1}$ ，其中 $x = - \frac{1}{3}$

查看解析
8、解不等式组： ${\begin{array}{l} \frac{2 x + 3}{4} - \frac{x}{3} < 1 ① \\ 2 (x + 3) \geq 3 - x ② \end{array}$ 并将解集在数轴上表示出来.

查看解析
9、

(1)、因式分解：2x²+12xy-8x；

(2)、解方程： $\frac{x}{2 x - 3} + \frac{5}{3 - 2 x} = 4$ .

查看解析
10、如图，直线y＝- $\frac{3}{4}$ x-3与x轴，y轴分别交于点M，N.现以点N为圆心，NM长为半径画弧，与y轴正半轴交于点P，则点P的坐标为.

查看解析
11、如图，在△ABC中，∠ACB=90°，∠B=60°，CD⊥AB于点D，且BD=2，则AD=.

查看解析
12、若x²+14x+49=（x+a）² ，则a的值为.

查看解析
13、若一个多边形的每一个外角都等于120°，则该多边形的内角和度数为.

查看解析
14、已知 $\frac{n}{m} = \frac{1}{2}$ ，则 $\frac{n}{m + n}$ 的值为.

查看解析
15、为了丰富同学们的课外社团活动，某学校增购了一批数量相等的乒乓球拍和羽毛球拍，供参加这些社团的学生使用，其中购买乒乓球拍用了1000元，购买羽毛球拍用了600元，已知每副乒乓球拍比每副羽毛球拍贵20元，设每副羽毛球拍x元，则符合题意的方程是（）

A、 $\frac{1000}{x + 20} = \frac{600}{x}$ B、 $\frac{1000}{x} = \frac{600}{x + 20}$ C、 $\frac{1000}{x - 20} = \frac{600}{x}$ D、 $\frac{1000}{x} = \frac{600}{x - 20}$

查看解析
16、在平面直角坐标系中，将点P（4，-5）向上平移6个单位后得到的对应点的坐标是（）

A、（4，1） B、（10，-5） C、（-2，-5） D、（4，-11）

查看解析
17、在下列多项式中，能用平方差公式进行因式分解的是（）

A、x²+y² B、-x²-y² C、x²-y² D、x²+2x+1

查看解析
18、如图，在△ABC中，AB=AC，AB的垂直平分线l交AC于点D，连接BD.若∠C=70°，则∠ABD=（）

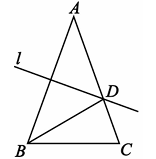A、35° B、40° C、45° D、50°

查看解析
19、若分式 $\frac{3}{x + 1}$ 无意义，则χ的取值是（）

A、x=3 B、x=1 C、x=0 D、x=-1

查看解析
20、如图，在△ABC中，AB＝AC，∠A=120°，则∠C的度数为（）

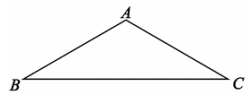A、20° B、25° C、30° D、35°

查看解析

上一页 655 656 657 658 659 下一页跳转