相关试卷
- 2017-2018学年北师大版数学八年级下册同步训练:6.4 多边形的内角和与外角和
- 2017-2018学年北师大版数学八年级下册同步训练:6.3 三角形的中位线
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.2 平行四边形的判定 ——用对角线的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.2.1 平行四边形的判定——用边的关系判定平行四边形
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:6.1 平行四边形的性质 课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.4分式方程课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.4 分式方程课时1
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时2
- 2017-2018学年北师大版数学八年级下册同步训练:5.3 分式的加减法 课时1
-
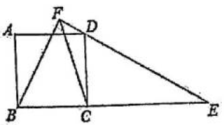
1、在数学拓展性学习课程《玩转学具》的课堂中,小陆同学发现:在一副三角尺中,含45°角的三角尺的斜边长与含 30°角的三角尺的长直角边的长相等.于是小陆同学提出一个问题:如图,将一副三角尺的直角顶点重合拼放在一起,点B,C,E在同一条直线上,若BC=2,则AF 的长为.

-
2、已知α为锐角,当 无意义时, sin(α+ .
-
3、 计算:(1)、(2)、
-
4、 在 Rt△ABC 中,∠C=90°,∠A =60°,则sinA+ cos B 的值为.
-
5、 在 Rt△ABC 中, 则∠B的度数为( )A、30° B、45° C、60° D、90°
-
6、计算 的结果是( )A、1 B、2 C、- 2 D、- 1
-
7、 如图,点E是正方形ABCD的BC延长线上一点,连接ED,过点B作交ED的延长线于点F,连接CF.
 (1)、 若 , , 求BF的长;(2)、 求证:.
(1)、 若 , , 求BF的长;(2)、 求证:. -
8、 在平面直角坐标系中,点A(-2,3)关于y轴的对称点为点B,连接AB,反比例函数的图象经过点B,过点B作轴于点C,点P是该反比例函数图象上任意一点.
 (1)、 求k的值;(2)、 若的面积等于2,求点P坐标.
(1)、 求k的值;(2)、 若的面积等于2,求点P坐标. -
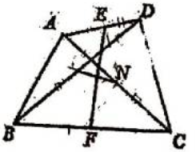
9、 如图,AC,BD是四边形ABCD的对角线, , 分别是AD,BC的中点, , 分别是BD,CA的中点. 求证:EF,MN互相平分.
-
10、 据调查,八年级某班30名学生所穿校服尺寸绘制如下条形统计图:
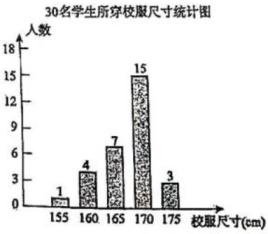 (1)、求这30名学生所穿校服尺寸的众数和中位数;(2)、若该校八年级共有600名学生,请你估计尺寸为170cm的校服需要多少件.
(1)、求这30名学生所穿校服尺寸的众数和中位数;(2)、若该校八年级共有600名学生,请你估计尺寸为170cm的校服需要多少件. -
11、 如图是由边长为1的小正方形构成的的网格,点A,B均在格点上.
 (1)、 在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、 在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上(画出一个即可).
(1)、 在图1中画出以AB为边且周长为的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)、 在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上(画出一个即可). -
12、解下列方程:(1)、(2)、
-
13、 如图,在四边形ABCD中, , 点E是AD的中点,作于点F,已知 , , 则EF的长为.

-
14、 如图,矩形ABCD中,E为BC中点,将沿直线AE折叠,使得点B落在点F处,连接FC.若 , 则=.
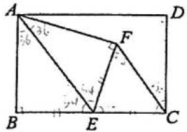
-
15、 数据1,3,5,12,a,其中整数a是这组数据中的中位数和众数,则该组数据的平均数是.
-
16、 如图,已知反比例函数的图象经过面积为8的矩形ABOC的顶点A,则k的值为.

-
17、 如果二次根式有意义,则的取值范围为.
-
18、 如图, 在▱ABCD中, AB=3, AD=4, , 过BC的中点E作 , 垂足为点F, 与DC的延长线相交于点H, 则的面积是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
19、 如图,矩形纸片ABCD中,点E是AD的中点,且 , BE的垂直平分线MN恰好过点C,则矩形的一边AB的长度为( )
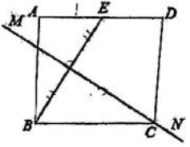 A、 B、 C、 D、2
A、 B、 C、 D、2 -
20、 用反证法证明命题“在直角三角形中,至少有一个锐角不大于时,首先应假设这个直角三角形中( )A、两个锐角都大于 B、两个锐角都小于 C、两个锐角都不大于 D、两个锐角都等于