相关试卷

1、先化简，再求值： $\frac{m^{2} - m}{m^{2} + 2 m + 1} \div (\frac{2}{m + 1} - \frac{1}{m})$ ，其中m满足 $m (m + 4) = - 4$ .

查看解析
2、

(1)、计算： $\sqrt[3]{- 8} - \sqrt{28} + | 2 - \sqrt{7} |$ .

(2)、化简： $(2 a + b)^{2} - (2 a + b) (2 a - b)$ .

查看解析
3、如图1，在Rt $△ A B C$ 中， $∠ C = 9 0^{°}$ ，动点P从点A出发，沿着 $A \to B \to C$ 的路径运动到点C停止，过点P作 $P Q ⊥ A C$ ，垂足为Q. 设点P的运动路程为x， $P Q - A Q$ 的值为y，y随x变化的函数图象如图2所示，则BC的长为.

查看解析
4、在平面直角坐标系xOy中，点A(4，0)，点P在过原点的直线l上，且 $A P = O P = 4$ ，则直线l的解析式是.

查看解析
5、如图，在正五边形ABCDE内，以AB为边作等边 $△ A B F$ ，再以点A为圆心， AE长为半径画弧. 若 $A B = 3$ ，则阴影部分的面积是.

查看解析
6、若关于x的一元二次方程 $k x^{2} - 2 x + 1 = 0$ 有两个不相等的实数根，请写出一个满足条件的k的值.

查看解析
7、如图，菱形ABCD的对角线AC，BD相交于点O， $A E ⊥ B C$ ，垂足为E，连接OE. 若 $B D = 6$ ， $O E = \sqrt{5}$ ，则菱形ABCD的面积是.

查看解析
8、如图，四边形ABCD是 $⊙ O$ 的外切四边形， $A B = 9$ ， $C D = 15$ .则四边形ABCD的周长为.

查看解析
9、如图，小明从A处沿东北方向走到B处，再从B处沿南偏东63°方向走到C处，则 $∠ A B C$ 的度数是.

查看解析
10、等腰三角形的两边长分别为3和7，则第三边长为.

查看解析
11、分解因式： $8 a b^{2} - 2 a =$ .

查看解析
12、如图，用四个全等的直角三角形拼成“赵爽弦图”，得到大正方形ABCD和小正方形EFGH，连接BD交CH于点P. 若 $B P = B C$ ，则 $t a n ∠ C B G$ 的值是（）

A、 $\sqrt{2} - 1$ B、 $2 - \sqrt{2}$ C、 $\frac{\sqrt{2}}{2}$ D、 $\frac{2 \sqrt{2}}{3}$

查看解析
13、如图，一次函数 $y_{1} = k_{1} x + b (k_{1} \neq 0)$ 的图象与两坐标轴分别交于点A， B，与反比例函数 $y_{2} = \frac{k_{2}}{x} (k_{2} \neq 0, x ＞ 0)$ 的图象交于点C(1，2)， D(m， $\frac{1}{2}$ ). 下列结论错.误的是（）

A、 $b = \frac{5}{2}$ B、 $△ B O C$ 与 $△ A O D$ 的面积相等 C、 $△ C O D$ 的面积是 $\frac{17}{4}$ D、当 $1 \leq x \leq 4$ 时， $y_{1} \geq y_{2}$

查看解析
14、如图，直线l和直线l外一点A，以点A为圆心，适当的长度为半径画弧，交直线l于点M，N；分别以点M，N为圆心，线段MN的长为半径画弧，两弧交于点P（点P与点A在直线l的两侧）；作直线AP交直线l于点O，连接AM，AN，PM，PN.根据以上作图过程，有以下结论：
① $△ A M N$ 是等边三角形；②AP垂直平分线段MN；③PA平分 $∠ M P N$ ；④四边形AMPN是菱形；⑤ $c o s ∠ M P N = \frac{1}{2}$ .
其中正确结论的个数是（）

A、2个 B、3个 C、4个 D、5个

查看解析
15、下列运算正确的是（）

A、 $(- 3)^{- 2} = 9$ B、 $2^{4} + 2^{9} = 8$ C、 $(5 \times 1 0^{3}) \times (4 \times 1 0^{2}) = 2 \times 1 0^{6}$ D、 $(- 2 \times 1 0^{2})^{3} = 8 \times 1 0^{6}$

查看解析
16、当 $x = 1$ 时，下列代数式在实数范围内有意义的是（）

A、 $\frac{\sqrt{x - 1}}{x - 1}$ B、 $\frac{\sqrt{x - 1}}{x}$ C、 $\frac{\sqrt{x - 2}}{x - 1}$ D、 $\frac{\sqrt{x - 2}}{x}$

查看解析
17、下列说法正确的是（）

A、概率很大的事件一定会发生 B、“任意画一个三角形，其外角和是360°”是必然事件 C、两组身高数据的方差分别是 $S_{甲}^{2} = 0.1$ ， $S_{乙}^{2} = 0.3$ ，则乙组的身高更整齐 D、某抽奖活动的中奖概率为 $\frac{1}{10}$ ，表示抽奖10次就有1次中奖

查看解析
18、在中国，鼓是精神的象征，舞是力量的表现，先贤孔子曾说过“鼓之舞之”，可见“鼓舞”一词起源之早. 如图1所示，鼓的主视图是（）

A、 B、 C、 D、

查看解析
19、下列四个实数中，最大的是（）

A、-7 B、0 C、 $\frac{1}{2}$ D、 $\sqrt{30}$

查看解析
20、已知抛物线y＝ax²＋bx－4过点A（－1，0），B（m ， 0），与y轴交于点C ．点B是x轴正半轴上的动点，点F是抛物线在第四象限图象上的动点，连接BC ， AF ，且AF交y轴于点D ，交BC于点E ．

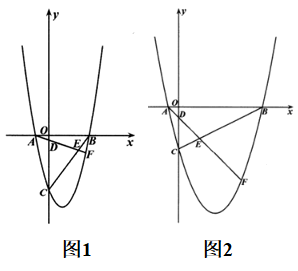(1)、当m＝3时，求抛物线的解析式；

(2)、如图1，在（1）的条件下，若∠CDE＝∠CED ，求直线AF的解析式；

(3)、要使得∠DCE＝∠DEC成立，请探索m的取值范围（直接写出结果）；

(4)、如图2，∠DCE＝∠DEC ，当m为何值时，OD的长度等于1?

查看解析

上一页 282 283 284 285 286 下一页跳转