-
1、说明命题“若 , 则”是假命题,可用的反例是( )A、 , B、 , C、 , D、 ,
-
2、不等式组的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
3、下列图形中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
4、已知三个顶点的坐标分别为 , , , 把先向右平移个单位长度,再向下平移个单位长度后得到 , 且点的对应点为 , 点的对应点为 , 点的对应点为 .
 (1)、在坐标系中画出和;(2)、画出关于原点对称的;(3)、求的面积.
(1)、在坐标系中画出和;(2)、画出关于原点对称的;(3)、求的面积. -
5、解方程:(1)、;(2)、 .
-
6、在平面直角坐标系中有三个点 , , , 点关于点的对称点为 , 点关于点的对称点为 , 点关于点的对称点为 , 若按此规律继续以、、为对称中心重复操作,依次得到 , , , , 则点的坐标为( )A、 B、 C、 D、
-
7、从地面竖直向上抛出一小球,小球的高度(单位:)与小球运动时间(单位:)之间的函数关系如图所示.则下列结论不正确的是( )
 A、小球在空中经过的路程是 B、小球运动的时间为 C、小球抛出时,刚好到达最高点 D、小球所能到达的最大高度为
A、小球在空中经过的路程是 B、小球运动的时间为 C、小球抛出时,刚好到达最高点 D、小球所能到达的最大高度为 -
8、如图,在中, ,
 (1)、求证:;(2)、以为边,作等边三角形 , 且点在的左侧,连接 , , . 求的面积.
(1)、求证:;(2)、以为边,作等边三角形 , 且点在的左侧,连接 , , . 求的面积. -
9、如图,在中, , 于 , 点、分别在线段、上,且平分 , 与交于点 .
 (1)、当、是等腰三角形时,求的大小;(2)、当 , , 求的大小.
(1)、当、是等腰三角形时,求的大小;(2)、当 , , 求的大小. -
10、如图,在中, .
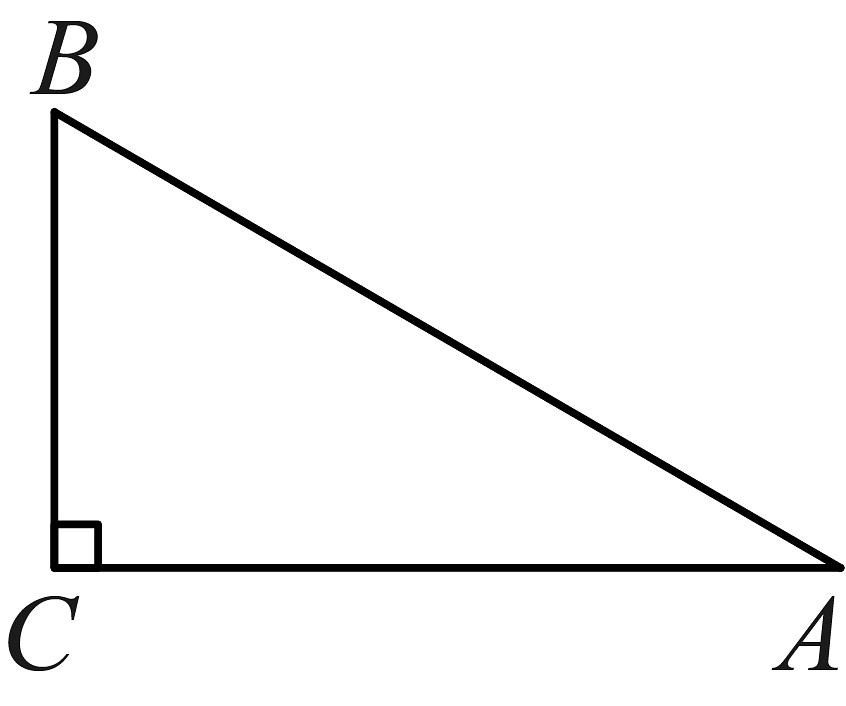 (1)、在边上找一点 , 使得点到边的距离与到边的距离相等(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(2)、在(1)的条件下,若 , , 求的面积.
(1)、在边上找一点 , 使得点到边的距离与到边的距离相等(尺规作图,保留作图痕迹,标注有关字母,不用写作法和证明);(2)、在(1)的条件下,若 , , 求的面积. -
11、如图,小明从点A出发,前进后向右转 , 再前进后又向右转 , …如此反复下去,直到她第一次回到出发点A,他所走的路径构成了一个正多边形.
 (1)、求小明一共走了多少米;(2)、求这个正多边形的内角和.
(1)、求小明一共走了多少米;(2)、求这个正多边形的内角和. -
12、如图,是的角平分线,平分 , 交于点E.
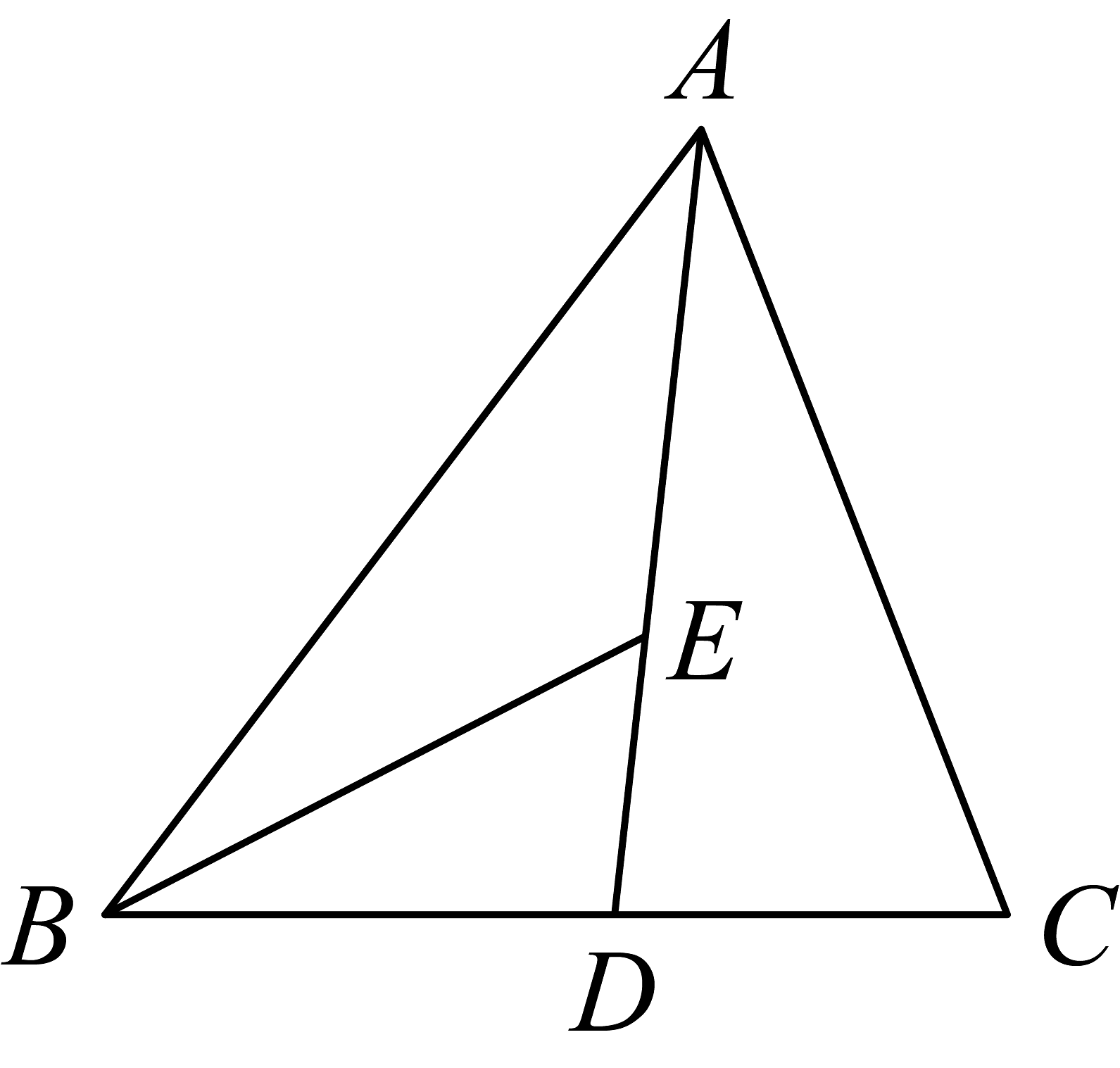 (1)、若 , 求的度数;(2)、直接写出与之间的数量关系.
(1)、若 , 求的度数;(2)、直接写出与之间的数量关系. -
13、如图,在中,的垂直平分线分别交于点 , 点 , 若点是直线上一动点,点是直线上的一动点, , , 则的最小值为 .

-
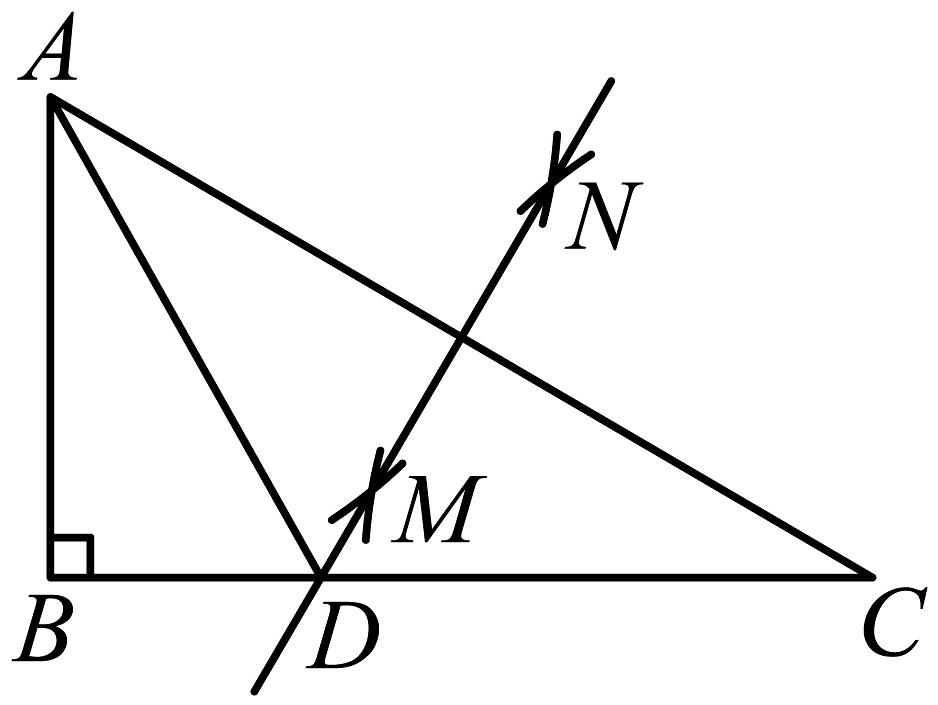
14、如图,在中, , 分别以点A和点C为圆心,大于的长为半径画弧,两弧相交于点M、N,作直线交于点D,连接 . 若 , 则 .
-
15、如图, , 点 , , 在同一直线上,若 , , 则的长为 .
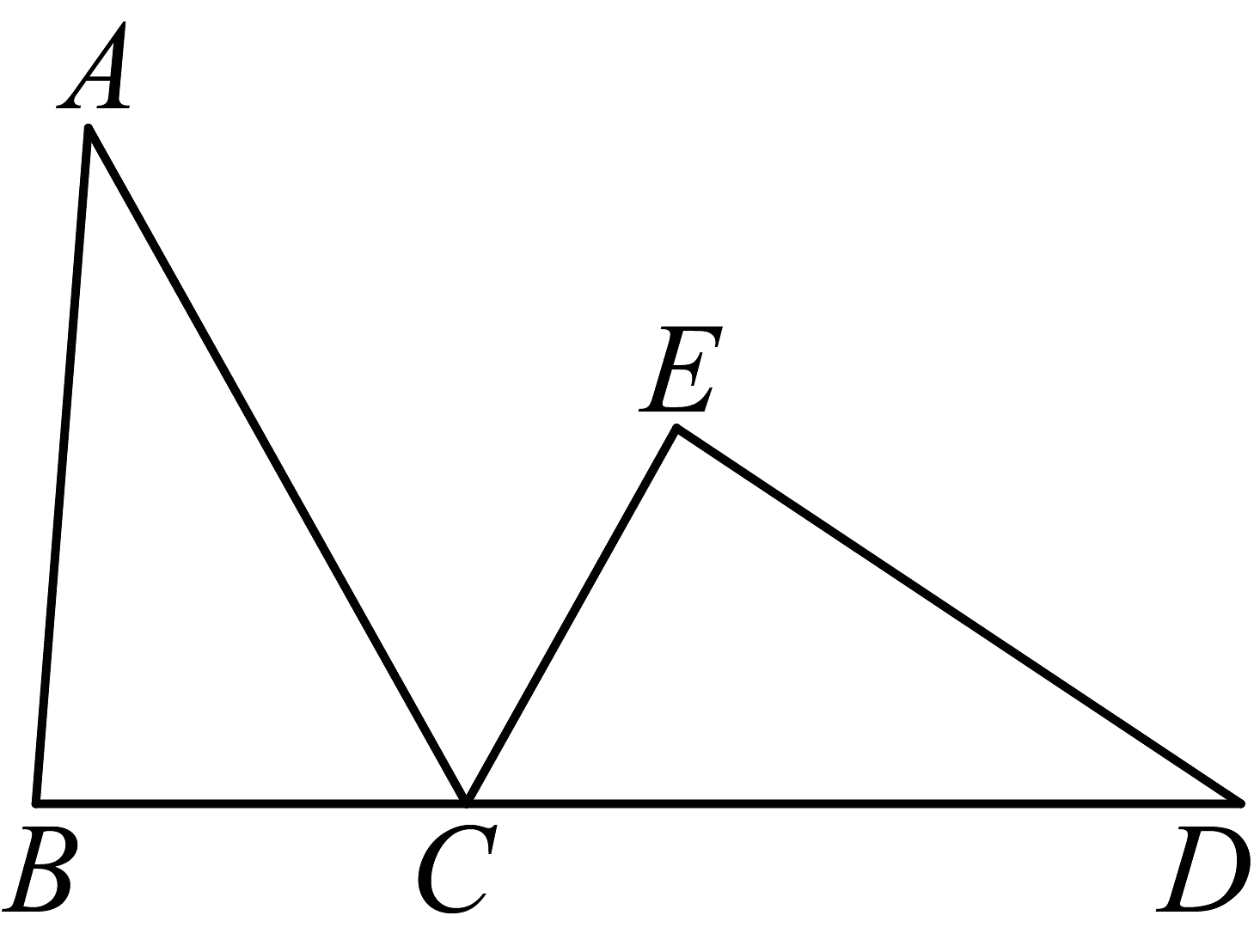
-
16、如图,在中, , 平分 , 交于点D, , 垂足为E.若 , 则的长为( )
 A、4 B、5 C、6 D、7
A、4 B、5 C、6 D、7 -
17、在下列图标中,可看作轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、如图所示,在中, , , , 点P由点A出发,沿边以的速度向点B移动;点Q由点B出发,沿边以的速度向点C移动.如果点P,Q分别从点A,B同时出发,问:
 (1)、经过几秒后,的面积等于?(2)、经过几秒后,;(3)、经过几秒后,两个三角形相似?
(1)、经过几秒后,的面积等于?(2)、经过几秒后,;(3)、经过几秒后,两个三角形相似? -
19、已知关于x的方程 .(1)、求证:此方程有两个不相等的实数根;(2)、设此方程的两个根分别为 , , 若 , 求m的值.
-
20、如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,的顶点都在格点上,建立平面直角坐标系.以原点O为位似中心,将放大,使变换后得到的三角形与原三角形对应边的比为 .
 (1)、请在网格内画出变换后图形,并写出各顶点的坐标;(2)、 .
(1)、请在网格内画出变换后图形,并写出各顶点的坐标;(2)、 .