-
1、近期,国产大模型强势崛起,在全球科技领域掀起热潮,随着、、豆包、讯飞星火等中国大模型的持续发展和广泛应用,未来中国将在全球领域扮演更加重要的角色市区某校信息科技课外实践小组为了调研该校学生对国产大模型应用场景的了解情况,从全校人中抽取了部分学生展开随机调查,调查结果分为四种:非常了解,比较了解,基本了解,不太了解,实践小组把此次调查结果整理并绘制成下面不完整的条形统计图和扇形统计图.
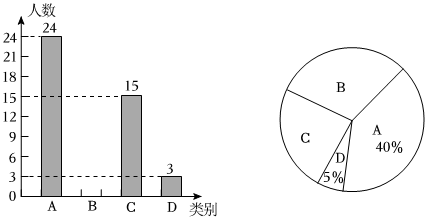
学生对国产大模型应用场景的了解情况
请结合图中所给的信息解答下列问题:
(1)、扇形统计图中所对应的扇形圆心角度数为;(2)、补全条形统计图;(3)、估计全校“比较了解”和“基本了解”国产大模型的应用场景的一共有多少人? -
2、解下列方程或方程组:(1)、;(2)、 .
-
3、如图,直线 , 被直线所截,连接 , , 与相交于点 , , .
 (1)、若 , 求的度数;(2)、点在上,连接 , 若 , 请判定与的数量关系,并说明理由.
(1)、若 , 求的度数;(2)、点在上,连接 , 若 , 请判定与的数量关系,并说明理由. -
4、解不等式,并将解集在数轴上表示出来.
.
-
5、在平面直角坐标系中,点的坐标是若点在第二象限,且点到轴的距离与到轴的距离相等,求的值.
-
6、计算: .
-
7、阅读理解:我们把称作二阶行列式,规定它的运算法则为 , 例如 , 如 , 则的取值范围是 .
-
8、九章算术中记载:今有共买物,人出八,盈三;人出七,不足四,问人数、物价各几何?译文:今有人合伙购物,每人出钱,会多钱:每人出钱,又会差钱,问人数、物价各是多少?设合伙人数为人,物价为钱,那么可列方程组为 .
-
9、若点在第四象限,那么的取值范围是 .
-
10、月日是世界读书日,某校为了解该校名七年级学生每周阅读课外书籍的时间,随机抽取了该校名七年级学生,调查了他们每周阅读课外书籍的时间,并制作成如图所示的频数分布直方图,那么估计该校七年级学生每周阅读课外书籍的时间不少于小时的学生约有名

-
11、甲、乙两人求二元一次方程的整数解,甲正确地求出一组解为 , 乙把看成 , 求得一组解为 , 则 , 的值为( )A、 B、 C、 D、
-
12、公司正在开发一款基于直角坐标系的导航软件为了测试软件的准确性,工程师在坐标系中设置了 , 两个关键点:若点在第四象限,则点在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
-
13、如图是篱笆围栏抽象出几何图形的一部分,则下列条件中能判断直线的是( )
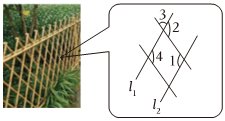 A、 B、 C、 D、
A、 B、 C、 D、 -
14、下列各项调查适合普查的是( )A、某班每位同学视力情况 B、黄河中现有鱼的种类 C、某市家庭年收支情况 D、某品牌灯泡使用寿命
-
15、“天宫课堂”第四课航天员演示了“水球变向实验”,水球的运动轨迹可表示为二元一次方程下列哪组解是这个二元一次方程的解( )A、 B、 C、 D、
-
16、下列各点在第四象限的点是( )A、 B、 C、 D、
-
17、如图,下列选项中的图案分别是奔驰、奥迪、大众、三菱汽车的车标,可以看作是由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、
-
18、我国是最早认识和使用负数的国家,下列各数中,最大的负数是( )A、 B、 C、 D、
-
19、已知 , 点 , 在直线上,点 , 在直线上,且于 .
 (1)、如图 , 求证:;(2)、如图 , 平分交于点 , 平分交于点 , 求的度数;(3)、如图 , 为线段上一点,为线段上一点,连接 , 为的角平分线上一点,且 , 则、、之间的数量关系是 .
(1)、如图 , 求证:;(2)、如图 , 平分交于点 , 平分交于点 , 求的度数;(3)、如图 , 为线段上一点,为线段上一点,连接 , 为的角平分线上一点,且 , 则、、之间的数量关系是 . -
20、某手机专卖店的一张进货单上有如下信息:款手机进货单价比款手机多元,花元购进款手机的数量与花元购进款手机的数量相同.(1)、求 , 两款手机的进货单价分别是多少元?(2)、某周末两天销售单上的数据,如表所示:
日期
款手机部
款手机部
销售总额元
星期六
星期日
求 , 两款手机的销售单价分别是多少元?
(3)、根据所给的信息,手机专卖店要花费元购进 , 两款手机若干部,问有哪几种进货方案?根据计算说明哪种进货方案获得的总利润最高.