相关试卷

1、已知n为正整数，则 $1^{n} + 2^{n} + 3^{n} + 4^{n}$ 末尾最多有个0.

查看解析
2、已知a为正整数，若关于x的方程x⁴+（a+5）x³+（3a+10）x²-4a-16=0有四个互不相同的整数根，则a=.

查看解析
3、若抛物线y=x²+bx+c与x轴、y轴交于三个不同的点A、B、C，当实数b、c变化时，△ABC的外接圆一定经过定点，此定点的坐标为.

查看解析
4、在平面直角坐标系xOy中，抛物线y=-x²+4x与x轴的正半轴交于点A，其顶点为M，点P是该抛物线上位于A、M两点之间的部分上的动点，过点P作PB⊥x轴于点B，PC⊥y轴于点C，且交抛物线于点D，连接BC，AD，OP，当四边形ABCD被OP分成的两部分面积比为1：2时，点P的坐标为.

查看解析
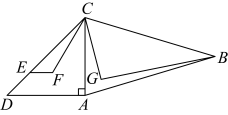
5、如图，∠BAC=∠BCD=90°，AC=2，三角形BCD面积始终为2，则AD的最大值为.

查看解析
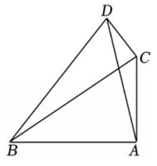
6、如图，△ABC是⊙O的内接三角形，将劣弧 $\overset{⌢}{A C}$ 沿AC折叠后刚好经过弦BC的中点D.若AC=6，∠C=60°，则⊙O的半径长为.

查看解析
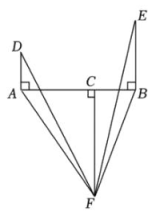
7、如图，点C在线段AB上，DA⊥AB，EB⊥AB，FC⊥AB，且DA=BC，EB=AC，FC=AB，∠AFB=53°，则∠DFE的度数是多少？

查看解析
8、试求方程x²-2x-4|x-1|+4=0的四个根之和；当t<5时，再求方程x²-2x-4|x-1|+b=0的四个根之和.

查看解析
9、已知a，b，c是三个非负数，并且满足3a+2b+c=5，2a+b-3c=1，设m=3a+b-7c，则m的最大值为.

查看解析
10、已知x²+3x+1=0，则-8x+2025=.

查看解析
11、已知a、b、c是实数，若（x²+2x+3)(3x²+4x-5)+（x²+x-4)²=（ax²+bx+lcl)² ，则代数式a+20b+23|c|的值为（）

A、0 B、1 C、-39 D、85

查看解析
12、如果方程 $(x - 1) (x^{2} - 2 x + m) = 0$ 的三根可作为一个三角形的三边之长，则实数m的取值范围是（）

A、 $0 \leq m \leq 1$ B、 $\frac{3}{4} \leq m$ C、 $\frac{3}{4} \leq m \leq 1$ D、 $\frac{3}{4} < m \leq 1$

查看解析
13、已知 $a = \frac{1 + \sqrt{5}}{2}$ ， $b = \frac{1 - \sqrt{5}}{2}$ ，则 $a^{10} + b^{10} =$ .

查看解析
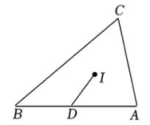
14、如图，在△ABC中，CB>AC，∠BAC=α，∠ABC=β，D为AB上一点，且CB-CA=BD，I为△ABC的三条角分线交点，则∠IDA=（）

A、 $\frac{1}{2} α$ B、 $90 ° - β$ C、β D、 $90 ° - \frac{1}{2} β$

查看解析
15、已知方程2|x|-k=kx-3无负数根，那么k的取值范围是（）

A、-2≤k≤3 B、2<k≤3 C、2≤k≤3 D、k≥3或k≤2

查看解析
16、设 $a = \frac{1^{2}}{1} + \frac{2^{2}}{3} + \frac{3^{2}}{5} + ⋯ \frac{101 2^{2}}{2023}$ ， $b = \frac{1^{2}}{3} + \frac{2^{2}}{5} + \frac{3^{2}}{7} + ⋯ \frac{101 2^{2}}{2025}$ ，则以下四个选项中最接近 $a - b$ 的整数为（）

A、253 B、506 C、1012 D、2023

查看解析
17、已知，在 $△ A B C$ 中， $∠ B A C \neq 90 °$ ， $∠ A C B = 45 °$ ， $B D$ ， $C E$ 均为 $△ A B C$ 的高，点F是射线 $B C$ 上一点，且 $A B = A F$ ，直线 $B D$ ， $C E$ 交于点G ．

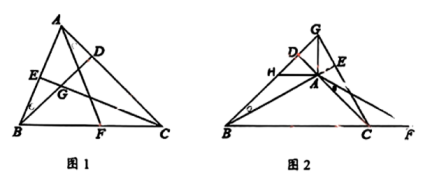(1)、【初步感知】
如图1，当 $∠ B A C < 90 °$ 时，试说明 $∠ A B D = ∠ C A F$ ；

(2)、【深入探究】
如图2，当 $∠ B A C > 90 °$ 时，连接 $A G$ ，试探究 $A G$ 与 $C F$ 的数量关系；

(3)、【拓展延伸】
连接 $D F$ ，若 $B G = 10$ ， $△ B D F$ 的面积为m ，求 $△ A C F$ ．面积（用含m的代数式表示）．

查看解析
18、通过 $A I$ 与机器人技术的结合，快递分拣实现了从“人工识别 $+$ 粗放操作”到“智能识别 $+$ 精准作业”的升级，大幅提升了效率和准确性．某 $A I$ 快递公司研发了两款智能分拣机器人甲和乙．现对一批包裹进行分拣，已知甲、乙两机器人分拣总数均为3000个，其分拣包裹数量y（单位：个）与工作时间x（单位：分钟）的关系如图所示．

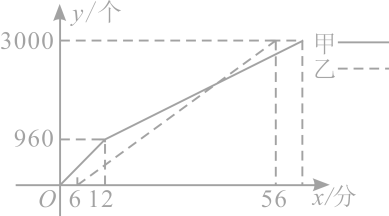(1)、乙机器人分拣包裹的速度是个/分，12分钟时，甲和乙机器人分拣的包裹数量相差个．

(2)、由于包裹条码破损，甲机器人视觉系统识别异常，降低了分拣速度，降速后甲机器人的分拣速度是最初分拣速度的 $50 %$ ，求甲和乙机器人分拣的包裹数量相同时的时间．

(3)、求整个分拣过程中两机器人分拣数量差不超过200个的总持续时间．

查看解析
19、小聪在学习完乘法公式后，发现完全平方公式通过代数变形，可以解决很多数学问题，例如：已知 $a + b = 7$ ， $a b = 4$ ，求 $a^{2} + b^{2}$ 的值．答案解： $∵ a + b = 7$ ； $∴ {(a + b)}^{2} = 7^{2} = 49$ ； $∴ a^{2} + b^{2} = {(a + b)}^{2} - 2 a b = 41$ 根据上面的解题思路与方法，解决下列问题：

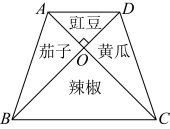(1)、已知 $a - b = 4$ ， $a b = 3$ ，求 ${(a + b)}^{2}$ 的值；

(2)、为贯彻《关于全面加强新时代大中小学劳动教育的意见》的方针政策，帮助同学们更好地理解劳动的价值与意义，培养学生的劳动情感、劳动能力和劳动品质，天府新区某校开垦了如图所示的一块梯形空地 $A B C D$ 作为劳动实践基地，并分成四块．其中， $A C ⊥ B D$ 于点O ， $O A = O D, O B = O C$ ．计划在 $△ A O B$ 和 $△ C O D$ 区域内组织同学们种茄子和黄瓜，在 $△ A O D$ 和 $△ B O C$ 的区域内种豇豆和辣椒，经测量，种豇豆和辣椒区域的面积和为 $84.5$ 平方米， $A C = 17$ 米，求种茄子和黄瓜区域的面积和是多少平方米．

查看解析
20、如图，在四边形 $A B C D$ 中， $A B = B C$ ， $A D = 3$ ， $∠ D = 45 °$ ， $A C ⊥ A D$ ，点E在边 $C D$ 上，且 $C E = C A$ ，四边形 $A B C D$ 的面积为12．点F为四边形内部一点，连接 $E F$ ，且 $E F ∥ A D$ ，连接 $C F$ ，将 $C F$ 绕点C逆时针旋转 $45 °$ 得到 $C G$ ，连接 $B G$ ，当 $C G$ 取得最小值时， $△ B C G$ 的面积为．

查看解析

上一页 365 366 367 368 369 下一页跳转