-
1、为迎接湖南师大附中梅溪湖中学办学十周年庆,某校友为母校设计了一款纪念版文化衫,原计划每件的售价为元,经过校友意见征集后,连续两次降价,最终每件的售价为元,并且每次降价的百分率相同.(1)、求该文化衫每次降价的百分率;(2)、若该文化衫每件的成本价为元,两次降价后,至少要售出多少件,总利润才能不低于元?
-
2、如图,在四边形中, , , 对角线 , 相交于点 .
 (1)、求证:四边形是平行四边形;(2)、若 , , , 求的长
(1)、求证:四边形是平行四边形;(2)、若 , , , 求的长 -
3、如图,在平面直角坐标系中,一直线与轴相交于点 , 与轴相交于点 , 与正比例函数的图象交于点 .
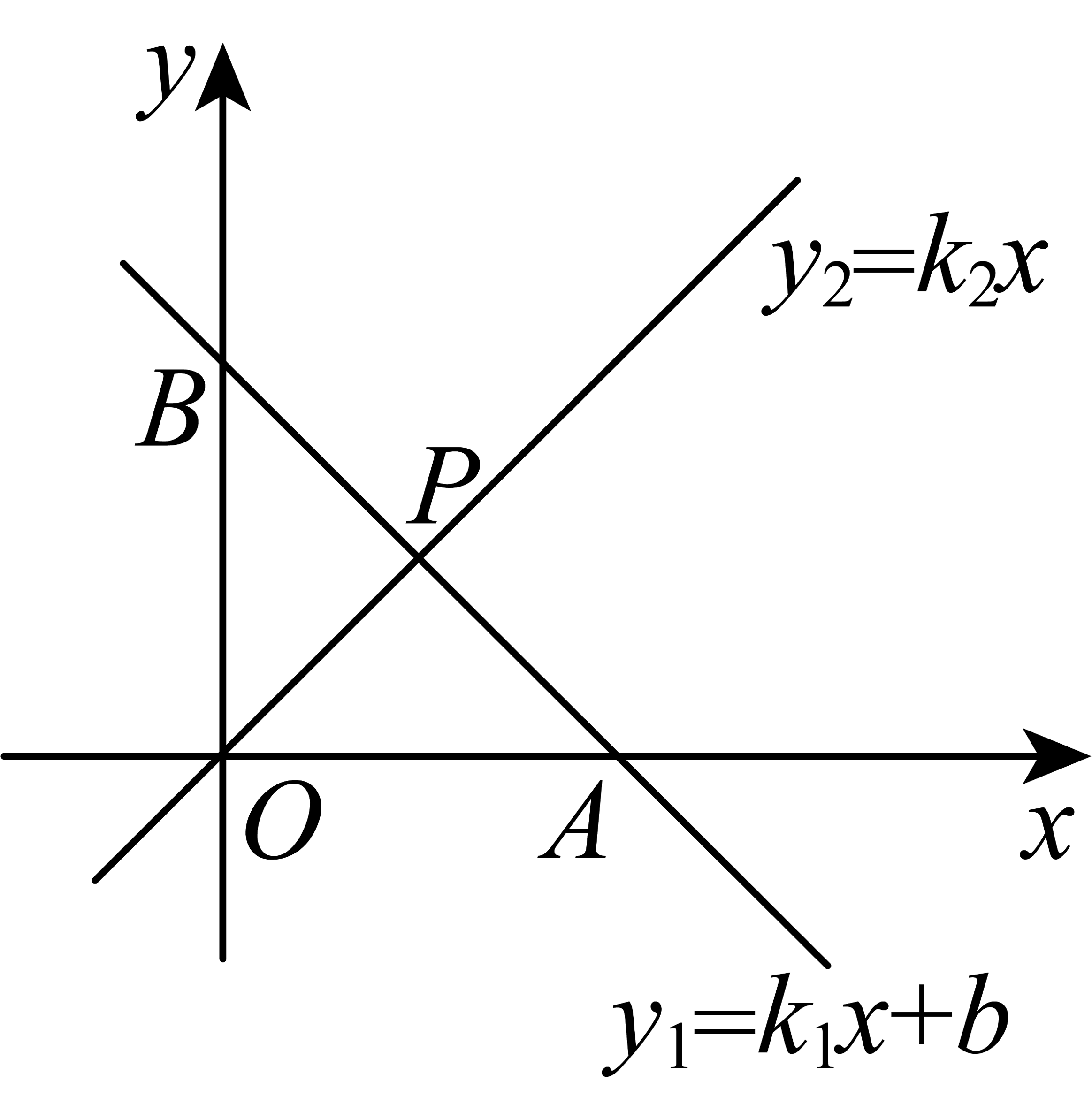 (1)、求直线的解析式.(2)、直接写出的解集.
(1)、求直线的解析式.(2)、直接写出的解集. -
4、“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲,如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形.设直角三角形较长直角边长为a,较短直角边长为b,若 , 大正方形的面积为25,则小正方形的边长为 .

-
5、如图,在平面直角坐标系中,一次函数与(、为常数,且)的图象交点的横坐标为3,则关于、的二元一次方程组的解为

-
6、某中学将晨练及体育课外活动、期中成绩、期末成绩按照的比例确定学期体育综合成绩.若小云这三项的成绩(百分制)依次是95,90,80,则小云这学期的体育综合成绩是 .
-
7、在函数中,自变量的取值范围是 .
-
8、如图,在平行四边形中,的平分线和的平分线交于上一点 , 若 , 则的长为( )
 A、 B、5 C、 D、
A、 B、5 C、 D、 -
9、一次函数的图像与轴的交点坐标为( )A、 B、 C、 D、
-
10、点关于y轴对称的点的坐标是( )A、 B、 C、 D、
-
11、如图1,在平面直角坐标系中,一次函数的图象与轴、轴分别相交于点、 , 以为边作正方形 , 反比例函数的图象在第一象限经过点 .
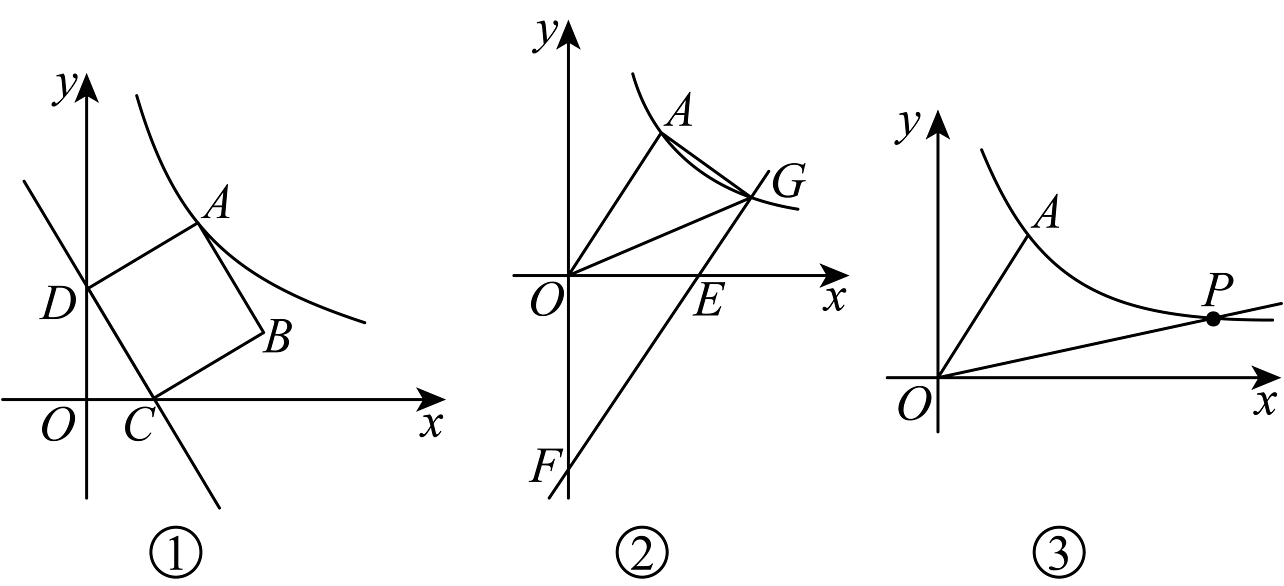 (1)、直接写出点、、的坐标及的值;(2)、如图②,将直线向下平移得到直线 , 交轴于点 , 交轴于点 , 交的图象于点 , 若 , 求直线的解析式;(3)、如图③,将直线绕点顺时针旋转后与第一象限的双曲线交于点 , 求点的横坐标.
(1)、直接写出点、、的坐标及的值;(2)、如图②,将直线向下平移得到直线 , 交轴于点 , 交轴于点 , 交的图象于点 , 若 , 求直线的解析式;(3)、如图③,将直线绕点顺时针旋转后与第一象限的双曲线交于点 , 求点的横坐标. -
12、【阅读】
三角形中位线定义:在中,若点分别是与的中点.则是的中位线.
三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
(1)、【定理证明】证明三角形的中位线定理的方法有多种.我们可以延长至 , 使得 , 连接 , 再利用全等三角形、平行四边形的知识进行证明,请结合图2,完成证明.
已知:在中,点 , 分别是 , 的中点.
求证: , 且 .
 (2)、【定理应用】
(2)、【定理应用】①顺次连接菱形四条边的中点所得的四边形一定是( )
A.平行四边形 B.菱形 C.矩形 D.正方形
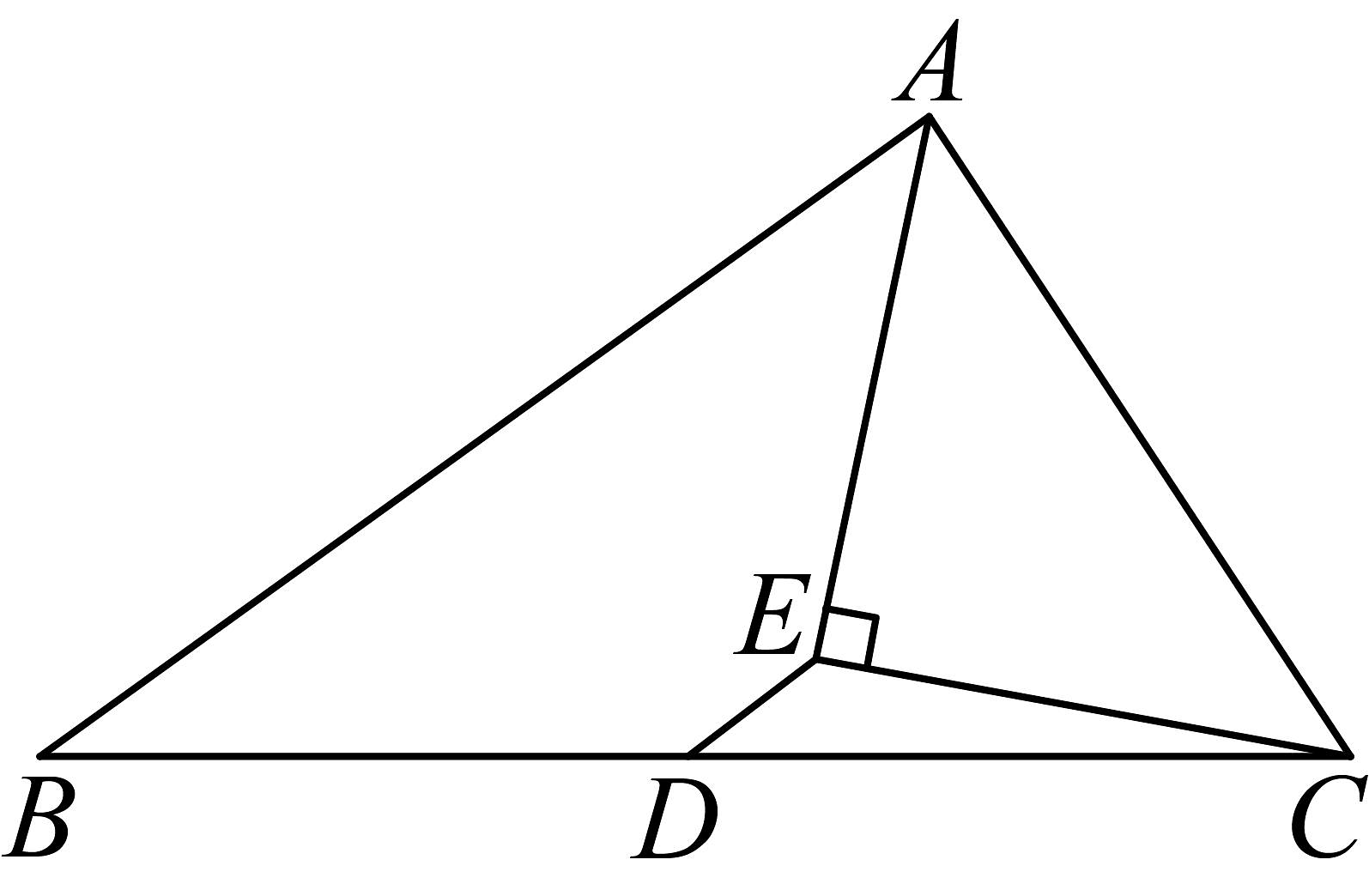
②在中,是边的中点,是的平分线,于点 , 连接 . 若 , , 求的长.
-
13、年初随着电影《哪吒之魔童闹海》的热播,与之相关的手办成了许多人热衷的收藏品.某批发商购进哪吒、敖丙两种挂件,进价和售价见表,且用320元购买敖丙挂件的个数与用400元购买哪吒挂件个数一样多.
敖丙挂件
哪吒挂件
进价(元/个)
售价(元/个)
11
15
 (1)、求的值(2)、若该批发商计划购进哪吒、敖丙两种挂件共1000件,其中敖丙挂件个,两种挂件全部销售后获得的利润为元,该批发商最多投入资金8600元用来采购且全部销售后利润不低于3500元,
(1)、求的值(2)、若该批发商计划购进哪吒、敖丙两种挂件共1000件,其中敖丙挂件个,两种挂件全部销售后获得的利润为元,该批发商最多投入资金8600元用来采购且全部销售后利润不低于3500元,求①与的函数关系式
②该批发商采取何种进货方案获利最大,最大利润是多少元?
-
14、已知:如图,在中, , 是外角的平分线, , 垂足为点 .
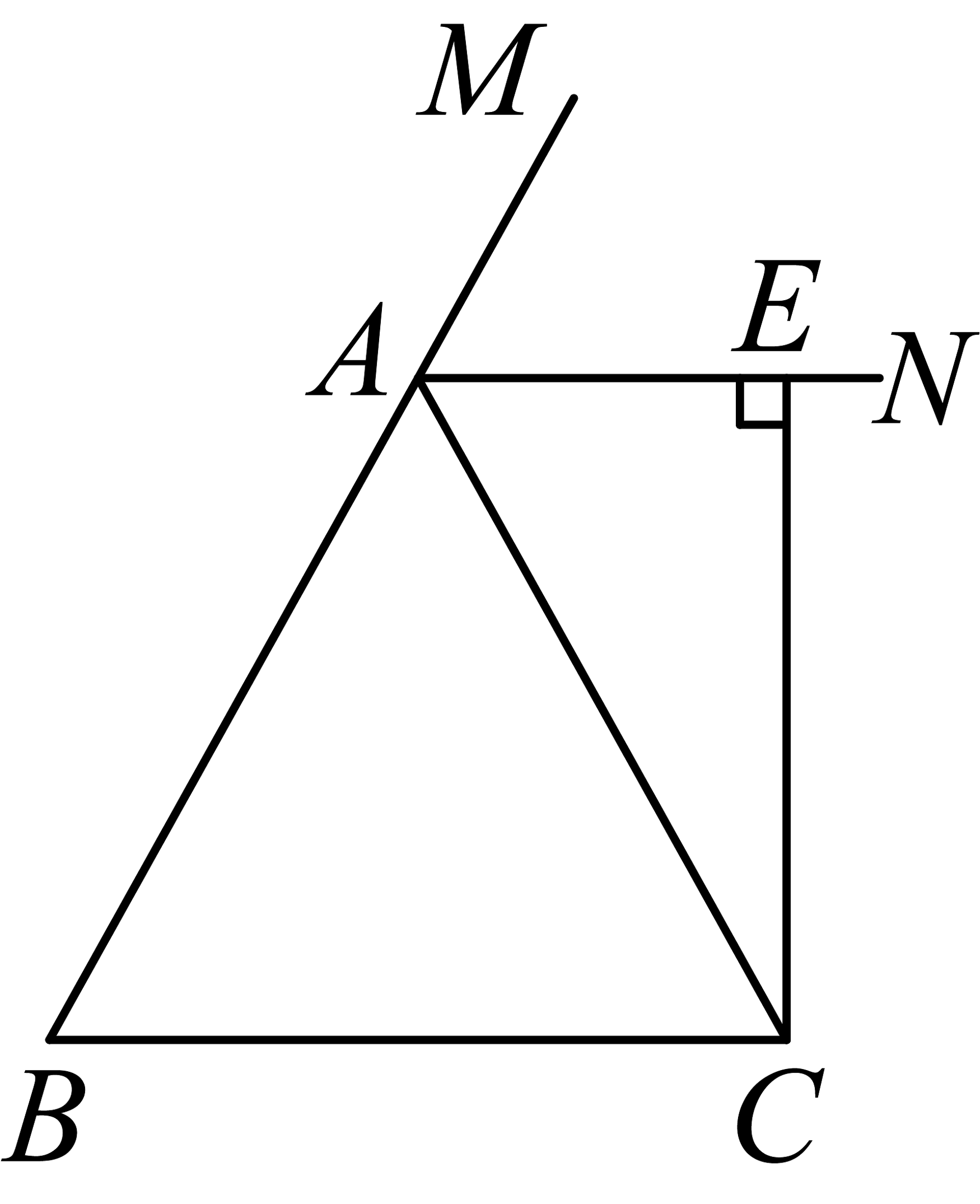 (1)、用尺规完成以下基本作图:作的角平分线,交于点 . (保留作图痕迹,不写作法)(2)、在(1)的基础上求证:四边形为矩形;
(1)、用尺规完成以下基本作图:作的角平分线,交于点 . (保留作图痕迹,不写作法)(2)、在(1)的基础上求证:四边形为矩形; -
15、我市某学校为推动“五育”并举,提高学生的综合素质,老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动.
【收集、整理数据】同学们随机收集桂花树、香樟树的树叶各1片,通过测量得到这些树叶的长(单位:),宽(单位:)的数据后,分别计算长宽比,整理数据如下:
1
2
3
4
5
6
7
8
9
10
桂花树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
香樟树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【分析数据】
平均数
中位数
众数
方差
桂花树叶的长宽比
3.74
4.0
0.0424
香樟树叶的长宽比
1.95
2.0
0.0669
【应用数据】
(1)、上述表格中: , ;(2)、甲同学说:“从树叶的长宽比的方差来看,我认为桂花树叶的形状差别大.”乙同学说:“从树叶的长宽比的平均数、中位数和众数来看,我发现香樟树叶的长约为宽的两倍.”哪位同学的说法合理?答: .
(3)、现有一片长 , 宽的树叶,请判断这片树叶更可能来自于桂花、香樟中的哪种树?并给出你的理由. -
16、计算或解方程(1)、计算:;(2)、计算;(3)、解方程;(4)、先化简,再求值: , 其中 , 选取一个合适的整数.
-
17、如图,是函数的图象上一点,直线分别交轴、轴于点、 , 过点作轴于点 , 交于点 , 作轴于点 , 交于点 , 当时,的值为 .

-
18、观察下列一串单项式: , , , , …,则第10个单项式为 .
-
19、将直线向上平移个单位长度后与直线交于点 , 则方程的解为 .
-
20、已知平行四边形的周长是20,相邻两边的长度相差2,则该四边形的较长边的长度为 .