相关试卷

1、如图，用两个边长为 $\sqrt{8}$ cm的小正方形纸片剪拼成一个大的正方形纸片.

(1)、大正方形纸片的边长是cm.

(2)、若沿此大正方形纸片边的方向剪出一个长方形纸片，能否使剪出的长方形纸片的长、宽之比为3∶2，且面积为12 cm²?若能，试求出剪出的长方形纸片的长、宽；若不能，试说明理由.( $\sqrt{2}$ ≈1.414)

查看解析
2、求下列各式中x的值：

(1)、 2(x-1)²-18=0.

(2)、 2(x-1)³=- $\frac{125}{4}$ .

查看解析
3、设a= $\frac{\sqrt{3} -1}{2}$ ， b= $\frac{1}{2}$ ， c= $\frac{\sqrt{3}}{2}$ ， d=4.

(1)、比较a与b两个数的大小.

(2)、求|a-b|+c- $\sqrt{d}$ 的值.

查看解析
4、已知下列实数： $\sqrt[3]{-216}$ ， |-1.5|，- $\frac{5}{2}$ ， 0， $\sqrt{12}$ ， (-2)².

(1)、在数轴上画出这些数的对应点，并用“<”把这些数连接起来.

(2)、设这些数的相反数在数轴上的对应点依次为A，B，C，D，E，F，在数轴上画出上述各点的位置.

查看解析
5、把下列实数填在相应的大括号内： ${(\frac{1}{10})}^{-3}$ ， -(+0.82)，-30 $\frac{1}{2}$ ， 3.14，- $\sqrt{25}$ ， 0，-2 025，- $\sqrt[3]{36}$ ， $|- \frac{3}{7}|$ ， - $\frac{π}{4}$ ， 2.101 001 000 1…(每两个1之间依次多一个0).
正分数：{                    …}；
整数：{                    …}；
负数：{          …}；
非正整数：{                    …}；
无理数：{            …}.

查看解析
6、 $\sqrt[3]{x + 4}$ 与 $\sqrt[3]{- 2 y -4}$ 互为相反数，则 $\frac{x}{y}$ 的算术平方根为.

查看解析
7、直田七亩半，忘了长和短.记得立契时，长阔争一半.今问俊明公，此法如何算.意思是：有一块面积为7亩半的长方形田，忘了长与宽各是多少.只记得在立契约的时候说过，宽是长的一半.现在请你帮他算出它的长是步.(一亩=240平方步)

查看解析
8、在数轴上，点A表示 $\sqrt{{(-5)}^{2}}$ ，点B与点A位于原点的两侧，且与原点的距离相等，则点B表示的数是.

查看解析
9、正整数a，b分别满足 $\sqrt[3]{53}$ <a< $\sqrt[3]{98}$ ， $\sqrt{2}$ <b< $\sqrt{7}$ ，则b^a=( )

A、4 B、8 C、9 D、16

查看解析
10、观察表格中的数据：
x
32
33
34
35
36
37
38
x²
1 024
1 089
1 156
1 225
1 296
1 369
1 444
由表格中的数据可知 $\sqrt{12.69}$ ( )

A、在3.4和3.5之间 B、在3.5和3.6之间 C、在35和36之间 D、在0.35和0.36之间

查看解析
11、如图，有一个数值转换器，当输入的x为4时，输出的y是( )

A、4 B、2 C、 $\sqrt{2}$ D、- $\sqrt{2}$

查看解析
12、如图，数轴上A，B两点所对应的实数分别是-π，1.若线段CB=2AB，则点C所表示的实数是( )

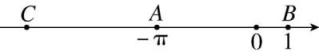A、π+1 B、-2π C、-2π-1 D、-2π-2

查看解析
13、下列各组数中互为相反数的是( )

A、-2与 $\sqrt{(-2)^{2}}$ B、-2与 $\sqrt[3]{-8}$ C、-2与- $\frac{1}{2}$ D、2与|-2|

查看解析
14、下列表格中关于有理数“2”的描述，错误的是( )
原数
相反数
倒数
绝对值
平方根
2
①-2
② $\frac{1}{2}$
③2
④ $\sqrt{2}$

A、① B、② C、③ D、④

查看解析
15、下列是无理数的为( )

A、- $\sqrt{13}$ B、- $\frac{2}{3}$ C、0 D、1.7 $\overset{·}{3}$

查看解析
16、一个数的相反数是最大的负整数，则这个数的平方根是( )

A、-1 B、1 C、±1 D、0

查看解析
17、在有理数-3，∣-3∣，(-3)² ， $\sqrt{(-3)^{2}}$ 中，负数有( )

A、1个 B、2个 C、3个 D、0个

查看解析
18、通过对如图数学模型的研究学习，解决下列问题：

(1)、如图①， $∠ B A D = 90^{\circ}$ ， $A B = A D$ ，过点 $B$ 作 $B C ⊥ A C$ 于点 $C$ ，过点 $D$ 作 $D E ⊥ A C$ 于点 $E$ .由 $∠ 1 + ∠ 2 = ∠ 2 + ∠ D = 90^{\circ}$ ，得 $∠ 1 = ∠ D$ .又 $∠ A C B = ∠ A E D = 90^{\circ}$ ， $A B = A D$ ，可以推理得到 $△ A B C ≌ △ D A E$ .进而得到 $A C =$ ， $B C = A E$ .我们把这个数学模型称为“ $K$ 字”模型或“一线三等角”模型；

(2)、如图②， $∠ B A D = ∠ C A E = 90^{\circ}$ ， $A B = A D$ ， $A C = A E$ ，连接 $B C$ ， $D E$ ，且 $B C ⊥ A F$ 于点 $F$ ， $D E$ 与直线 $A F$ 交于点 $G$ .求证：点 $G$ 是 $D E$ 的中点；

(3)、如图③，已知四边形 $A B C D$ 和四边形 $D E G F$ 均为正方形， $△ A F D$ 的面积为 $S_{1}$ ， $△ D C E$ 的面积为 $S_{2}$ ， $S_{1} + S_{2} = 10$ .求出 $S_{1}$ 的值.

查看解析
19、已知：在 $△ A B C$ 中， $A C = B C$ ， $∠ A C B = 90^{\circ}$ ，点 $D$ 是 $A B$ 的中点，点 $E$ 是 $A B$ 边上一点.

(1)、若 $B F ⊥ C E$ 于点 $F$ ，交 $C D$ 于点 $G$ （如图①）.求证： $A E = C G$ .

(2)、若 $A M ⊥ C E$ ，交 $C E$ 的延长线于点 $H$ ，交 $C D$ 的延长线于点 $M$ （如图②），找出图中与 $B E$ 相等的线段，并证明.

查看解析
20、如图，已知正方形 $A B C D$ ，从顶点 $A$ 引两条射线分别交 $B C$ ， $C D$ 于点 $E$ ， $F$ ，且 $∠ E A F = 45^{\circ}$ .求证： $B E + D F = E F .$

查看解析

上一页 411 412 413 414 415 下一页跳转

原数	相反数	倒数	绝对值	平方根
2	①-2	② $\frac{1}{2}$	③2	④ $\sqrt{2}$

x	32	33	34	35	36	37	38
x²	1 024	1 089	1 156	1 225	1 296	1 369	1 444