-
1、自变量与因变量的关系如图,当x增加1时,增加 .

-
2、关于的一元二次方程解的情况分析正确的是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定
-
3、第九届亚冬会于2025年2月7日至2月14日在我国冰城哈尔滨胜利召开.徽章作为亚冬会第一批特许商品早于2024年2月4日开售,并深受大家的喜爱.某商店以每枚45元的价格购进某款亚冬会徽章,以每枚68元的价格出售,经统计,2024年2月份的销售量为256枚,2024年4月份的销售量为400枚.(1)、求该款徽章2024年2月份到4月份销售量的月平均增长率;(2)、从4月份起,商场决定采用降价促销的方式回馈顾客,经试验,发现该款徽章每降价1元,月销售量就会增加20枚,当该款徽章降价多少元时,月销售利润达8400元?
-
4、爱乐实水果超市以每箱元的价格从水果批发市场购进箱橘子,若以每箱净重为标准,超过的千克数记为正数,不足的千克数记为负数,称重的记录如下表:
与标准质量的差值/kg
0
箱数
3
3
7
5
2
(1)、这箱橘子的总质量是多少?(2)、需要将橘子从批发市场送到水果超市,现有两种取货方式:方式一:批发市场送货上门,需另交元送货费;
方式二:超市雇车自取,需支付租车费和装卸费:
租车费:元
装卸费:以内(包括)元, 超出的部分元 .
请你根据计算说明超市应选择哪种取货方式,并求出箱橘子的成本.
(3)、在(2)的条件下,若水果店按获利计算出零售价,并以零售价售出一部分收回成本后,剩余的橘子全部七折销售,请计算该水果店在销售这批橘子过程中共盈利多少元?(利润率) -
5、如图所示,四个规格相同的正方形网格,按下列要求画格点正方形(4个顶点均在格点的正方形).
 (1)、在图1中画出与图甲中阴影部分面积相等的正方形.(2)、在图2中画出与图乙中阴影部分面积相等的正方形.
(1)、在图1中画出与图甲中阴影部分面积相等的正方形.(2)、在图2中画出与图乙中阴影部分面积相等的正方形. -
6、计算:(1)、(2)、(3)、(4)、
-
7、有下列各数:① , ②;③;④0;⑤;⑥;⑦(每两个3之间依次多一个1).(1)、属于整数的有________.(填序号)(2)、属于负分数的有________(填序号)(3)、属于无理数的有________(填序号)
-
8、如图,在数轴上表示出下列各数: , , 0, , 并用“<”把这些数连接起来.

______<______<______<______
-
9、若 , 其中均是整数,则 .
-
10、若a,b互为倒数,c,d互为相反数,m的绝对值是3,则的值是( )A、或11 B、7或11 C、或 D、7或11(D和B重复了)
-
11、如图,数轴上的点E,F,M,N表示的实数分别为﹣2,2,x,y,下列四个式子中结果一定为负数是( )
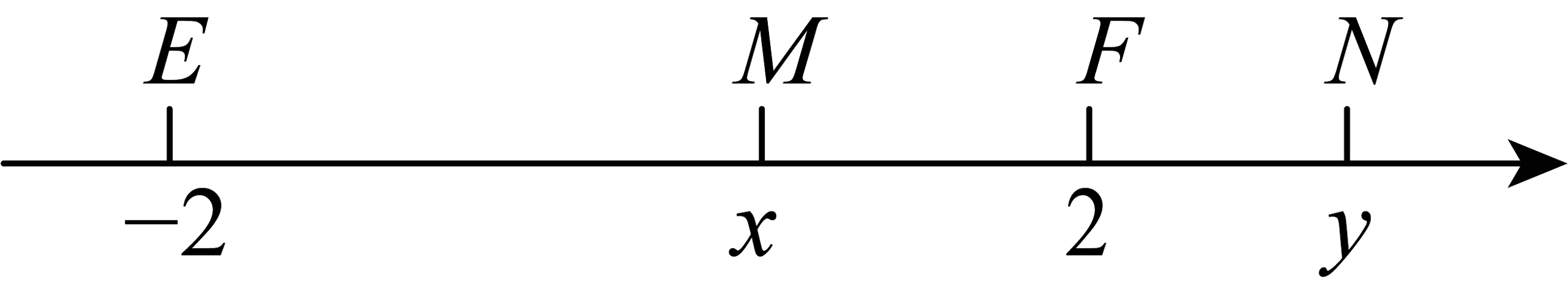 A、x+y B、2+y C、x﹣2 D、2+x
A、x+y B、2+y C、x﹣2 D、2+x -
12、如图,在中, , 是边上的一点, , , .
 (1)、判断的形状,并说明理由;(2)、求的周长.
(1)、判断的形状,并说明理由;(2)、求的周长. -
13、如图,在中, , 点P在上运动,点D在上运动,始终保持与相等,的垂直平分线交于点E,交于点F,连接 .
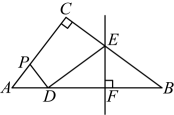 (1)、判断与的位置关系,并说明理由;(2)、若 , , , 求线段的长.
(1)、判断与的位置关系,并说明理由;(2)、若 , , , 求线段的长. -
14、如图,在中, , 垂足为D, , 垂足为E,与相交于点F,已知 .
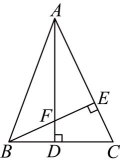 (1)、求证:;(2)、若 , , 求的长.
(1)、求证:;(2)、若 , , 求的长. -
15、菊花作为“花中四君子”之一,象征着高雅和刚正不阿的品质,尤其在秋寒时节盛开,象征着坚韧不拔的精神.第十三届国际菊花展于2024年10月15日在河南开封清明上河园举办.本届菊花展有近800个菊花品种参展.为增进学生对菊花及其文化的了解,学校欲购进一批菊花盆栽放置在如图所示的区域供同学们观赏.已知 , , , , . 求放置菊花盆栽区域的面积.
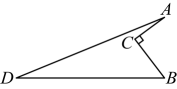
-
16、如图,在修一条东西走向的公路时遇到一座小山,于是要修一条隧道 . 已知、、三点在同一条直线上.为了在小山的两侧、同时施工,过点作一条南北走向的直线l(即直线l , 在直线l上取一点 , 使得米,经测量米.若施工队每天共挖米,求施工队几天能挖完?
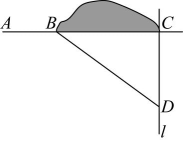
-
17、如图,甲乙两船从港口P同时出发,甲船以16海里/小时的速度向北偏东航行,乙船向南偏东航行.3小时后,甲船到达A岛,乙船到达B岛.若A、B两岛相距60海里,问:乙船的航速是多少?
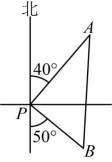
-
18、学生安全是近几年社会关注的重大问题,其中交通安全隐患主要是超速.如图,某校门前一条直线公路建成通车,在该路段限速 , 为了检测车辆是否超速,在公路旁设立了观测点C,从观点C测得一小车从点A到达点B行驶了 . 若测得 , , . 此车超速了吗?请说明理由.( , )
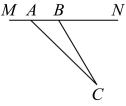
-
19、如图,在中,于点D, , , .
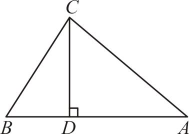 (1)、求的长;(2)、求的长;
(1)、求的长;(2)、求的长; -
20、若是的三边,且 , 则的面积为 .