-
1、多项式 是次项式,它的最高次项的系数是.
-
2、用长度相同的木棍按如图所示的规律拼图案,其中图案①用了9根木棍,图案②用了14根木棍,图案③用了19根木棍,图案④用了24 根木棍……按此规律排列下去,则图案⑧用的木棍根数是( )
 A、39 B、44 C、49 D、54
A、39 B、44 C、49 D、54 -
3、下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面:
 +y2 , 阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的部分应是( ) A、 B、 C、 D、
+y2 , 阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的部分应是( ) A、 B、 C、 D、 -
4、如图,为制作一个试管架,在长为a cm的木板上钻3个小孔,每个小孔的直径都是2cm,则x等于( ) cm.
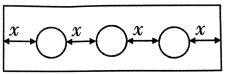 A、 B、 C、 D、
A、 B、 C、 D、 -
5、若当 时,代数式 的值是1024,则当-1时,代数式 的值是( )A、-1020 B、-1021 C、-1022 D、1021
-
6、若多项式 与 相加后,不含二次项,则常数的值是( )A、2 B、-3 C、-2 D、-8
-
7、下列去括号错误的是( )A、 B、 C、 D、
-
8、如果单项式 与 是同类项,那么a,b的值分别为( )A、2,4 B、2,3 C、3,4 D、3,3
-
9、下列说法中正确的是( )A、不是整式 B、的次数是4 C、与是同类项 D、是单项式
-
10、下列代数式: 0.整式有( )A、3个 B、4个 C、5个 D、6个
-
11、下列各式符合代数式书写规范的是( )A、 B、 C、元 D、
-
12、某县对辖区内部分初中学生就“每天完成书面作业的时间”进行了随机调查,为便于统计学生每天完成书面作业的时间(用t表示,单位:h)状况,设置了四个选项,分别为A:t≤1,B:1<t≤1.5,
C:1.5<t≤2,D:t>2,并根据调查结果绘制了两幅不完整的统计图.


请根据以上提供的信息解答下列问题:
(1)、此次调查,选择选项A的学生人数是多少?(2)、在扇形统计图中,选项D所对应的扇形圆心角的度数为多少?(3)、如果该县有15 000名初中学生,那么请估算该县“每天完成书面作业的时间不超过90 min”的初中学生人数.(4)、请回答你每天完成书面作业的时间属于哪个选项,并对老师的书面作业布置提出合理化建议. -
13、某校为了解九年级学生对自己三年来所用的数学课本的看法,对120名同学进行问卷调查,并得到下表:
意见
非常喜欢
喜欢
有一点喜欢
不喜欢
人数
48
45
24
3
(1)、分别计算每一种意见的人数占调查人数的百分比;(2)、根据上述统计表中的数据分别画出折线统计图和扇形统计图. -
14、有效的垃圾分类,可以减少污染,保护地球上的资源.为了更好地开展垃圾分类工作,某社区居委会对本社区居民掌握垃圾分类知识的情况进行调查.从中随机抽取部分居民进行垃圾分类知识测试,测试结果分为A,B,C,D四个等级,绘制成如图所示的两幅不完整的统计图.
 (1)、求测试结果为D等级的人数占调查总人数的百分比;(2)、在扇形统计图中,求表示D等级的扇形的圆心角的度数;(3)、测试结果为A等级的有多少人?并补全条形统计图.
(1)、求测试结果为D等级的人数占调查总人数的百分比;(2)、在扇形统计图中,求表示D等级的扇形的圆心角的度数;(3)、测试结果为A等级的有多少人?并补全条形统计图. -
15、李老师调查了班上50名学生上学路上所花的时间,他发现学生所花时间都少于50 min,然后将调查数据整理,作出如图所示的频数直方图的一部分(每组包括前一个端点值,不包括后一个端点值).
 (1)、补全频数直方图;(2)、该班学生在路上花费的时间在哪个范围内最多?(3)、该班学生上学路上花费时间在30 min以上(含30 min)的人数占全班人数的百分比是多少?
(1)、补全频数直方图;(2)、该班学生在路上花费的时间在哪个范围内最多?(3)、该班学生上学路上花费时间在30 min以上(含30 min)的人数占全班人数的百分比是多少? -
16、小雨同学为调查一个月内全校1 000名学生的借书情况,在校园里对学生进行调查,并绘制了如下表格:
借书次数
0
1
2
3
4及4以上
学生人数
45
33
15
5
2
(1)、小雨同学采用的是什么调查方式?(2)、总体、个体、样本各是什么? -
17、某中学六年级甲、乙两个班参加了一次数学考试,考试人数每班都为40人,每个班的考试成绩分为A,B,C,D,E五个等级,绘制的统计图如图所示.根据统计图提供的信息,知D等级这一组人数较多的班是.
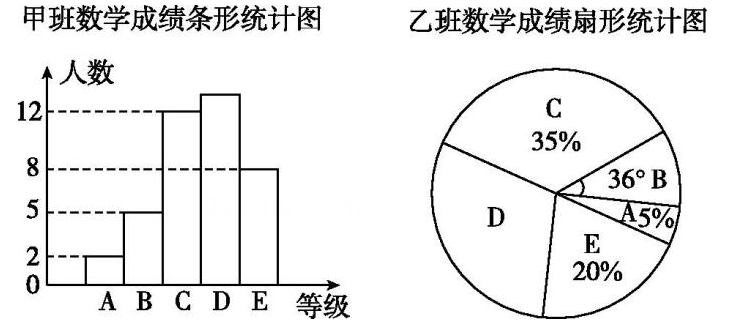
-
18、如图所示是一、二两组同学根据本组最近5次数学平均成绩分别绘制成的折线统计图.由统计图可知组进步更大.(选填“一”或“二”)

-
19、小明调查了本班每位同学课外阅读的喜好,并绘制了如图所示不完整的扇形图和条形图(柱的高度从高到低排列).条形图不小心被撕了一块,图中括号内应填的种类是.

-
20、某校举行“大赞美丽家乡,我为家乡代言”活动,同学们积极参加.如图所示是七(1)班同学6月份连续7天投稿数量的折线统计图,则稿件数量不少于5篇的共有天.
