-
1、下面各式去括号正确的是( )A、x2-(3x-2)=x2-3x-2 B、7a+(5b-1)=7a+5b+1 C、2m2-(3m+5)=2m2-3m-5 D、-(a-b)+(ab-1)=a-b+ab-1
-
2、按一定规律排列的代数式:2x,3x2 , 4x3 , 5x4 , 6x5 , …,第n个代数式是( )A、2xn B、(n-1)xn C、n D、(n+1)xn
-
3、对甲、乙同学关于“代数式10a+b”的意义的叙述,判断正确的是( )
甲:a与b的和的10倍;
乙:若a和b分别表示一个两位数中的十位数字和个位数字,则10a+b表示这个两位数.
A、只有甲正确 B、只有乙正确 C、甲、乙都正确 D、甲、乙都不正确 -
4、下列叙述正确的是( )A、1÷a是整式 B、x2+x2y-2yx2+1是二次四项式 C、的各项系数都是 D、-x3+2x2-1的常数项是-1
-
5、计算2a2-a2的结果是( )A、2 B、a2 C、3a2 D、2a4
-
6、将连续的偶数2,4,6,8,10,…排成如下的数表.
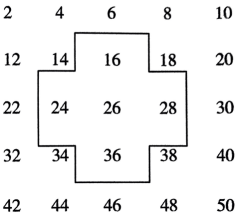 (1)、十字框中五个数的和与中间的数26有什么关系?(2)、设中间的数为m,用代数式表示十字框中的五个数的和.(3)、十字框中的五个数之和能等于2060吗? 若能,请写出这五个数;若不能,请说明理由.
(1)、十字框中五个数的和与中间的数26有什么关系?(2)、设中间的数为m,用代数式表示十字框中的五个数的和.(3)、十字框中的五个数之和能等于2060吗? 若能,请写出这五个数;若不能,请说明理由. -
7、三个队植树,第一队植树a棵,第二队植的树比第一队的2倍还多6棵,第三队植的树比第二队的一半少3棵.(1)、三个队共植树多少棵?(用含 a 的代数式表示)(2)、当a=50时,求三个队共植树多少棵.
-
8、商店进了一批货,出售时要在进价的基础上加上一定的利润,其质量x(千克)与售价y(元)之间的关系如下表.
质量x/千克
1
2
3
4
…
售价y/元
5.5+0.7
11+1.4
16.5+2.1
22+2.8
…
(1)、用含x的代数式表示售价y.(2)、当 时,求y的值. -
9、先化简,再求值.(1)、其中(2)、其中
-
10、化简.(1)、(2)、(3)、(4)、
-
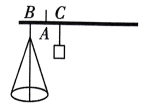
11、如图是某种杆秤的示意图.在秤杆的点 A 处固定提纽,点B 处挂秤盘,点C 为0刻度点.当秤盘不放物品时,提起提纽,秤砣所挂位置移动到点C,秤杆处于平衡.秤盘放入x克物品后移动秤砣,当秤砣所挂位置与提纽的距离为 y 毫米时秤杆处于平衡状态.测得x 与y的几组对应数据如下表.
x/克
0
2
4
6
10
y/毫米
10
14
18
22
30
由表中数据的规律可知,当克时,毫米.
-
12、已知多项式中不含字母y,则a 的值为.
-
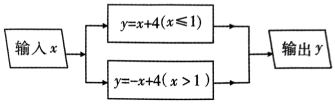
13、根据如图所示的程序,当输入 时,输出的结果.
-
14、如果 与 的和是一个单项式,那么的值为.
-
15、在一次植树活动中,某班有a 名男生,每人植树 3 棵,有b名女生,每人植树2 棵,则该班同学一共植树棵. (用含a,b的代数式表示)
-
16、多项式 是次项式,它的最高次项的系数是.
-
17、用长度相同的木棍按如图所示的规律拼图案,其中图案①用了9根木棍,图案②用了14根木棍,图案③用了19根木棍,图案④用了24 根木棍……按此规律排列下去,则图案⑧用的木棍根数是( )
 A、39 B、44 C、49 D、54
A、39 B、44 C、49 D、54 -
18、下面是小芳做的一道多项式的加减运算题,但她不小心把一滴墨水滴在了上面:
 +y2 , 阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的部分应是( ) A、 B、 C、 D、
+y2 , 阴影部分即为被墨汁弄污的部分,那么被墨汁遮住的部分应是( ) A、 B、 C、 D、 -
19、如图,为制作一个试管架,在长为a cm的木板上钻3个小孔,每个小孔的直径都是2cm,则x等于( ) cm.
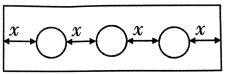 A、 B、 C、 D、
A、 B、 C、 D、 -
20、若当 时,代数式 的值是1024,则当-1时,代数式 的值是( )A、-1020 B、-1021 C、-1022 D、1021