-
1、已知二次函数 , 当 时, , 时,.(1)、 求 a,c 的值;(2)、 当 时,求函数 y 的值.
-
2、已知 是关于 x 的二次函数. 求 m 的值及函数表达式.
-
3、 二次函数 , 当 时,对于每一个 x 的值, 始终成立,则 a 的取值范围是.
-
4、 如图,在相距 2m 的两棵树上拴了一根绳子做成一个简易秋千,拴绳子的地方都高出地面 2.6m,绳子自然下垂近似呈抛物线形,当身高 1.1m 的小妹距较近的那棵树 0.5m 时,头部刚好接触到绳子,则绳子的最低点距地面的距离为m.

-
5、 已知抛物线 经过点 (1,1),则代数式 的值为.
-
6、 若抛物线 经过 和 两点,则 .
-
7、 已知点 , 在抛物线(k 为常数)上,则 , 的大小关系是.
-
8、 请写出一个开口向上,对称轴为y轴的抛物线的表达式:.
-
9、 已知函数的图象如图所示,若直线与该图象有公共点,则k的最大值与最小值的和为( )
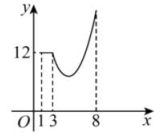 A、2 B、12 C、15 D、17
A、2 B、12 C、15 D、17 -
10、 已知二次函数的图象如图所示,有下列4个结论,其中正确的结论是( )
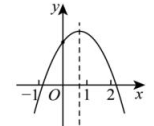 A、 B、 C、 D、
A、 B、 C、 D、 -
11、 如图所示,二次函数与反比例函数的图象大致是( )A、
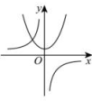 B、
B、 C、
C、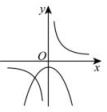 D、
D、
-
12、 某湖面上有一座抛物线形拱桥,按如图所示的方式建立平面直角坐标系,得到抛物线的函数解析式为 , 正常水位时,水面宽 AB 为 16m,此时拱顶 O 到水面 AB 的距离为( )
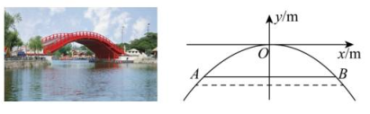 A、4m B、3m C、2m D、1m
A、4m B、3m C、2m D、1m -
13、 已知二次函数的图象如下图所示,关于该函数在所给自变量取值范围内,下列说法中正确的是( )
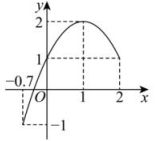 A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值
A、有最小值0,有最大值2 B、有最小值-1,有最大值0 C、有最小值-1,有最大值2 D、有最小值-1,无最大值 -
14、 将二次函数 的图象向右平移 1 个单位,再向下平移 2 个单位后,所得抛物线为( )A、 B、 C、 D、
-
15、 抛物线 的顶点在( )A、y轴上 B、x轴上 C、原点 D、第二象限
-
16、 二次函数的图象的对称轴是( )A、直线 B、直线 C、直线 D、直线
-
17、 下列函数中是二次函数的是( )A、 B、 C、 D、
-
18、阅读下列材料并解答问题:
在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”.
例如:一个三角形三个内角的度数分别是 , , , 这个三角形就是一个“3倍角三角形”.反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.
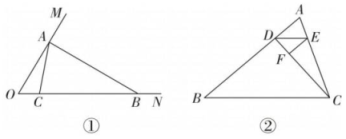 (1)、如图①,已知 , 在射线OM上取一点A,过点A作交ON于点B,判断△AOB是不是“3倍角三角形”,为什么?(2)、在(1)的条件下,以A为端点画射线AC,交线段OB于点C(点C不与点O、点B重合),若△AOC是“3倍角三角形",求∠ACB的度数;(3)、如图②,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得 , , 若△BCD是“3倍角三角形”,求∠B的度数.
(1)、如图①,已知 , 在射线OM上取一点A,过点A作交ON于点B,判断△AOB是不是“3倍角三角形”,为什么?(2)、在(1)的条件下,以A为端点画射线AC,交线段OB于点C(点C不与点O、点B重合),若△AOC是“3倍角三角形",求∠ACB的度数;(3)、如图②,点D在△ABC的边上,连接DC,作∠ADC的平分线交AC于点E,在DC上取一点F,使得 , , 若△BCD是“3倍角三角形”,求∠B的度数. -
19、 综合与实践:三角形的中线把三角形分成面积相等的两部分.
已知:如图1,在中,点D是BC边上的中点,连接AD. 则:.
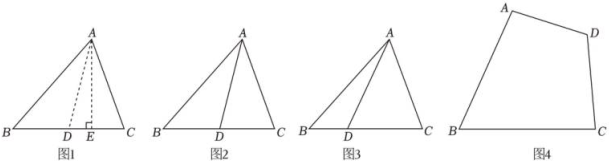 (1)、如图2,在中,点D是BC边上的中点,若 , ;(2)、如图3,在中,点D是BC边上的点且 , 和存在怎样的数量关系?请模仿写出证明过程;(3)、现在有一块四边形土地ABCD(如图4),熊大和熊二都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.
(1)、如图2,在中,点D是BC边上的中点,若 , ;(2)、如图3,在中,点D是BC边上的点且 , 和存在怎样的数量关系?请模仿写出证明过程;(3)、现在有一块四边形土地ABCD(如图4),熊大和熊二都想问老熊要这块地,老熊让他们平分,可他们谁都没法平分,请你来帮帮忙.要求:用不超过三条的线段画出平分方法,并对作法进行描述. 可利用带刻度的直尺.
-
20、 如图,在中,的延长线于E,的延长线于F,M为BC的中点,分别连接ME、MF、EF.
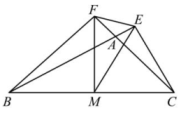 (1)、 若 , , 求的周长;(2)、 若 , , 求的度数.
(1)、 若 , , 求的周长;(2)、 若 , , 求的度数.