-
1、 如图,CD平分 , .
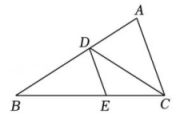 (1)、 判断DE与AC的位置关系,并说明理由;(2)、 若 , 求的度数.
(1)、 判断DE与AC的位置关系,并说明理由;(2)、 若 , 求的度数. -
2、(1)、 已知 , , 求 ab 与 的值;(2)、 已知 的三边分别是 a, b, c,化简代数式:.
-
3、 如图, , , 且. 若 , 求的度数.

-
4、 已知:如图我们把它称为“8字形”,试说明:.

-
5、 如图是一块矩形菜地ABCD,宽米,长米,面积为平方米. 现将边AB增加1米.
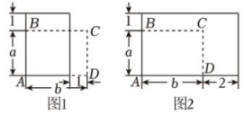 (1)、如图1,若 , 边AD减少1米,得到的矩形面积不变,则的值是.(2)、如图2,若边AD增加2米,得到的矩形面积为2s平方米,且 , 为正整数,则的值是.
(1)、如图1,若 , 边AD减少1米,得到的矩形面积不变,则的值是.(2)、如图2,若边AD增加2米,得到的矩形面积为2s平方米,且 , 为正整数,则的值是. -
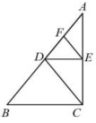
6、 如图,CD是的中线,DE是的中线,EF是的中线,若的面积为 , 则的面积为.
-
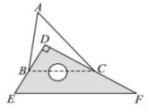
7、 如图,将一块直角三角板 DEF 放置在锐角 上,使得该三角板的两条直角边 DE, DF 恰好分别经过点 B, C. 若 时,点 D 在 内,则 的值是.
-
8、 如图,三角形纸片ABC中, , , 将沿DE对折,使点C落在外的点C'处,若 , 则的度数为.
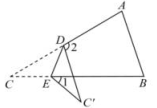
-
9、 如图,在中, , , 则的度数是.
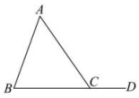
-
10、 如图,在中,和的平分线AE,BF相交于O,AE交BC于E,BF交AC于F,过点F作于D,下列结论中:①;②当时,;③;④若 , , 则 , 正确的是( )
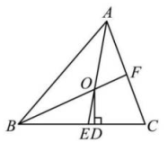 A、①②③ B、②③④ C、①③④ D、①②④
A、①②③ B、②③④ C、①③④ D、①②④ -
11、 如图,点 D 是 边 BC 上的中点,点 E 是 AD 上一点且 DE = 3AE,F、G 是边 AB 上的三等分点,若四边形 FGDE 的面积为 14,则 的面积是( )
 A、24 B、42 C、48 D、56
A、24 B、42 C、48 D、56 -
12、 如图,在中, , 按图进行翻折,使 , , 则的度数是( )
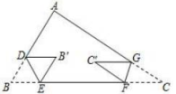 A、 B、 C、 D、
A、 B、 C、 D、 -
13、 如图,在中, , , D是BC边上的一点,若的周长比的周长大2,则AD是( )
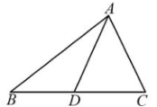 A、的高 B、的角平分线 C、的中线 D、都有可能
A、的高 B、的角平分线 C、的中线 D、都有可能 -
14、 下列命题中,是真命题的是( )A、相等的角是对顶角 B、内错角相等,两直线平行 C、同旁内角互补 D、若 , 则
-
15、 某品牌手机自主研发了最新型号芯片,其晶体管栅极的宽度为0.00000007毫米,将数据0.00000007用科学记数法表示为( )A、 B、 C、 D、
-
16、已知抛物线 (a,b 为常数,且 )。(1)、 当 , 时,直接写出顶点坐标;当 , 时,直接写出顶点坐标;(2)、 抛物线的顶点坐标随 a、b 的取值而改变,若 , 当抛物线的顶点在最低位置时:
① 求 a 与 b 满足的关系式;
② 抛物线上有两点 (2,s),(m,t),当 时,求 m 的取值范围.
-
17、在一次高尔夫球的练习中,小成在 O 处击球,其飞行路线满足抛物线 . 其中 y(m) 是球的飞行高度,x(m) 是球飞出的水平距离,结果球离球洞的水平距离还有 2m.
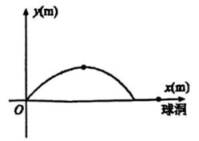 (1)、 请求出抛物线的顶点坐标;(2)、 请求出球洞离击球点的距离;(3)、 若小成再一次从 O 处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线?求出其解析式.
(1)、 请求出抛物线的顶点坐标;(2)、 请求出球洞离击球点的距离;(3)、 若小成再一次从 O 处击球,要想让球飞行的最大高度不变且球刚好进洞,则球飞行路线应满足怎样的抛物线?求出其解析式. -
18、如图,用长为 40cm 的细铁丝围成一个矩形 ABCD(),若这个矩形为黄金矩形(AD 与 AB 之比等于黄金比).
 (1)、 求该矩形的长.(结果保留根号)(2)、 求该矩形的面积.(结果保留根号)
(1)、 求该矩形的长.(结果保留根号)(2)、 求该矩形的面积.(结果保留根号) -
19、口袋里只有8个球,除颜色外都相同. 其中有x个红球,y个白球,没有其他颜色的球,从中任意摸出一个球:(1)、如果摸到红球与摸到白球的可能性相等,分别求x和y的值;(2)、在(1)的条件下,现从布袋中取出若干个白球,并放入相同数量的红球,搅拌均匀后,再从口袋中摸出一个球是红球的概率是 , 求取走了多少个白球.
-
20、一个斜抛物体的水平运动距离记为x(m),对应高度记为h(m),h与x之间具有函数关系(a,b是常数,).已知当时,;当时,.(1)、 求h关于x的函数表达式.(2)、 求斜抛物体的最大高度和达到最大高度时的水平运动距离