相关试卷

1、计算：

(1)、 $(- 12) - 5 + (- 14) - (- 39)$ ；

(2)、 $(1 \frac{3}{4} - \frac{7}{8} - \frac{7}{12}) \times (- \frac{8}{7})$

(3)、 $(- \frac{3}{4}) \times (- \frac{1}{2}) + (- 1 \frac{1}{8}) \times 3$

(4)、 $- 2^{3} + [{(- 4)}^{2} - (1 - 3^{2}) \times 3]$ ；

查看解析
2、如图所示的程序框图，如图所示的运算程序中，若开始输入的 $x$ 值为100，我们发现第1次输出的结果为50，第2次输出的结果为25，…，第2025次输出的结果为．

查看解析
3、对任意有理数 $x$ 、 $y$ 定义新运算“ $\oplus$ ”如下： $x \oplus y = x^{2} - y$ ．则 $(- 2) \oplus 3 =$ ．

查看解析
4、某班有女生a人，男生比女生的2倍少5人，则男生有人．

查看解析
5、在数轴上，点A表示的数是 $- 3$ ，与A距离3个单位长度的点表示的数是．

查看解析
6、当前手机微信支付已经成为一种新型的支付方式，倍受广大消费者的青睐．如果微信零钱收入22元记为 $+ 22$ 元，那么微信零钱支出18元记为元．

查看解析
7、下列说法正确的是（）

A、 $- \frac{2 x^{2} y}{3}$ 的系数是 $- 2$ B、 $- \frac{3 π x^{2} y^{3}}{5}$ 的次数是6 C、多项式 $2 x^{3} - 4 x - 1$ 的常数项是1 D、多项式 $x^{2} + 2 x + 1$ 是二次三项式

查看解析
8、点a在数轴上的位置如图所示，试比较a、 $\frac{1}{a}$ 、 $|a|$ 大小关系正确的是（　　）

A、 $a < \frac{1}{a} \leq |a|$ B、 $\frac{1}{a} < a < |a|$ C、 $a < |a| < \frac{1}{a}$ D、 $|a| \leq a \leq \frac{1}{a}$

查看解析
9、已知4个有理数： $- 1^{2020}$ ， $|- 2|$ ， $- (- 1.5)$ ， ${(- 3)}^{2}$ ，其中正数的个数是（　　）

A、1 B、2 C、3 D、4

查看解析
10、单项式 $9 x^{m} y^{3}$ 与单项式 $4 x^{2} y^{n}$ 是同类项，则 $- m n$ 的值是（）

A、 $- 5$ B、 $- 6$ C、5 D、6

查看解析
11、 $A B = 16 cm$ ， $A C = 12 cm$ ，动点P、Q分别以每秒 $2 cm$ 和 $1 cm$ 的速度同时开始运动，其中点P从点A出发沿 $A C$ 边一直移到点C为止，点Q从点B出发沿 $B A$ 边一直移动到点A为止．

(1)、写出 $A P$ 的长 $y_{1}$ 和 $A Q$ 的长 $y_{2}$ 关于时间t的函数；

(2)、经过多少时间后， $△ A P Q$ 与 $△ A B C$ 相似？

(3)、在整个过程中，是否存在使 $△ A P Q$ 的面积恰好为 $△ A B C$ 面积一半的情况，若存在，请问此时点Q运动了多少时间？若不存在，请说明理由．

查看解析
12、如图，在△ABC中，D、F分别是BC、AC边的中点，连接DA、DF，且AD＝2DF，过点B作AD的平行线交FD的延长线于点E．
（1）求证：四边形ABED为菱形；
（2）若BD＝6，∠E＝60°，求四边形ABEF的面积．

查看解析
13、如图，晚上，小亮在广场上乘凉．图中线段AB表示站在广场上的小亮，线段PO表示直立在广场上的灯杆，点P表示照明灯．
（1）请你在图中画出小亮在照明灯（P）照射下的影子；
（2）如果灯杆高PO＝12m，小亮的身高AB＝1.6m，小亮与灯杆的距离BO＝13m，请求出小亮影子的长度．

查看解析
14、用适当的方法解下列方程．

(1)、 ${(2 x + 3)}^{2} - 16 = 0$ ；

(2)、 ${(2 x + 1)}^{2} = 3 (2 x + 1)$ ；

(3)、 $x^{2} - 2 x - 5 = 0$ ；

(4)、 $x^{2} - 6 x - 27 = 0$ ．

查看解析
15、如图，在平行四边形 $A B C D$ 中，已知 $A D = 8$ ， $A B = 6$ ， $D E$ 平分 $∠ A D C$ 交 $B C$ 边于点 $E$ ，则 $B E$ 等于．

查看解析
16、某数学兴趣小组来到城关区时代广场，设计用手电来测量广场附近某大厦CD的高度，如图，点P处放一水平的平面镜．光线从点A出发经平面镜反射后刚好射到大厦CD的顶端C处，已知AB⊥BD，CD⊥BD，测得AB＝1.5米，BP＝2米，PD＝52米，那么该大厦的高度约为（　　）

A、39米 B、30米 C、24米 D、15米

查看解析
17、有四张不透明的卡片，正面分别标有数字0、1、2、3．除正面的数字不同外，其余都相同．将它们背面朝上洗匀后，从中随机抽取一张，抽到写有偶数卡片的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{4}$ D、 $\frac{3}{4}$

查看解析
18、小明从正面如图所示的两个物体，看到的是平面图形中的（）

A、 B、 C、 D、

查看解析
19、如图1，点D是△ABC中AB边上一点，∠ACD＝∠B， BC²＝AB·BD．

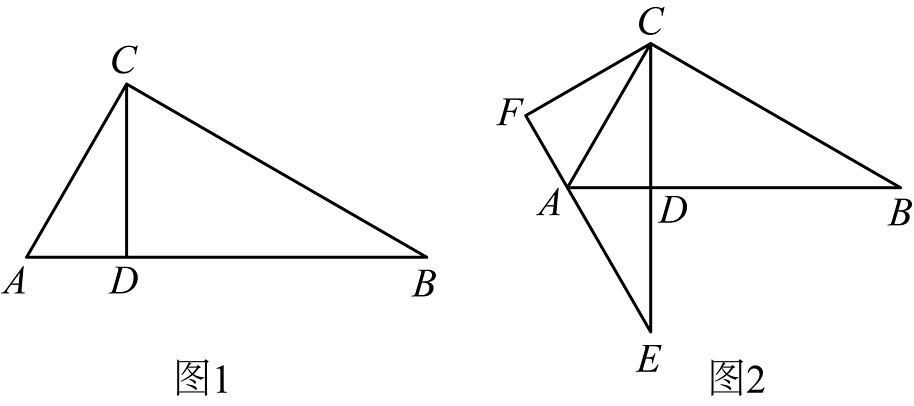(1)、求证：∠ADC＝∠ACB；

(2)、求∠ACB的度数；

(3)、将图1中的△BCD绕点C顺时针旋转得到△ECF，BD的对应边EF经过点A(如图2所示)，若AC＝2，求线段CD的长．

查看解析
20、如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 6 cm$ ， $B C = 12 cm$ ，动点P从点A开始沿着边 $A B$ 向点B以 $1 cm/s$ 的速度移动（不与点B重合），动点Q从点B开始沿着边 $B C$ 向点C以 $2 cm/s$ 的速度移动（不与点C重合）．若P、Q两点同时移动 $t (s)$ ；

(1)、当运动几秒时， $△ B P Q$ 的面积为 $9 {cm}^{2}$ ．

(2)、若 $P Q$ 两点同时分别从A、B出发，经过多长时间 $△ A B C$ 与 $△ B P Q$ 相似？

查看解析

上一页 876 877 878 879 880 下一页跳转