-
1、二次函数的图象与轴交于 , 两点,若 , 且 , 记 , 则( )A、有最小值 , 没有最大值 B、有最小值 , 没有最大值 C、有最小值 , 有最大值4 D、有最小值 , 有最大值4
-
2、如图,大半圆中有个大小不同的小半圆,所有小半圆的直径和等于大半圆的直径.大半圆弧长为 , 个小半圆的弧长和为 , 则( )
 A、 B、 C、 D、无法确定
A、 B、 C、 D、无法确定 -
3、已知点 , , 在抛物线的图象上,则( )A、 B、 C、 D、
-
4、如图,将绕顶点A逆时针旋转得到 . 若点恰好落在边上,且 , 则旋转角的大小是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
5、在平面直角坐标系中,把抛物线先向右平移2个单位长度,再向上平移1个单位长度,平移后抛物线的解析式为( )A、 B、 C、 D、
-
6、如图,直线与半径为的相交,且点到直线的距离为7,则的值可以是( )
 A、3 B、4 C、7 D、10
A、3 B、4 C、7 D、10 -
7、用配方法解一元二次方程时可配方得( )A、 B、 C、 D、
-
8、如图,在平面直角坐标系中,直线分别与轴、轴交于点、 .
 (1)、求直线的解析式;(2)、求;(3)、若点C在轴上且为等腰三角形,请直接写出所有满足条件的点的坐标.
(1)、求直线的解析式;(2)、求;(3)、若点C在轴上且为等腰三角形,请直接写出所有满足条件的点的坐标. -
9、汽车油箱中有汽油 , 如果不再加油,那么油箱中的油量(单位)随行驶里程(单位:)的增加而减少,平均耗油量为 .(1)、写出表示与的函数解析式(直接写出自变量的取值范围);(2)、当汽车行驶时,油箱中还有多少升()油?(3)、若汽车要行驶 , 那么油箱中的油是否够用?若不够用,中途还需加多少升汽油?
-
10、如图所示,在直角坐标系中, .
 (1)、作出关于轴的对称图形;(2)、写出的顶点坐标;(3)、求出的面积.
(1)、作出关于轴的对称图形;(2)、写出的顶点坐标;(3)、求出的面积. -
11、计算下列各式:(1)、(2)、(3)、
-
12、小明在数轴上先作边长为1的正方形,再用圆规画出了点A(如图所示),则点A所表示的数为 .

-
13、某校有4名教师与若干名学生去看电影,电影票原价为成人每张30元,学生每张15元.现全部打8折.则打折后付款总金额y(元)与学生人数x(人)之间的函数关系式为 .
-
14、若<0,则在平面直角坐标系中,点在第象限.
-
15、若点在一次函数的图象上,则的大小关系是( )A、 B、 C、 D、
-
16、如图,一次函数与x轴的交点为P,则关于x的一元一次方程的解为( )
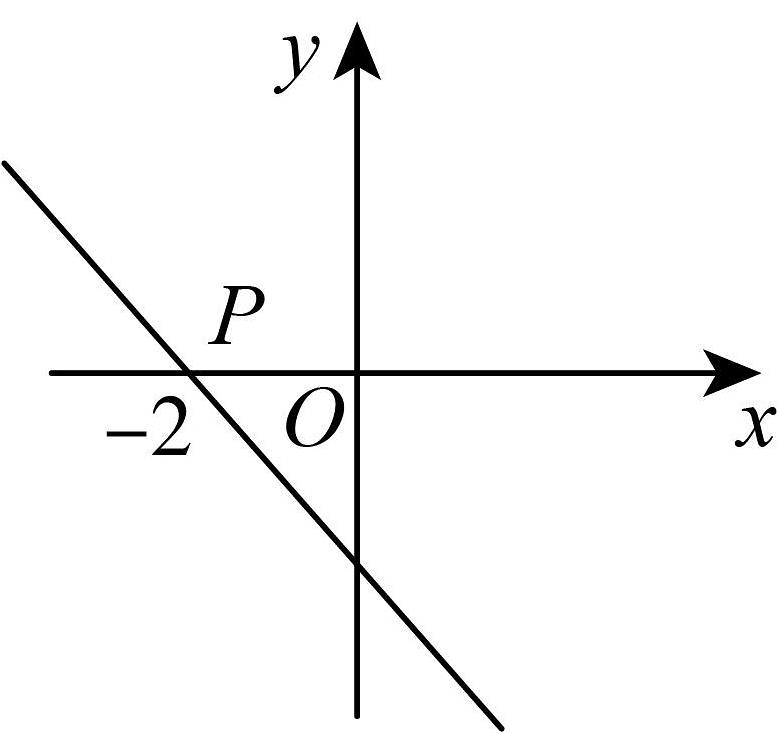 A、-2 B、2 C、3 D、-1
A、-2 B、2 C、3 D、-1 -
17、正比例函数的函数值y随着x增大而增大,则一次函数的图象大致是( )A、
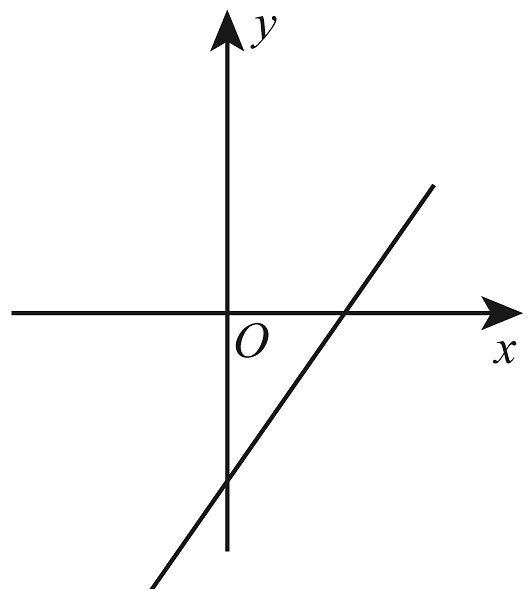 B、
B、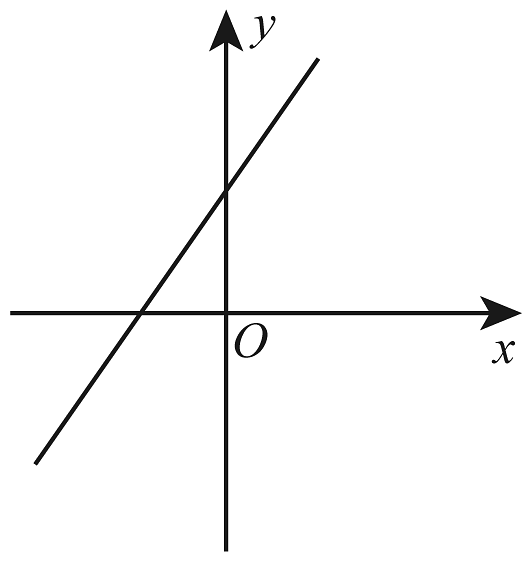 C、
C、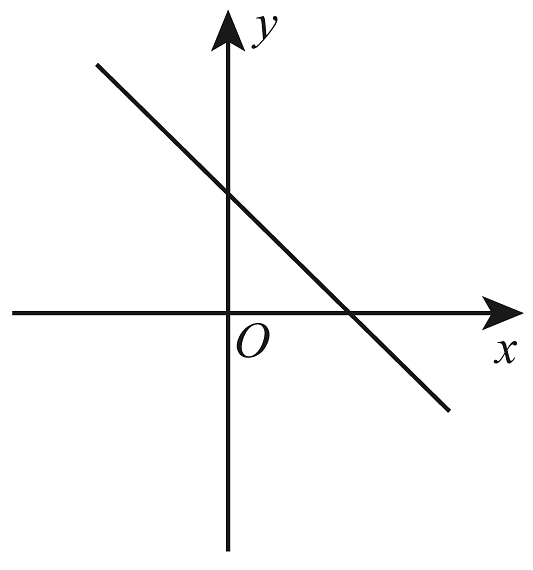 D、
D、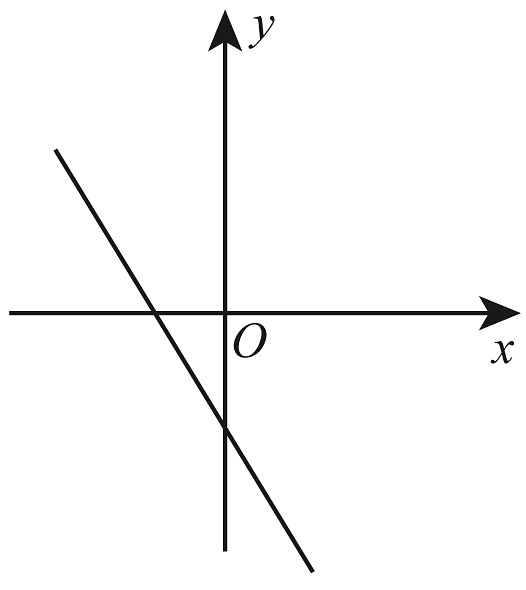
-
18、如图,部分围棋棋盘在某平面直角坐标系内,黑棋(甲)的坐标为 , 则白棋(甲)的坐标为( )
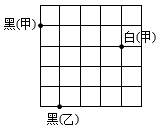 A、 B、 C、 D、
A、 B、 C、 D、 -
19、以下列三个数为边长的三角形中,能构成直角三角形的是( )A、1,2,3 B、2,3,4 C、6,8,10 D、9,16,25
-
20、如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴相交于点 , 与轴交于点 , 与正比例函数的图象相交于点 , 点的横坐标为1.
 (1)、求一次函数的函数解析式;(2)、不等式的解集是________;(3)、为直线上一点,过点作轴的平行线交于点 , 当时,求点的坐标.
(1)、求一次函数的函数解析式;(2)、不等式的解集是________;(3)、为直线上一点,过点作轴的平行线交于点 , 当时,求点的坐标.