-
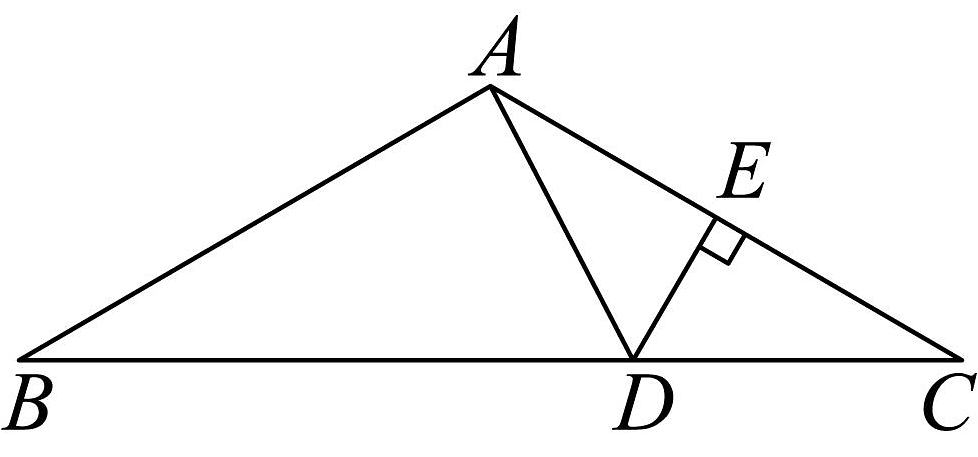
1、如图,在中, , , 的垂直平分线交于点E,交于点D,则的度数是 .
-
2、若是完全平方式,则 .
-
3、使式子有意义的的取值范围是 .
-
4、已知的立方根是 , 则 .
-
5、下列运算错误的是( )A、 B、 C、 D、
-
6、下列二次根式中是最简二次根式的是( )A、 B、 C、 D、
-
7、如图,已知数轴上点A表示的数为6,且AB=10,动点P从点A出发,以每秒2个单位长度的速度沿数轴向左匀速运动,设运动时间为t秒(t>0).

(1)数轴上点B表示的数为 , 当t=2时,点P表示的数为 ;
(2)动点R从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问经过多长时间P,R两点相遇?
(3)动点R从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,若点P,R同时出发,问点R运动多长时间P,R两点相距2个单位长度?
-
8、阅读材料:我们知道, . 类似的,我们把看成一个整体,则 . “整体思想”是中学教学解题中的一种重要的思想方法,它在多项式的化简与求值中应用极为广泛,尝试应用:(1)、把看成一个整体,求出的结果;(2)、已知 , 求的值;(3)、已知 , 求的值.
-
9、某校甲、乙、丙三位同学给希望工程捐款,已知甲同学捐款元,乙同学的捐款金额比甲同学捐款金额的3倍少8元,丙同学的捐款金额是甲、乙两同学捐款总金额的 ,(1)、求甲、乙、丙三位同学的捐款总金额.(用含的代数式表示)(2)、若甲同学捐款为10元,那么三位同学一共捐款多少元?
-
10、长方形场地的长为a米,宽为b米,其内部有两个半圆,如图所示.

(1)求阴影图形的面积;(结果保留);
(2)若a=30,b=18,则阴影图形的面积是多少?(结果保留)
-
11、已知代数式 , .(1)、化简;(2)、当 , 时,求的值;
-
12、已知、互为相反数,、互为倒数,的绝对值是3,试求的值.
-
13、先化简,再代入求值. , 其中 , .
-
14、如图是一个正方体的展开图,将其折叠成正方体后,其中各相对面上的数字之和均相等.
 (1)、______,______.(2)、在(1)的条件下,求的值.
(1)、______,______.(2)、在(1)的条件下,求的值. -
15、合并同类项:(1)、;(2)、;(3)、;
-
16、计算:(1)、;(2)、(3)、(4)、;
-
17、如图所示的程序框图,如图所示的运算程序中,若开始输入的值为100,我们发现第1次输出的结果为50,第2次输出的结果为25,…,第2025次输出的结果为 .

-
18、对任意有理数、定义新运算“”如下: . 则 .
-
19、某班有女生a人,男生比女生的2倍少5人,则男生有人.
-
20、在数轴上,点A表示的数是 , 与A距离3个单位长度的点表示的数是 .