-
1、用配方法解一元二次方程时可配方得( )A、 B、 C、 D、
-
2、如图,在平面直角坐标系中,直线分别与轴、轴交于点、 .
 (1)、求直线的解析式;(2)、求;(3)、若点C在轴上且为等腰三角形,请直接写出所有满足条件的点的坐标.
(1)、求直线的解析式;(2)、求;(3)、若点C在轴上且为等腰三角形,请直接写出所有满足条件的点的坐标. -
3、汽车油箱中有汽油 , 如果不再加油,那么油箱中的油量(单位)随行驶里程(单位:)的增加而减少,平均耗油量为 .(1)、写出表示与的函数解析式(直接写出自变量的取值范围);(2)、当汽车行驶时,油箱中还有多少升()油?(3)、若汽车要行驶 , 那么油箱中的油是否够用?若不够用,中途还需加多少升汽油?
-
4、如图所示,在直角坐标系中, .
 (1)、作出关于轴的对称图形;(2)、写出的顶点坐标;(3)、求出的面积.
(1)、作出关于轴的对称图形;(2)、写出的顶点坐标;(3)、求出的面积. -
5、计算下列各式:(1)、(2)、(3)、
-
6、小明在数轴上先作边长为1的正方形,再用圆规画出了点A(如图所示),则点A所表示的数为 .

-
7、某校有4名教师与若干名学生去看电影,电影票原价为成人每张30元,学生每张15元.现全部打8折.则打折后付款总金额y(元)与学生人数x(人)之间的函数关系式为 .
-
8、若<0,则在平面直角坐标系中,点在第象限.
-
9、若点在一次函数的图象上,则的大小关系是( )A、 B、 C、 D、
-
10、如图,一次函数与x轴的交点为P,则关于x的一元一次方程的解为( )
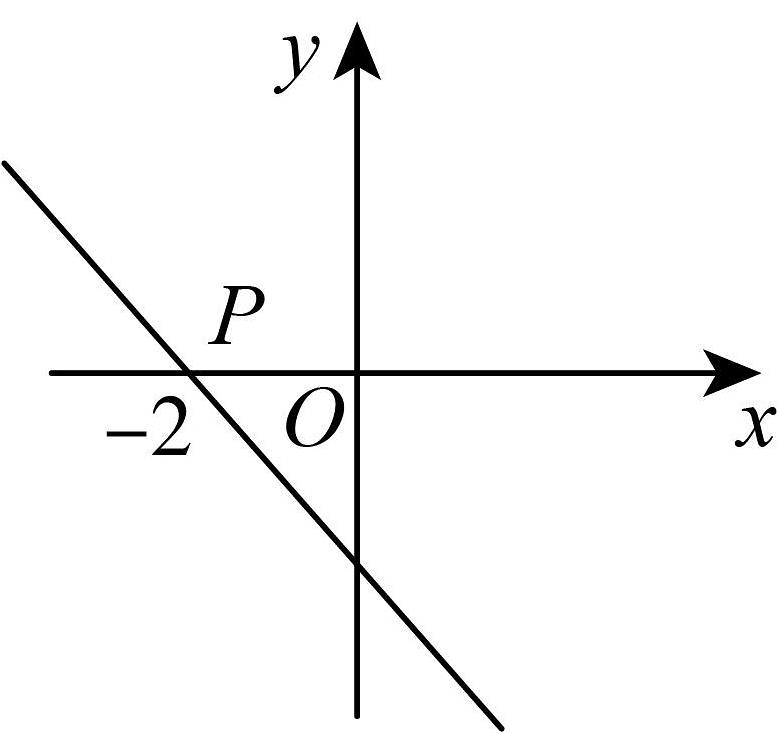 A、-2 B、2 C、3 D、-1
A、-2 B、2 C、3 D、-1 -
11、正比例函数的函数值y随着x增大而增大,则一次函数的图象大致是( )A、
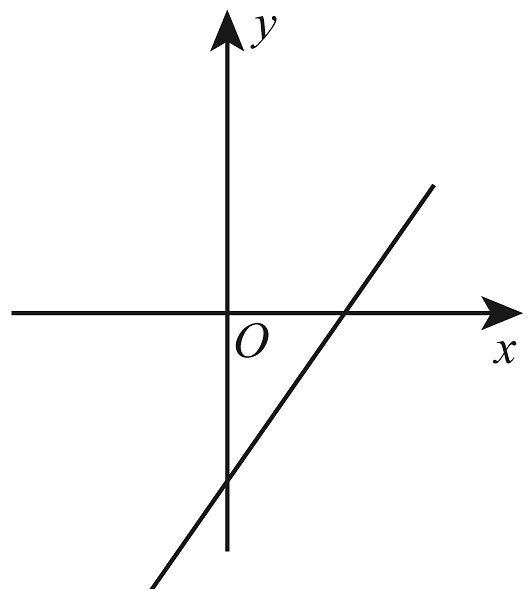 B、
B、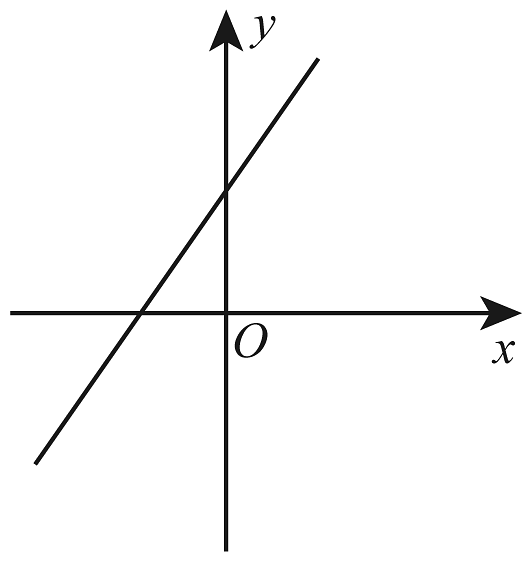 C、
C、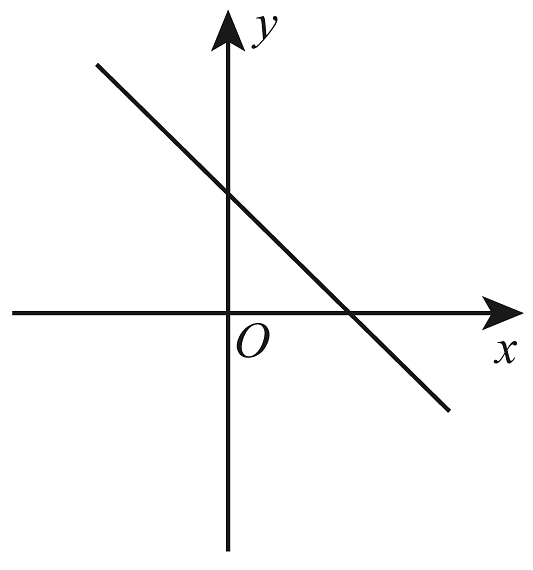 D、
D、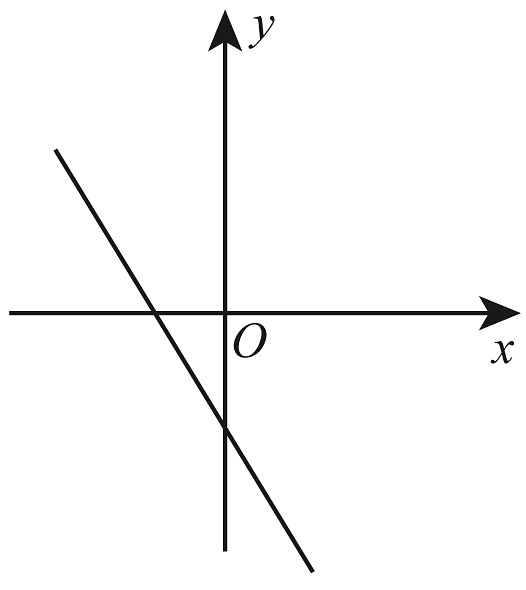
-
12、如图,部分围棋棋盘在某平面直角坐标系内,黑棋(甲)的坐标为 , 则白棋(甲)的坐标为( )
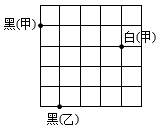 A、 B、 C、 D、
A、 B、 C、 D、 -
13、以下列三个数为边长的三角形中,能构成直角三角形的是( )A、1,2,3 B、2,3,4 C、6,8,10 D、9,16,25
-
14、如图,在平面直角坐标系中,一次函数的图象经过点 , 且与轴相交于点 , 与轴交于点 , 与正比例函数的图象相交于点 , 点的横坐标为1.
 (1)、求一次函数的函数解析式;(2)、不等式的解集是________;(3)、为直线上一点,过点作轴的平行线交于点 , 当时,求点的坐标.
(1)、求一次函数的函数解析式;(2)、不等式的解集是________;(3)、为直线上一点,过点作轴的平行线交于点 , 当时,求点的坐标. -
15、在平面直角坐标系中,一条直线经过 , , 三点.(1)、求a的值.(2)、设这条直线与y轴相交于点D,求的面积.
-
16、已知一次函数 , 其中 .
(1)若点都在该一次函数的图象上,则 .
(2)当时,函数有最大值为2,则函数表达式为 .
-
17、已知平面直角坐标系上的动点A(x,y),满足x=1+2a,y=1﹣a,其中﹣2≤a≤3,有下列四个结论:①﹣3≤x≤7 ②﹣2≤y≤0 ③0≤x+y≤5 ④若x≤0,则0≤y≤3.其中正确的结论是( )A、①③ B、①② C、②④ D、③④
-
18、下列长度的三条线段不能组成三角形的是:( )A、2,3,4 B、4,5,8 C、6,8,10 D、5,5,10
-
19、完全平方公式:适当的变形,可以解决很多的数学问题.
例如:若 , , 求的值.
解:因为 , , 所以 ,
所以;得
根据上面的解题思路与方法,解决下列问题:
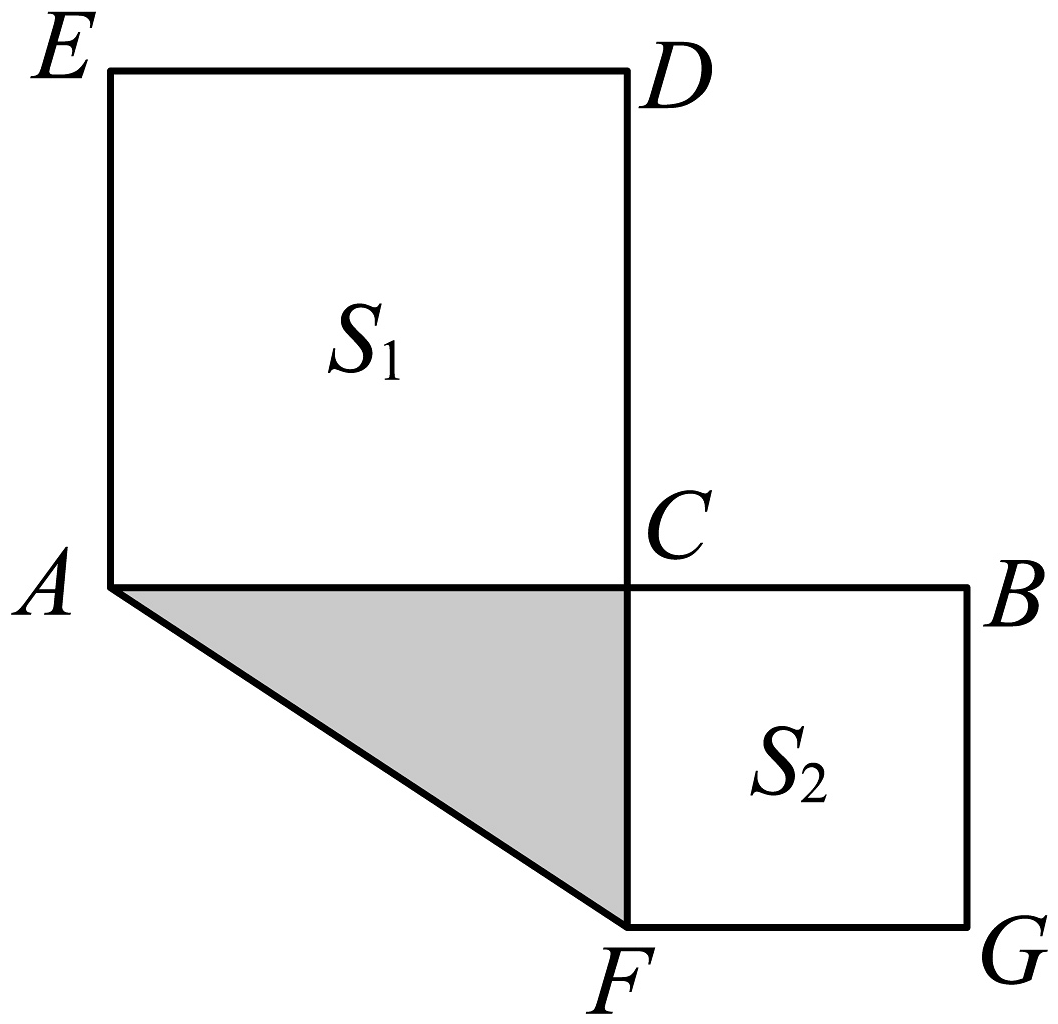 (1)、若 , , 求的值;(2)、请直接写出下列问题答案:
(1)、若 , , 求的值;(2)、请直接写出下列问题答案:①若 , , 则_____;
②若 , 则_____.
(3)、如图,点是线段上的一点,以 , 为边向两边作正方形,设 , 两正方形的面积和 , 求图中阴影部分面积. -
20、如图,这是一张长方形纸片 , 其中 , , 是边上的一点,且 , , 点以的速度从点开始沿的方向运动一周停止,当是以为腰的等腰三角形时,求点运动的时间.
