-
1、我国是最早了解勾股定理的国家之一,它被记载于我国古代著名的数学著作《周髀算经》中.下列各组数中,是“勾股数”的是( )A、7,8,9 B、4,5,6 C、5,12,13 D、8,9,10
-
2、综合与实践
如图1,这个图案是3世纪我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,受这幅图的启发,数学兴趣小组建立了“一线三直角模型”.如图2,在中, , 将线段绕点B顺时针旋转得到线段 , 作交的延长线于点E.
 (1)、【观察感知】
(1)、【观察感知】
如图2,通过观察,线段与的数量关系是;(2)、【问题解决】
如图3,连接并延长交的延长线于点F,若 , , 求的面积;(3)、【类比迁移】
在(2)的条件下,连接交于点N,则;(4)、【拓展延伸】
在(2)的条件下,在直线上找点P,使 , 请直接写出线段的长度. -
3、阅读下列材料,并完成相应学习任务:
古希腊著名的毕达哥拉斯学派发现,一定数目的点或圆在等距离排列下可以形成一个等边三角形,他们把这样的数称之为三角形数.如用1,3,6,10,15,21,…数目的石子就可以排成如图1所示的等边三角形,因而这样的数就是三角形数.所有的三角形数都具有如图2所示的规律.

学习任务:请用一元二次方程的有关知识,解决下列问题:
(1)、根据此规律可知第个三角形数是____________;(用含的代数式表示)(2)、请判断是第几个三角形数?写出解答过程;(3)、若相邻两个三角形数的和是 , 则这两个三角形数分别是多少?请直接写出结果. -
4、已知关于x的一元二次方程 .(1)、求证:方程有两个不相等的实数根;(2)、若的两边 , 的长是这个方程的两个实数根,第三边的长为5,
①若时,请判断的形状并说明理由;
②若是等腰三角形,求等腰三角形的周长.
-
5、如图6个大小相同的小正方形,恰好放置在三角形中,若小正方形的边长为1,则:(1);(2) .

-
6、关于x的方程 , 下列解法完全正确的是( )
甲
乙
丙
丁
两边同时除以得到 .
移项得:
,
∴ ,
∴或 ,
∴ , .
整理得
∵ , , ,
∴
∴
∴ , .
整理得
配方得:
,
∴ ,
∴ ,
∴ , .
A、甲和乙 B、乙和丙 C、乙和丁 D、甲和丁 -
7、如图,为了测量山坡护坡石坝的坡度(坡面的铅垂高度与水平宽度的比称为坡度),把一根长的竹竿斜靠在石坝旁,量出杆长处的点离地面的高度 , 又量得杆底与坝脚的距离 , 则石坝的坡度为( )
 A、 B、3 C、 D、4
A、 B、3 C、 D、4 -
8、如图、在中, , , 点P从A开始沿边向点B以2个单位秒的速度移动,点Q从点B开始沿边向点C以4个单位秒的速度移动,如果P、Q分别同时出发,经过( )秒后,与相似.
 A、2 B、 C、或2 D、或2
A、2 B、 C、或2 D、或2 -
9、在图(1)、(2)所示的△ABC中,AB=4,AC=6.将△ABC分别按照图中所标注的数据进行裁剪,对于各图中剪下的两个阴影三角形而言,下列说法正确的是( )
 A、只有(1)中的与△ABC相似 B、只有(2)中的与△ABC相似 C、都与△ABC相似 D、都与△ABC不相似
A、只有(1)中的与△ABC相似 B、只有(2)中的与△ABC相似 C、都与△ABC相似 D、都与△ABC不相似 -
10、用配方法解方程时,配方后正确的是( )A、 B、 C、 D、
-
11、已知线段b是线段、c的比例中项,且 , 那么b:c的值是( )A、 B、 C、 D、
-
12、如图,在中, , , , 则等于( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
13、如图,在中, , 点P从点C出发,以每秒3个单位长度的速度沿折线运动.设点P的运动时间为 .
 (1)、 .(2)、求斜边上的高线长.(3)、①当P在上时,的长为 , t的取值范围是 . (用含t的代数式表示)
(1)、 .(2)、求斜边上的高线长.(3)、①当P在上时,的长为 , t的取值范围是 . (用含t的代数式表示)②若点P在的角平分线上,则t的值为 .
(4)、在整个运动过程中,直接写出是以为一腰的等腰三角形时t的值. -
14、如图,在中,于点 , 于点 .
 (1)、如图1,若 , 求证:;(2)、如图2,点为边上的中点,连接、、 , 试判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 求的周长.
(1)、如图1,若 , 求证:;(2)、如图2,点为边上的中点,连接、、 , 试判断的形状,并说明理由;(3)、在(2)的条件下,若 , , 求的周长. -
15、已知:方格纸中的每个小方格都是边长为个单位的正方形,在建立平面直角坐标系后,的顶点均在格点上,点的坐标为 .
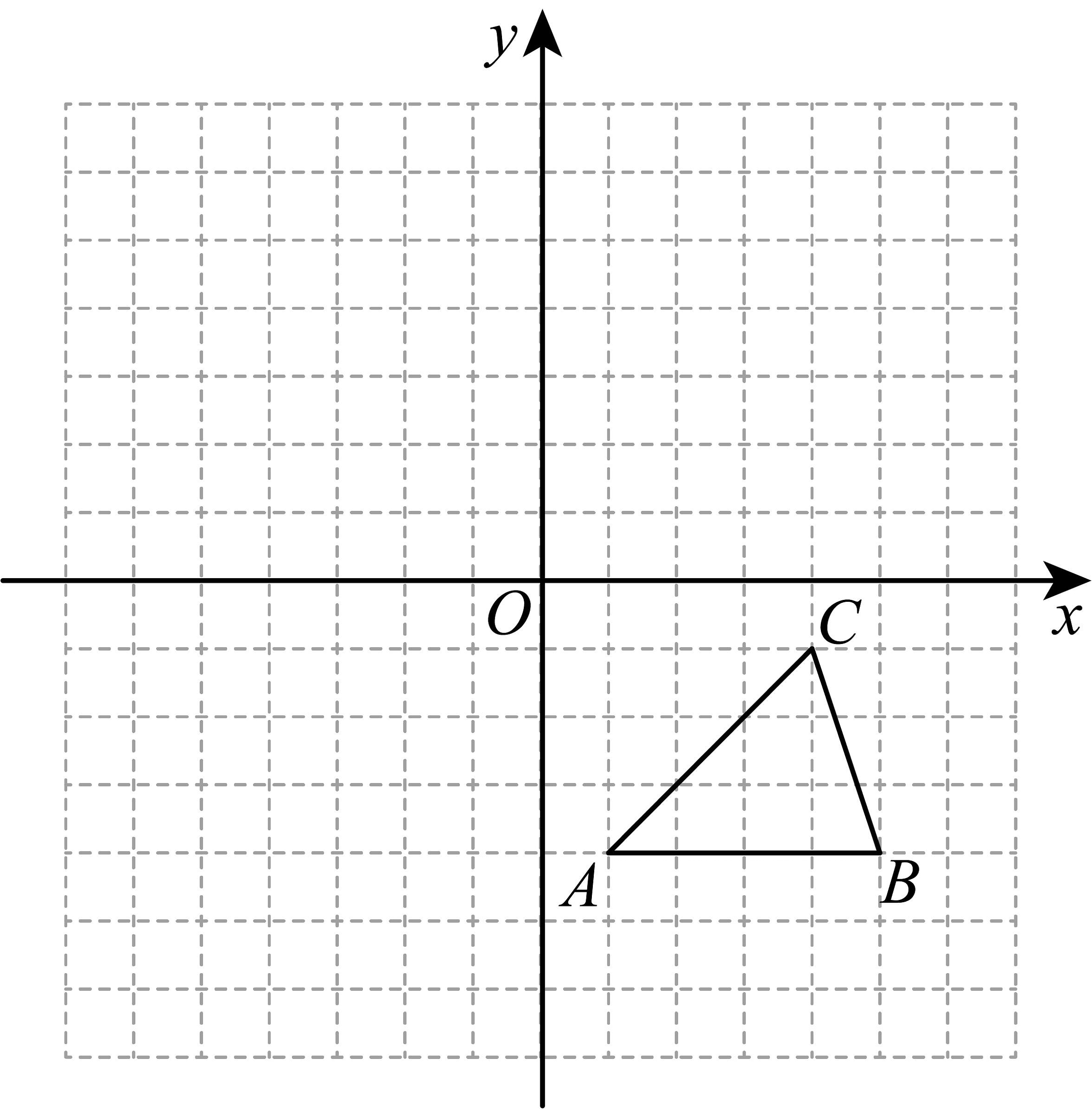 (1)、请以轴为对称轴,画出与对称的;(2)、点与点关于轴对称,则 , .(3)、如果要使与全等,那么点的坐标是 .
(1)、请以轴为对称轴,画出与对称的;(2)、点与点关于轴对称,则 , .(3)、如果要使与全等,那么点的坐标是 . -
16、解下列不等式(组),并在数轴上表示出来:(1)、;(2)、 .
-
17、将点向左平移2个单位,向下平移3个单位,后得到点 , 则平移后点的坐标 .
-
18、下列命题中,是假命题的是( )A、直角三角形的两个锐角互余 B、全等三角形的对应边相等 C、两边及其中一边的对角分别相等的两个三角形全等 D、对顶角相等
-
19、如图1是一座圆弧型拱桥侧面示意图.水面宽与桥长均为24米,桥拱顶部离水面的距离为8米,以桥拱顶部为原点,桥面为x轴建立平面直角坐标系.
 (1)、求圆弧型桥拱所在圆的半径;(2)、如图2,桥面上方有3根高度均为4米的支柱 , , , 过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面的距离为1米.
(1)、求圆弧型桥拱所在圆的半径;(2)、如图2,桥面上方有3根高度均为4米的支柱 , , , 过相邻两根支柱顶端的钢缆呈形状相同的抛物线,其最低点到桥面的距离为1米.①求出轴右侧一条钢缆抛物线的函数表达式;
②为庆祝节日,在钢缆和桥拱之间竖直装饰若干条彩带,求经过钢缆最低点的彩带的长度.
-
20、如图,在中, , , 是上一动点,连接 , 以为直径的交于点 , 连接并延长交于点 , 交于点 , 连接 .
 (1)、求证:点在上.(2)、当点移动到使时,求的值.(3)、当点到移动到使时,求证: .
(1)、求证:点在上.(2)、当点移动到使时,求的值.(3)、当点到移动到使时,求证: .