-
1、已知为实数,规定运算: , . 按上述规定,当时,的值等于( )A、 B、 C、 D、0
-
2、根据图中的程序,当输入为时,输出的值是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
3、若 , , , 则a , b , c的大小关系为( )A、 B、 C、 D、
-
4、已知分别是的整数部分和小数部分,那么的值是( )A、 B、 C、2 D、5
-
5、大自然是美的设计师,即使是一片小小的树叶,也蕴含着“美学”.如图,的值接近黄金比 , 则下列估算正确的是( )
 A、 B、 C、 D、
A、 B、 C、 D、 -
6、如果 , 则的值为( )A、 B、1 C、2 D、
-
7、已知的平方根是 , 是的立方根,则的值是( )A、 B、 C、 D、
-
8、化简的值为( )A、 B、 C、 D、
-
9、下列各数中,是无理数的是( )A、 B、 C、 D、3.1415926
-
10、已知两条平行线 , , 一块直角三角尺 , 且点不可能同时落在直线和之间.
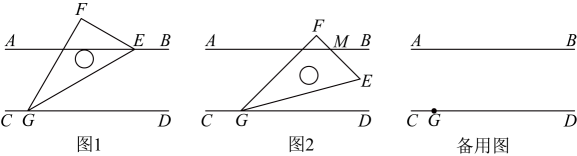 (1)、如图1,把三角尺的顶点分别放在上,若 , 则的度数为;(2)、如图2,把三角尺的锐角顶点放在上,且保持不动,若点恰好落在和之间,且与线段交于点 , 若 , 求的度数;(3)、把三角尺的锐角顶点放在上,且保持不动,旋转三角尺,若存在 , 请直接写出射线与所夹锐角的度数.
(1)、如图1,把三角尺的顶点分别放在上,若 , 则的度数为;(2)、如图2,把三角尺的锐角顶点放在上,且保持不动,若点恰好落在和之间,且与线段交于点 , 若 , 求的度数;(3)、把三角尺的锐角顶点放在上,且保持不动,旋转三角尺,若存在 , 请直接写出射线与所夹锐角的度数. -
11、如图,已知 , , .
 (1)、求证:;(2)、试求出的度数
(1)、求证:;(2)、试求出的度数 -
12、如图(1), , 平分 .
 (1)、如果 , 求的度数;(2)、反向延长射线得 , 如图(2),若 , 求的度数.
(1)、如果 , 求的度数;(2)、反向延长射线得 , 如图(2),若 , 求的度数. -
13、已知:如图,于M , 于N , .
 (1)、求证:;(2)、若 , , 求的度数.
(1)、求证:;(2)、若 , , 求的度数. -
14、把下面解答过程补充完整.如图, .
 (1)、试说明;
(1)、试说明;说明:∵(已知),
∴().
又∵(已知),
∴(等量代换),
∴().
(2)、与的位置关系如何?为什么?解:与的位置关系是 , 理由如下:
∵(已知),
∴(两直线平行,内错角相等).
又∵(已知),
∴(等量代换),
∴().
-
15、如图,直线 与 相交于点 , 射线 平分 , 射线 在 内.
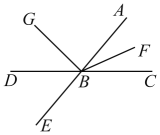 (1)、若 的补角是它的余角的 倍,求 的度数;(2)、在(1)的条件下,若 , 求 的度数.
(1)、若 的补角是它的余角的 倍,求 的度数;(2)、在(1)的条件下,若 , 求 的度数. -
16、如图,线段和表示两面镜子,且直线直线 , 光线经过镜子反射到镜子 , 最后反射到光线光线反射时, , , 下列结论:
直线直线;
的角平分线所在的直线垂直于直线;
如果 , 那么;
当直线绕点顺时针旋转 , 直线绕点顺时针旋转时,直线与直线不平行.
其中正确的是 .

-
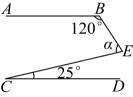
17、如图, , , , 则的度数为°.
-
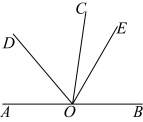
18、如图,点在直线上,平分 , , , 则 .
-
19、如图,与交于点 , 点在直线上,交于点 , , , , 给出下列四个结论:①;②;③;④ . 上述结论中,所有正确结论的序号是( )
 A、①② B、①②③ C、①②④ D、①②③④
A、①② B、①②③ C、①②④ D、①②③④ -
20、如图, , M是平面内一点,连接MB , MC , 的平分线与的平分线交于点N . 若 , 则的度数为( )
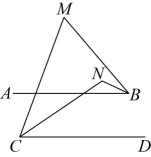 A、30° B、40° C、50° D、60°
A、30° B、40° C、50° D、60°