-
1、如图所示,在Rt△ABC中,∠A=30°,∠ABC=90°,将Rt△ABC绕点B逆时针方向旋转得到△A'BC' , 此时恰好点C在A'C'上,A'B交AC于点E,则△ABE与△ABC的面积之比为( )
 A、1∶2 B、1∶3 C、2∶3 D、3∶4
A、1∶2 B、1∶3 C、2∶3 D、3∶4 -
2、如图所示,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿射线BC的方向平移,得到△A'B'C' , 再将△A'B'C' 绕点A'逆时针旋转一定角度,点B'恰好与点C重合,则平移的距离和旋转角的度数分别为( )
 A、4,30° B、2,60° C、1,30° D、3,60°
A、4,30° B、2,60° C、1,30° D、3,60° -
3、如图所示,正方形OABC的两边OA,OC分别在x轴、y轴上,点D(5,3)在边AB上,以点C为中心,把△CDB旋转90°,则旋转后点D的对应点D'的坐标是( )
 A、(2,10) B、(-2,0) C、(2,10)或(-2,0) D、(10,2)或(-2,0)
A、(2,10) B、(-2,0) C、(2,10)或(-2,0) D、(10,2)或(-2,0) -
4、如图所示,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,当∠EPF在△ABC内绕点P旋转时,下列结论错误的是( )
 A、EF=AP B、△EPF为等腰直角三角形 C、AE=CF D、S四边形AEPF=S△ABC
A、EF=AP B、△EPF为等腰直角三角形 C、AE=CF D、S四边形AEPF=S△ABC -
5、如图所示,在△ABC中,∠A=30°,将△ABC绕着点B逆时针旋转40°到△DBE的位置,则∠α的度数是( )
 A、70° B、60° C、80° D、65°
A、70° B、60° C、80° D、65° -
6、在平面直角坐标系xOy中,与点P(2x-1,x+3)关于原点成中心对称的点在第四象限内,则x的取值范围是( )A、x< B、-3<x< C、x> D、x>-3
-
7、如图所示,在平面直角坐标系中,点B,C,E在y轴上,点C的坐标为(0,1),AC=2,Rt△ODE是Rt△ABC经过某些变换得到的,则正确的变换是( )
 A、△ABC绕点C逆时针旋转90°,再向下平移1个单位长度 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位长度 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位长度 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位长度
A、△ABC绕点C逆时针旋转90°,再向下平移1个单位长度 B、△ABC绕点C顺时针旋转90°,再向下平移1个单位长度 C、△ABC绕点C逆时针旋转90°,再向下平移3个单位长度 D、△ABC绕点C顺时针旋转90°,再向下平移3个单位长度 -
8、某校区2号楼楼梯的示意图如图所示,现在要在楼梯上铺一条地毯,如果楼梯的宽度是1.8 m,那么地毯的面积为( )
 A、(a+1.8)h m2 B、(h+1.8)a m2 C、1.8(h+a)m2 D、1.8ah m2
A、(a+1.8)h m2 B、(h+1.8)a m2 C、1.8(h+a)m2 D、1.8ah m2 -
9、将如图所示的图形绕其中心旋转某一角度后会与原图形重合,这个角度不能是( )
 A、90° B、120° C、180° D、270°
A、90° B、120° C、180° D、270° -
10、下列4个富有民族特色的窗户图形中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、
-
11、综合与实践:
【问题情境】在数学实践课上,老师让小组合作探究两个完全相同的含 角的三角板拼图间存在的关系.
如图,已知 , , ,.

【操作探究】
(1)、 如图①,当点 , , 在同一条直线上时,直线与直线的位置关系是;(2)、 如图②,将图①中的三角板绕点顺时针旋转 ,边与边交于点 , 请判断此时与的位置关系及的形状,并说明理由;(3)、 如图③,将图①中的三角板绕着点顺时针旋转,边与边交于点 , 当是以为腰的等腰三角形时,求的长. -
12、已知 , 点 , 分别在射线 , 上,将线段绕点顺时针旋转 得到线段 , 过点作的垂线交射线于点.
 (1)、 如图①,当点在射线上时,求证:是的中点;(2)、 如图②,当点在内部时,作 , 交射线于点 , 用等式表示线段与的数量关系,并证明.
(1)、 如图①,当点在射线上时,求证:是的中点;(2)、 如图②,当点在内部时,作 , 交射线于点 , 用等式表示线段与的数量关系,并证明. -
13、已知是等腰直角三角形, ,点是所在平面内任意一点,绕点逆时针旋转 得到 , 连接 , , .
 (1)、 如图①,若点为内一点,求证:;(2)、 如图②,若点为边上一点, , , 求的长.
(1)、 如图①,若点为内一点,求证:;(2)、 如图②,若点为边上一点, , , 求的长. -
14、在平面直角坐标系中,的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
 (1)、 若和关于原点成中心对称,画出;(2)、 将绕点顺时针旋转 ,画出旋转后得到的 , 并写出点的坐标;(3)、 若在轴上存在一点 , 满足点到点与点的距离之和最小,请写出的最小值为.
(1)、 若和关于原点成中心对称,画出;(2)、 将绕点顺时针旋转 ,画出旋转后得到的 , 并写出点的坐标;(3)、 若在轴上存在一点 , 满足点到点与点的距离之和最小,请写出的最小值为. -
15、如图,在直角三角形中, , ,将三角形沿方向平移得到三角形.
 (1)、 求的度数;(2)、 若 , , 求的长.
(1)、 求的度数;(2)、 若 , , 求的长. -
16、如图,已知的顶点 , , .若向右平移4个单位长度,再向下平移3个单位长度得到 , 且点 , , 的对应点分别是 , , .
 (1)、 画出 , 并直接写出点的坐标;(2)、 若内有一点经过以上平移后的对应点为 , 直接写出点的坐标.
(1)、 画出 , 并直接写出点的坐标;(2)、 若内有一点经过以上平移后的对应点为 , 直接写出点的坐标. -
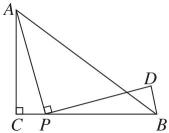
17、如图,在中, , , , 点是线段上的动点,连接 , 将线段绕点顺时针旋转 得到线段 , 连接 , 则的最小值是 .
-
18、如图,在平面直角坐标系中,点的坐标为 , 点在第一象限内,将沿轴正方向平移得到 , 若点的对应点在直线上,则点与其对应点之间的距离为.

-
19、如图,正方形内的图形来自中国古代的太极图,圆中的黑色部分和白色部分关于正方形的中心成中心对称,设黑色部分的面积为 , 正方形的边长为2,则 .

-
20、麒麟水乡景区是国家级景区,是集田园风光和水乡风情为一体的旅游景区,盛夏的麒麟水乡秀丽端庄,千亩荷花在微风中飘曳,为了便于游客领略“人从桥上过,如在河中行”的美好意境,景区工作人员拟在如图所示的长方形荷塘上架设小桥,桥宽度忽略不计,若荷塘的长为90米,宽为50米,则小桥总长为.
