相关试卷
-
1、已知函数 .(1)、求在上的单调递增区间;(2)、已知的内角A,B,C的对边长分别是a,b,c,若 , , 求面积的最大值,及此时a、b的值.
-
2、如图,正四棱柱中, , 点E在上且 .
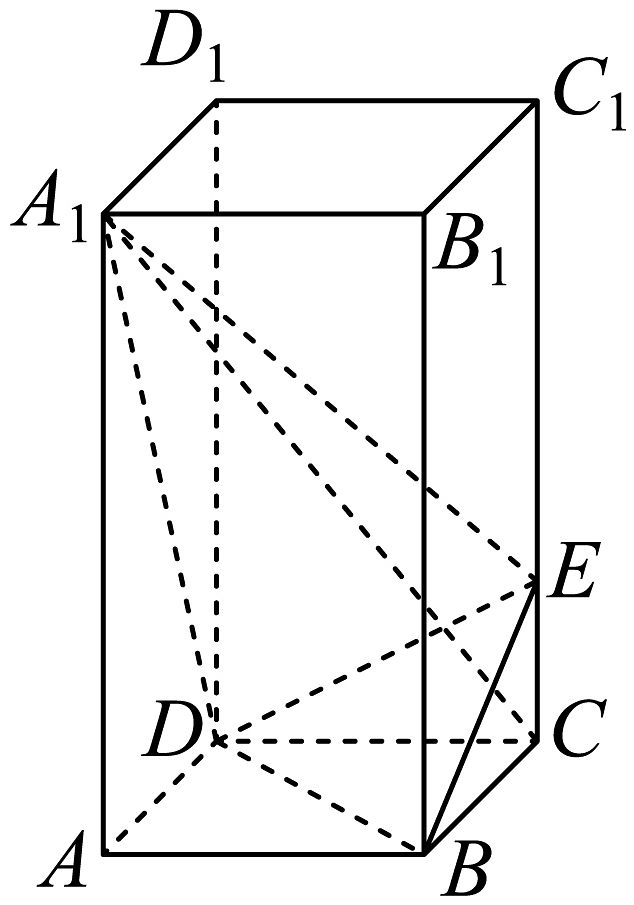 (1)、证明:;(2)、求点B到平面的距离;(3)、求直线与平面所成角的正弦值.
(1)、证明:;(2)、求点B到平面的距离;(3)、求直线与平面所成角的正弦值. -
3、(1)一条光线从点射出,遇反射,反射光线所在直线的倾斜角为 , 若 , 求反射光线所在直线方程;
(2)的三个顶点分别是 , , , 求的外接圆的方程.
-
4、在四面体ABCD中, , , , M,N分别为棱AB,CD所在直线的点,则线段长度的最小值为 .
-
5、已知空间5个点A,B,C,D,P,且A,B,C,D共面,若且 , , 则的最小值为 .
-
6、已知直线l的方程为 , 则直线l过定点.
-
7、在空间直角坐标系中,已知向量 , 点 , 点 .
(1)若直线l经过点 , 且以方向向量,P是直线l上的任意一点,则直线l的方程为;
(2)若平面经过最 , 且以为法向量,P是平面内的任意一点,则平面的方程为 .
如图,一在棱长为1的正方体中,以O为坐标原点,建立如图所示的空间直角坐标系,则下列说法正确的是( )
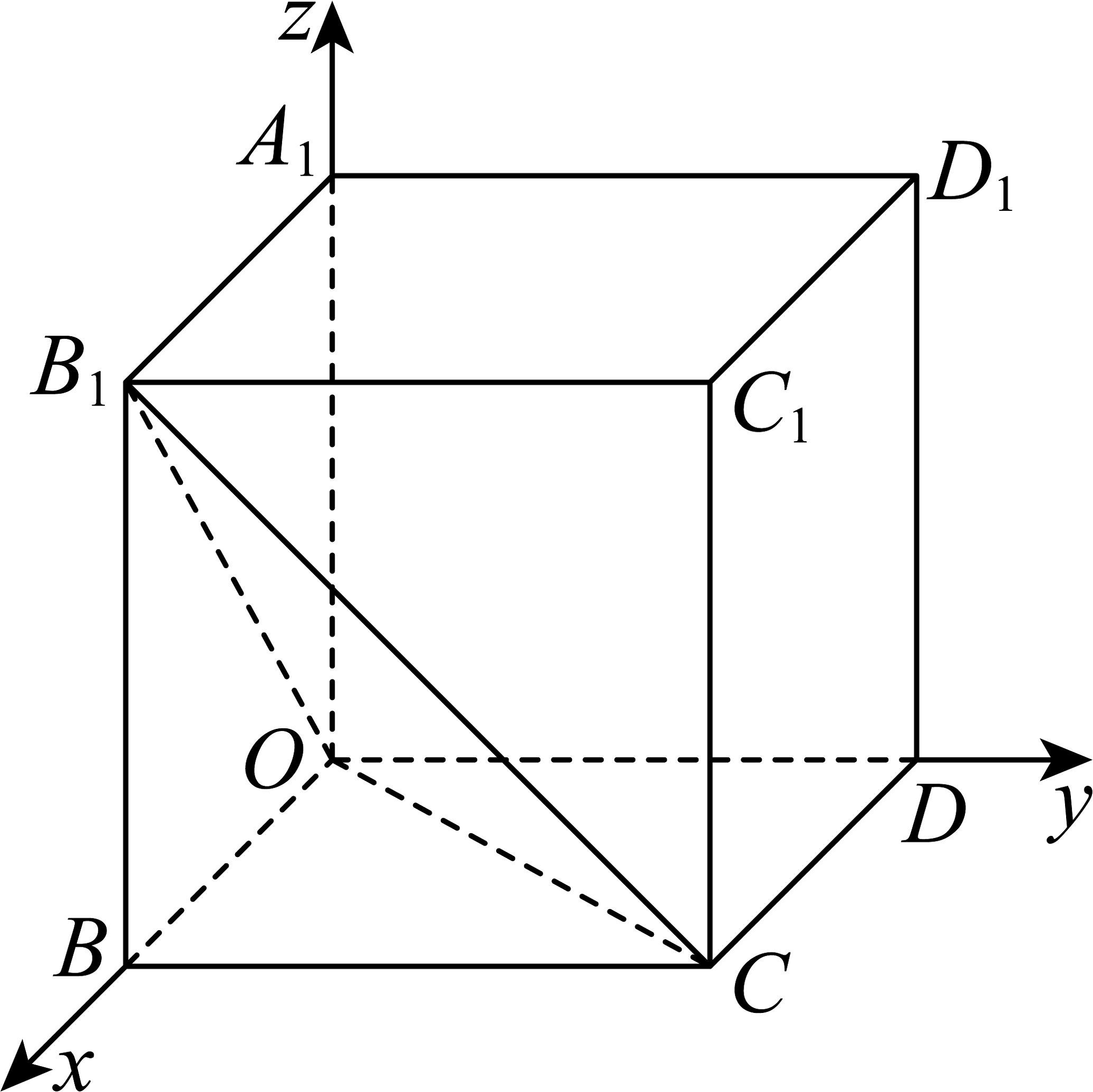 A、平面的法向量为 B、直线的方程为 C、过点的平面方程为 , 则平面截正方体所得截面的面积为 D、平面方程为 , 平面方程为 , 则平面与平面之间的距离为
A、平面的法向量为 B、直线的方程为 C、过点的平面方程为 , 则平面截正方体所得截面的面积为 D、平面方程为 , 平面方程为 , 则平面与平面之间的距离为 -
8、已知直线和为函数()图象上两条相邻的对称轴.则下列说法正确的是( )A、 B、 C、若 , 则图象可以由图象向左平移个单位得到 D、若 , 则在区间上的值域为
-
9、在中,角A,B,C所对的边分别为a,b,c,则下列条件能确定2个三角形的是( )A、 , , B、 , , C、 , , D、 , ,
-
10、函数 , 若关于x的方程有三个不同的实数根,则实数m的取值范围是( )A、 B、 C、 D、
-
11、已知实数x,y满足 , 且 , 则不可能是( )A、-3 B、-4 C、3 D、4
-
12、已知函数在R上单调递增,则a的取值范围是( )A、 B、 C、 D、
-
13、直线l:(参数,)的倾斜角的取值范围是( )A、 B、 C、 D、
-
14、已知一组数据的平均数 , 方差 , 则数据的平均数、方差分别为( )A、16,20 B、16,80 C、18,20 D、18,80
-
15、下列结论中,错误的结论有( )A、取得最大值时的值为 B、若 , 则的最大值为 C、函数的最小值为 D、若 , , 且 , 那么的最小值为
-
16、高一共50名学生参加100米和400米两项体育测试并且每人至少有一项合格,100米和400米两项测试成绩合格的分别有29人和25人,则这两项成绩都合格的人数是( )A、3 B、4 C、5 D、9
-
17、若为定义在上的函数,且关于原点对称,则“存在 , 使得”是“函数为非奇非偶函数”的( )A、充分不必要条件 B、必要不充分条件 C、充分必要条件 D、既不充分也不必要条件
-
18、对于数列 , 如果存在正整数 , 当任意正整数时均有 , 则称为的“项递增相伴数列”.若可取任意的正整数,则称为的“无限递增相伴数列”.(1)、已知 , 请写出一个数列的“无限递增相伴数列”,并说明理由?(2)、若满足 , 其中是首项的等差数列,当为的“无限递增相伴数列”时,求的通项公式:(3)、已知等差数列和正整数等比数列满足: , 其中k是正整数,求证:存在正整数k,使得为的“2024项递增相伴数列”.
-
19、已知函数.(1)、若函数在处切线的斜率为 , 求实数的值;(2)、当时,恒成立,求实数的最大值;(3)、当时,证明:
-
20、如图1,在五边形中, , , 且 , 将沿折成图2,使得 , 为的中点.
 (1)、证明:平面;(2)、若与平面所成的角为 , 求二面角的正弦值.
(1)、证明:平面;(2)、若与平面所成的角为 , 求二面角的正弦值.